从公式详解相位滞后指数（Phase-Lag Index, PLI）、加权相位滞后指数 wPLI

一、什么是相位滞后指数？

PLI是基于相位滞后的连通性方法，该方法告诉我们（以下是我看到的两种不同解释）：

1. 某一时刻（timePoint）不同试验（trial）收集到的两个信号的相角差在复平面的投影是否始终指向同一侧（虚轴的正侧 或 虚轴的负侧）。（这个与PLV的计算有点类似）
2. 某一段时间内（timePeriod）收集到的 两个信号的相角差 在复平面的投影是否始终指向同一侧（虚轴的正侧 或 虚轴的负侧）。
   PLI可以忽略由体积效应引起的0和pi的相角差。

二、为什么要忽略0和pi的相角差？

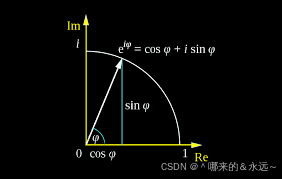
三、复平面上的相位差

四、PLI的计算

五、MATLAB实现PLI

function PLI = PhaseLagIndex(X, trialTimePoint, timePeriod)
    %% Given a multivariate data, returns phase lag index matrix
    % trialTimePoint and timePeriod decide which PLI to perform.
    % trialTimePoint and timePeriod are both 0 or 1，select timePeriod.
    % Modified the mfile of 'phase synchronization'
    % X: channel * timePoint * trial
    if trialTimePoint==1 && timePeriod==1
        trialTimePoint = 0;
    end
    if trialTimePoint==0 && timePeriod==0
        timePeriod = 1;
    end

    numChannels = size(X, 1); 
    numtimePoint = size(X, 2); 
    numTrials = size(X, 3); 

    %% Obtain the instantaneous phase of each channel by Hilbert transform
    dataP = zeros(size(X));
    for channelCount = 1:numChannels
        dataP(channelCount, :, :) = angle(hilbert(squeeze(X(channelCount, :, :))));
    end
    
    % whether the projections of phase angle differences collected from different trials at a given moment always point to the same side in the complex plane
    if trialTimePoint == 1
        %% Calculation of PLI
        PLI = ones(numtimePoint, numChannels, numChannels);
        for ch1 = 1:numChannels-1
            for ch2 = ch1+1:numChannels
                %%%%%% phase lage index
                PDiff = squeeze(dataP(ch1,:,:)) - squeeze(dataP(ch2,:,:));  % hase difference at each time point
                PLI(:,ch1,ch2) = abs(sum(sign(sin(PDiff)), 2)/numTrials);   % only count the asymmetry
                PLI(:,ch2,ch1) = PLI(:,ch1,ch2);
            end
        end
    end
    
    % Whether the projections of the phase angle differences collected in a given time period 
    % always point to the same side of the complex plane 
    % (positive side of the imaginary axis or negative side of the imaginary axis).
    if timePeriod == 1
        % Phase averaging between trials
        phi1 = mean(dataP, 3);
        ch = numChannels;
        %% Calculation of PLI
        PLI = ones(ch,ch);
        for ch1=1:ch-1
            for ch2=ch1+1:ch
                %%%%%% phase lage index
                PDiff=phi1(ch1,:)-phi1(ch2,:); % phase difference
                PLI(ch1,ch2)=abs(mean(sign(sin(PDiff)))); % only count the asymmetry
                PLI(ch2,ch1)=PLI(ch1,ch2);
            end
        end
    end
end

六、计算结果差异

下面是我用这两种方法计算的某一时间区间的PLI，很明显这两个差别很大，我也不晓得哪个才是对的，但我更倾向于第一个，n表示trial的个数。

n表示trial时，要计算某区间的PLI：先计算每一个时刻的PLI，得到所有时刻的PLI后，再对所需的时间区间的PLI取平均。

七、加权相位滞后指数wPLI（weighted Phase-Lag Index）

改进点：尽管 PLI 已经对零滞后交互不敏感，但加权相位滞后指数（weighted PLI）进一步解决了由体积传导（volume conduction）引起的潜在混杂因素。
体积传导问题：体积传导是指脑电信号在头皮上传播时，由于脑组织和头皮的电导率差异，导致信号在不同电极之间传播时出现空间扩散的现象。这种现象可能会导致虚假的信号同步性，从而干扰分析结果。
加权机制：加权 PLI 通过根据角度差与实轴的距离对角度差的贡献进行加权，进一步优化了 PLI 的性能。具体来说，它对那些接近零滞后（“almost-zero-lag”）的交互进行了调整。
“almost-zero-lag”交互：这些交互是指相位差非常接近零的情况，但并不是完全零滞后。加权 PLI 将这些“几乎零滞后”的交互视为噪声，因为它们可能会掩盖真正的零滞后交互。通过加权，这些噪声的贡献被降低，从而更准确地反映真实的信号同步性。

八、python代码实现：某段时间内两个信号的wPLI

import numpy as np
from scipy.signal import hilbert

def calculate_wPLI(signal1, signal2):
    """
    计算两个信号之间的去偏加权相位滞后指数（dwPLI）
    
    参数：
        signal1, signal2: 一维数组，形状为 (n_timepoints,)
    
    返回：
        wPLI: 标量，取值范围 [-1, 1]
        · wPLI ≈ 1：信号1始终领先信号2。
		· wPLI ≈ -1：信号1始终滞后信号2。
		· wPLI ≈ 0：无稳定相位关系。
    """
    # 1. 计算希尔伯特变换，获取解析信号
    analytic_signal1 = hilbert(signal1)
    analytic_signal2 = hilbert(signal2)
    
    # 2. 提取瞬时相位（单位：弧度）
    phase1 = np.angle(analytic_signal1)
    phase2 = np.angle(analytic_signal2)
    
    # 3. 计算相位差的正弦值（虚部）
    phase_diff = phase1 - phase2
    imag_part = np.sin(phase_diff)  # 等价于 np.imag(np.exp(1j * phase_diff))
    
    # 4. 计算加权分子和分母
    numerator = np.mean(np.abs(imag_part) * np.sign(imag_part))
    denominator = np.mean(np.abs(imag_part))
    
    # 5. 计算加权相位滞后指数（wPLI）
    wPLI = numerator / denominator
    return wPLI