完全二叉树的节点数与平衡二叉树、二叉树的所有路径

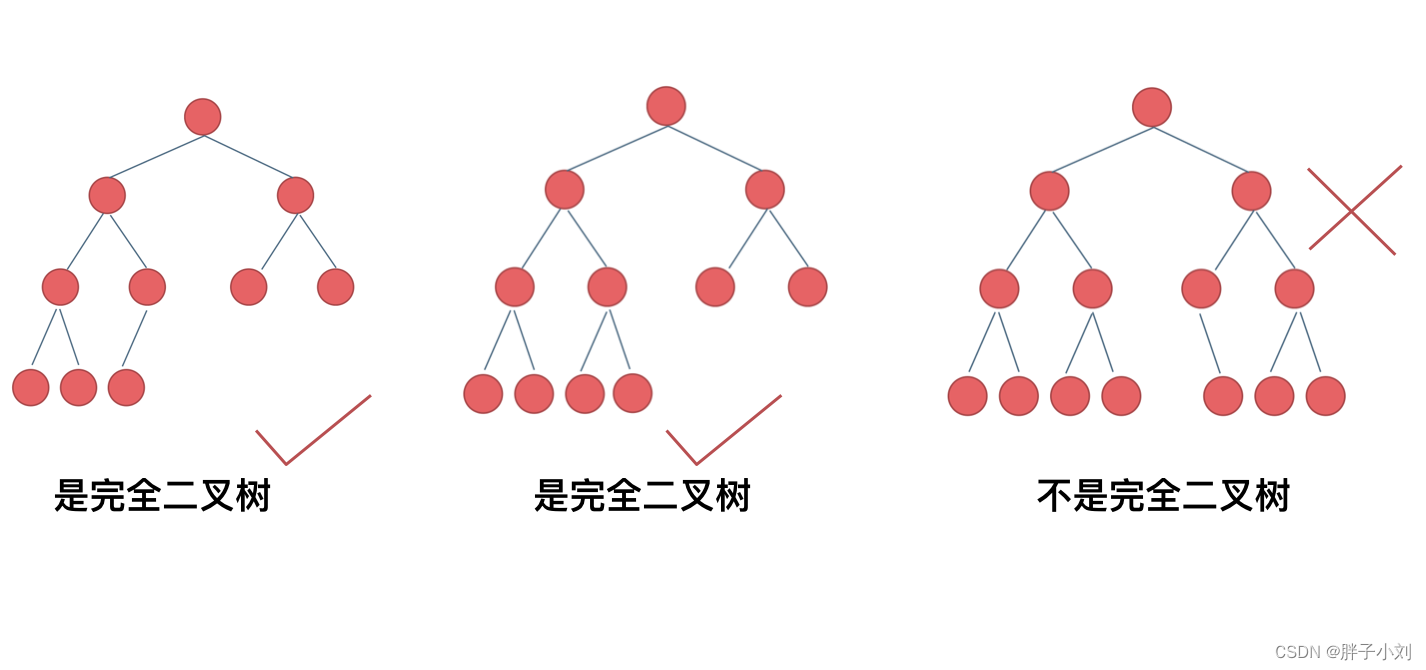
完全二叉树长这个样子
完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

完全二叉树（一）如图： 222.完全二叉树的节点个数

完全二叉树（二）如图： 222.完全二叉树的节点个数1

可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。

递归法

class Solution:
   def countNodes(self,root:TreeNode)->int:
       return self.getNodesNum(root)
   def getNodesNum(self,cur):
       if not cur:
          return 0
       leftNum=self.getNodesNum(cur.left)
       rightNum=self.getNodeNum(cur.right)
       treeNum=leftNum+rightNum+1
       return treeNum

平衡二叉树

一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
这里强调一波概念：

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。
但leetcode中强调的深度和高度很明显是按照节点来计算的，如图：

110.平衡二叉树2

关于根节点的深度究竟是1 还是 0，不同的地方有不一样的标准，leetcode的题目中都是以节点为一度，即根节点深度是1。但维基百科上定义用边为一度，即根节点的深度是0，我们暂时以leetcode为准（毕竟要在这上面刷题）。

因为求深度可以从上到下去查 所以需要前序遍历（中左右），而高度只能从下到上去查，所以只能后序遍历（左右中）

递归法

class Solution:
    def isBalanced(self,root:TreeNode)->bool:
      if self.get_height(root)!=-1:
         return True
      else:
         return False
    
   def get_height(self,root:TreeNode)->int:
     if not root:
        return 0
     if(left_height:=self.get_height(root.left))==-1:
        return -1
     if(right_height:=self.get_height(root.right))==-1:
        return -1
     if abs(left_height-right_height)>1:
        return -1
     else:
        return 1+max(left_height,right_height)

二叉树的所有路径

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

递归法+回溯

class Solution:
   def traversal(self,cur,path,result):
       path.append(cur.val)
       if not cur.left and not cur.right:
         sPath = '->'.join(map(str,path))
         result.append(sPath)
         return
       if cur.left:
         self.traversal(cur.left,path,result)
         path.pop()
       if cur.right:
         self.traversal(cur.right,path,result)
         path.pop()
       
   def binaryTreePaths(self,root):
       result=[]
       path=[]
       if not root:
          return result
       self.traversal(root,path,result)
       return result