淼淼刷力扣

引言

本人初次尝试写博客，希望各位看官大佬多多包容
有错误希望巨巨们提出来，我一定会及时改正，谢谢大家
在自己最好的年纪，找到了未来的目标
还有1年奋斗刷题，明年去面试实习，加油！

题目要求：

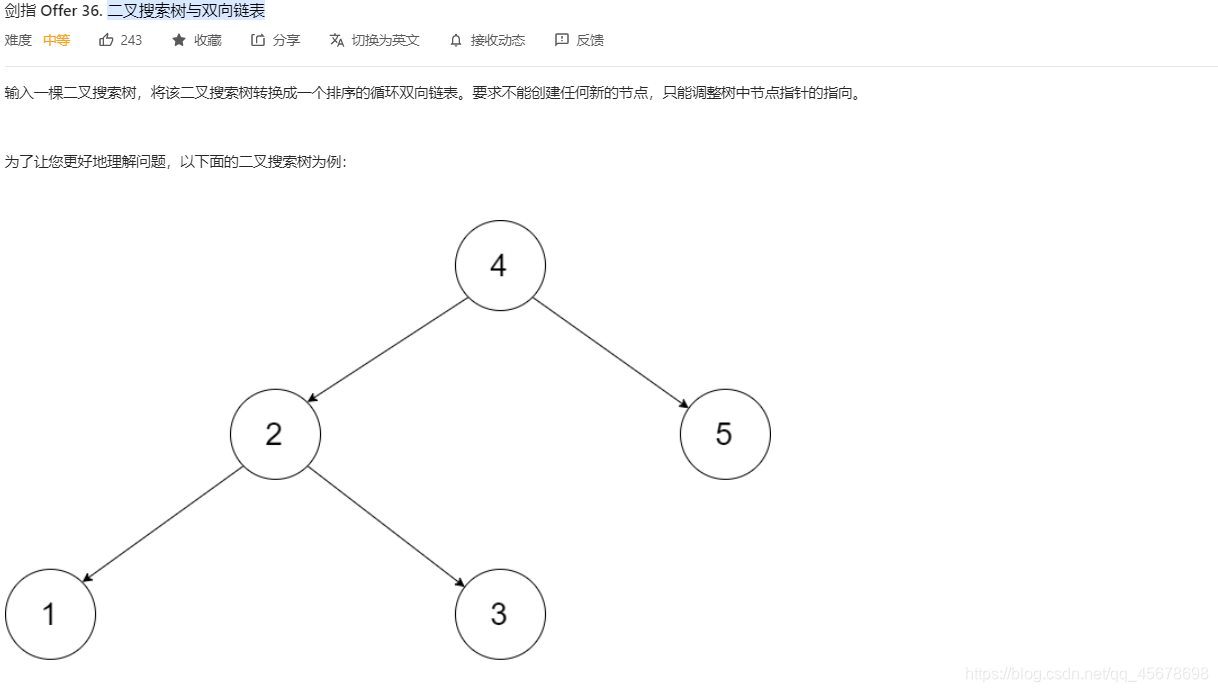
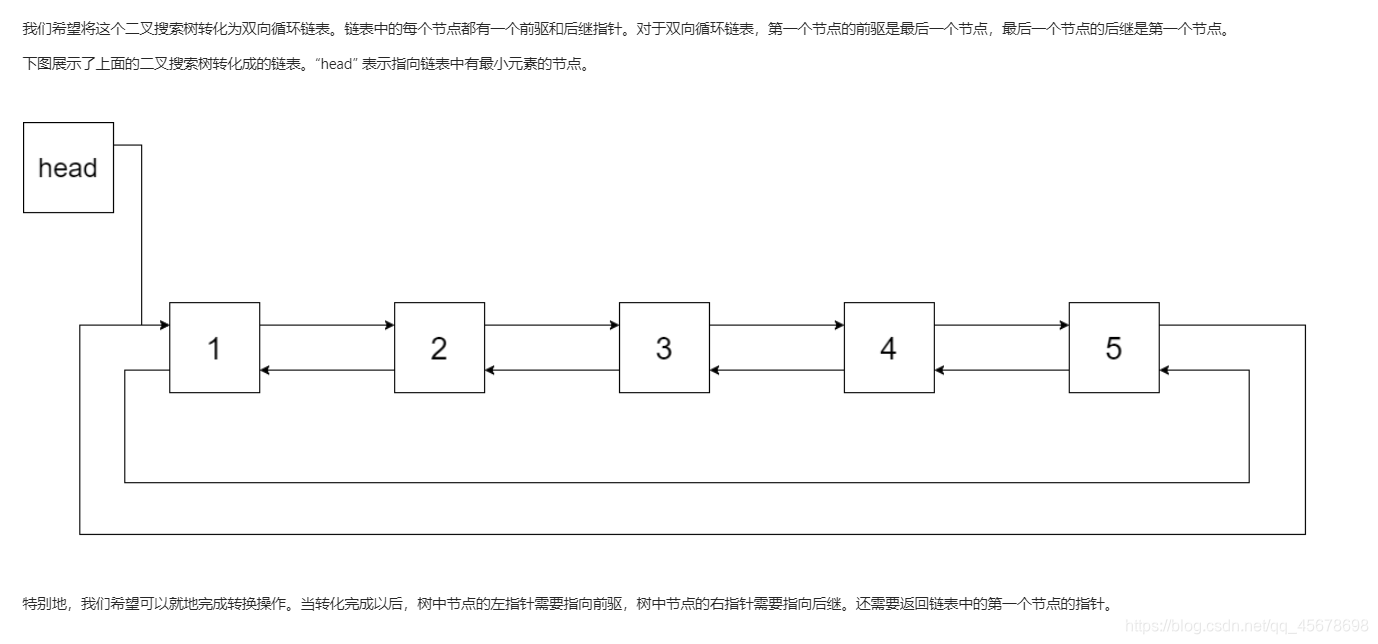
预备知识

1、二叉搜索树是我们的老朋友了，当他中序遍历的时候，恰好是一个单调递增的顺序，恰好满足本题要求。
2、循环双向链表的创建思路一：

3、循环双向链表的创建思路二：

利用方法一来完成链表构建

整体思路：

1、根据前序知识其中的构建方法一可知，我们必须知道前驱和后继，所以最好先把所有节点遍历出来，再进行连接，这样前驱后继很简单就知晓
2、首尾单独处理
3、一定考虑好特殊情况：一、空树。二、仅一个节点的树

具体代码（内附注释）

树定义：

class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};

class Solution {
public:
	vector< Node*> temp;//存节点的辅助vector
	Node* treeToDoublyList(Node* root) {
		if (root == nullptr) {
			return nullptr;
		}
		preorder(root);
		int num = temp.size();
		Node* head;//处理头节点
		head = temp.front();
		head->left = temp.back();
		if (num > 1) {
			head->right = temp[1];
		}
		else {
			head->right = head;//处理仅一个节点的树
		}
		for (int i = 1; i < temp.size() - 1; i++) {//中间的节点
			temp[i]->left = temp[i - 1];
			temp[i]->right = temp[i + 1];
		}
		if (num > 1) {//如果就一个节点，那么开头处理一次就够，节点数大于一，则处理尾巴节点
			temp[num - 1]->left = temp[num - 2];
			temp[num - 1]->right = head;
		}
		return head;
	}
	void preorder(Node* root) {//中根遍历求得递增序列
		if (root == nullptr) {
			return;
		}
		preorder(root->left);
		temp.push_back(root);
		preorder(root->right);
	}
};

（所有代码均已在力扣上运行无误）

经测试，该代码运行情况是(经过多次测试所得最短时间)：

利用方法二来完成链表构建

整体思路：

1、按照第二种方法，我仅仅知道前驱就行，最后处理首尾节点，所以完全就可以在中根遍历的时候，一边遍历，一边连线，但一定注意的是，要记录好开始的节点和前驱节点。
2、最开始没有head，程序无法开始拼出链表，自然无法标记pre ，只有找到最小的节点（即第一次从向左深入中走出来的时候），他就是head，此时pre为nullptr，这个时候开始标记，开视拼链表即可。

具体代码（内附注释）

注意：此种方法是从第二个节点开始拼链表，所以找到head,做好标记即刻退出，从第二个节点开始脸，首尾最后处理。

class Solution {
public:
	Node* treeToDoublyList(Node* root) {
		if (root == nullptr) {//程序健壮性
			return nullptr;
		}
		preorder(root);
		head->left = pre;//处理首尾
		pre->right = head;
		return head;
	}
private:
	Node *head = nullptr, *pre = nullptr;//pre是前驱节点，head是头节点
	void preorder(Node* cur) {
		if (cur == nullptr) {//出口
			return;
		}
		preorder(cur->left);
		if (pre == nullptr) {//找head，head没有程序不开始真正拼链表，找到第一个从不断向左走退出来的节点，那个就是最小的节点
		//此时没有pre 
			head = cur;
		}
		else {
			cur->left = pre;//看上方示意图
			pre->right = cur;
		}
		pre = cur;//该节点操作完之后，进入到下一个结点的时候，该节点就变成了前驱了，所以重新标记
		preorder(cur->right);
	}
};

（所有代码均已在力扣上运行无误）

经测试，该代码运行情况是(经过多次测试所得最短时间)：

时间复杂度 O(N)： N为二叉树的节点数，中序遍历需要访问所有节点。