淼淼刷力扣

引言

本人初次尝试写博客，希望各位看官大佬多多包容
有错误希望巨巨们提出来，我一定会及时改正，谢谢大家
在自己最好的年纪，找到了未来的目标
还有1年奋斗刷题，明年去面试实习，加油！
博主最近要参加竞赛，所以暂时调整训练计划。

题目一要求：

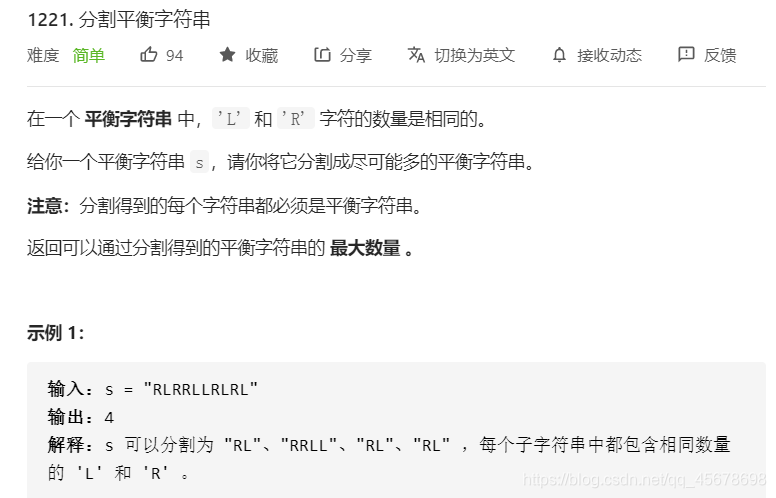
整体思路：

从前到后访问一次，看到L存入num_l,看到R存入num_r，然后一定看看这时候二者一不一致，因为题目要求尽可能多，所以要时时检查，一旦相等，则找到一个。

具体代码（内附注释）

class Solution {
public:
	int balancedStringSplit(string s) {
		int num_l = 0, num_r = 0;
		int answer = 0;
		for (int i = 0; i < s.size(); i++) {
			if (s[i] == 'L') {
				num_l++;
			}
			else {
				num_r++;
			}
			if (num_l == num_r) {
				answer++;
				num_l = 0;
				num_r = 0;
			}
		}
		return answer;
	}
};

（所有代码均已在力扣上运行无误）

经测试，该代码运行情况是(经过多次测试所得最短时间)：

时间复杂度：O(N)。

题目二要求

整体思路一：

很简单，就是简单的把B放进A，对A再次排序即可

具体代码一（快速排序）

快排思路：
1、定下两个哨兵，即两头(确定left 和 right)，确定参考点即左面开头的数值
2、左面参考点右面先动，反之左面先动。
3、快排本质就是让参考点左面都小于他，右面都大于他，所以右面出现小的，左面出现大的都属于异常，所以右面找比参考点小的，找到之后左面开始找比参考点大的，二者找到了，交换即可，一旦俩哨兵相遇了，说明参考点左面都小于他了，右面都大于他了。
4、最后把参考点从原来位置挪到这个正确位置就行

class Solution {
public:
	void merge(vector<int>& A, int m, vector<int>& B, int n) {
		for (int i = 0; i < n; i++) {
			A[m + i] = B[i];
		}
		QuickSort(A, 0, m + n - 1);
	}
	void QuickSort(vector<int>& A, int i, int j) {//快排
		if (i >= j) {
			return;
		}
		int item = A[i];//参考点
		int left = i;//俩哨兵
		int right = j;
		while (left != right) {//一直交换直到二者相遇
			while (right != left && A[right] > item) {//一定要记住，第一要务就是时时刻刻看着到没到结束位置呢
				right--;
			}
			while (right != left && A[left] <= item) {
				left++;
			}
			swap(A[left], A[right]);
		}
		swap(A[i], A[left]);
		QuickSort(A, i, left - 1);
		QuickSort(A, left + 1, j);
	}

	
};

（所有代码均已在力扣上运行无误）

经测试，该代码运行情况是(经过多次测试所得最短时间)：

具体代码二（堆排序）

堆排序方法：

1、在二叉堆的操作之中，最重要的是上浮和下沉，这里用下沉就足矣，且上浮下沉只是方向不同，书写方法类似。
2、排序的时候，第一我们手里的不是树，要先重整称为二叉堆(二叉堆是完全二叉树结构，用数组保存，父子之间有明确关系)，将手里面的变成树结构，第二：二叉堆最厉害的性质就是可以在O(1)在堆顶读出最大(小)元素，所以利用这个性质，每次都是把堆顶元素和最后一个元素交换，则未排序的部分就少了一（堆得规模少了一，已排序部分加了1），再次重整二叉堆就行了。（每次取走堆顶，把最后一个元素放到堆顶，规模减1，堆顶下沉完成重整)
3、下沉操作:本质上说即是，它因为自己"德不配位"，因为自己是个小节点，所以他看看他的后代有没有大于他的，把大的交上来，他自己下去的过程

注意：

完全二叉树因为涉及追溯父亲或者儿子，要经常乘除2操作，所以必须从1开始存储，要不然0*/啥没意义了！！！！！

class Solution {
public:
	void merge(vector<int>& A, int m, vector<int>& B, int n) {
		for (int i = 0; i < n; i++) {
			A[m + i] = B[i];
		}
		A.insert(A.begin(), 0);//调整存储，把0位置让出来，因为堆操作建立在存储起始位是1
		HeapSort(A);
		A.erase(A.begin(), A.begin() + 1);//排序后还原
	}
	
	void HeapSort(vector<int>& A) {//堆排序
		int num = A.size();//小技巧：大量调用size函数会降低速度
		for (int i = num - 1; i >= 1; i--) {//整堆，把A变成二叉堆
			A = down(A, i, num - 1);
			//这里大小范围解释：
			//因为我把零位置空出来了，所以说一切操作都要避免于0位置有交集
			//所以num会多一位，堆得规模为num-1
			//比如存入六个数，根据上面操作num=7，所以最后一个数
			//在A[num-1]处，所以i的范围有了
		}
		for (int i = num - 1; i > 1; i--) {
		//过程上述写过，不再赘述
		//i的起始处和上方说的一样
			swap(A[1], A[i]);
			A = down(A, 1, i - 1);//这里每次堆得规模少一，因为堆顶被拿走了
		}
	}
private:
//下沉函数形参：存储vector,何位置执行下沉，堆规模
	vector<int> down(vector<int>& A, int pos, int size) {//关键性的下沉操作
		int son = pos << 1;//先算，防止越界
		while (son <= size) {
			if (son + 1 <= size && A[son + 1] > A[son]) {
				son++;//找两个儿子中谁最大，并且一切操作之前先看看能否越界
			}
			if (A[son] <= A[pos]) {//出口，找到了<=自己的时候就结束了
				break;
			}
			swap(A[son], A[pos]);
			pos = son;
			son <<= 1;
		}
		return A;
	}
};

（所有代码均已在力扣上运行无误）

经测试，该代码运行情况是(经过多次测试所得最短时间)：

具体代码三（希尔排序）

总体思路：
1、希尔排序产生的原因是因为直接插入排序在面对大数量以及数据混乱的无力。
2、所以当数量大并且混乱的时候会出现效率降低，但我们还是想要用直接插入排序，所以我们可以把两个不利条件分而治之，分开分别处理，一次处理一个不利条件
3、我们分组，最开始每一组个数少但是乱，随着一组中的个数不断增多，但同时规整度也越来越高，分开之后效率就高了起来
4、分组就是不断除二，直到为1时为止，在每一组内直接插入排序。
5、直接插入时的技巧：

class Solution {
public:
	void merge(vector<int>& A, int m, vector<int>& B, int n) {
		for (int i = 0; i < n; i++) {
			A[m + i] = B[i];
		}
		shellSort(A);
	}
	//希尔排序，分组排序，开始组别大，随着排序次数增加，数组逐渐有序
	//希尔排序是对直接插入排序的一种优化，就是分组+插入,开始组间很大，排序个数少，数据乱，随着排序进行，个数逐渐增多，但是越来越规整，所以提高了速度
	void shellSort(vector<int>& A) {//拆分矛盾，不能既个数多有乱，所以拆开处理，要么乱个数少，要么规整个数多，再用插入排序，就不影响速度了
		int num_A = A.size();
		int num_sub = num_A >> 1;//既是组间距又是组数
		while (num_sub >= 1) {
			for (int i = num_sub; i < num_A; i++) {//这里是设计的最巧妙之处，找到第一个要处理的地方，后面都是要处理的
				//num_sub为多少那么就会有多少组，分组的时候都是从前往后分，所以从0到num_sub-1即是分的组数，从num_sub开始
				//为需要开始的序列
				int temp = A[i];
				int j = i;//i是不可移动的，所以做一个临时可动的变量j用于寻找最佳插入位置
				while (j - num_sub >= 0 && A[j - num_sub] > temp) {//这里判断的时候必须时j - num_sub，看他能不能向前走
					A[j] = A[j - num_sub];//向前找合适位置，把前面的数赋过去
					j -= num_sub;
				}
				A[j] = temp;//在合适位置把目标数据恢复
			}
			num_sub >>= 1;
		}
	}
};

（所有代码均已在力扣上运行无误）

经测试，该代码运行情况是(经过多次测试所得最短时间)：

具体代码四（归并排序）

整体思路：
1、就是先疯狂的分解，直到left>right(不合法退出)，或者left=right(仅一个节点)就可以停止了，之后再合并，左面先合并，右面再合并，最后整体合并，典型的回溯法，调用后根遍历模型即可。
2、这个方法本身性质就可以避免越界的情况。

class Solution {
public:
	void merge(vector<int>& A, int m, vector<int>& B, int n) {
		for (int i = 0; i < n; i++) {
			A[m + i] = B[i];
		}
		apart(A, 0, m + n - 1);
	}
	//归并排序，就是先分解再合并
	void apart(vector<int>& A, int i, int j) {//典型的回溯合并，向下分解
		if (i >= j) {//终止条件
			return;
		}
		int mid = (i + j) / 2;
		apart(A, i, mid);//后根
		apart(A, mid + 1, j);
		//写之后的融合代码的时候，可以找一个简单的样例写，再拿边界情况验证
		//辅助vector
		//走到这里的代表i-mid 和 mid+1-j 都已经整好了，剩下的就是把这个两个整体合并一下就行了，先存到辅助数组里，在复制即可
		//上下级传递的是指针
		vector<int> temp(j - i + 1, 0);
		int left = i;//left从i到mid，right从mid+1到j
		int right = mid + 1;
		int point = 0;
		while (left <= mid && right <= j) {
			if (A[left] <= A[right]) {
				temp[point++] = A[left++];//看谁小谁就下去放进辅助数组
			}
			else {
				temp[point++] = A[right++];
			}
		}
		while (left <= mid) {//把剩下的放进去
			temp[point++] = A[left++];
		}
		while (right <= j) {
			temp[point++] = A[right++];
		}
		left = i;
		point = 0;
		while (left <= j) {
			A[left++] = temp[point++];
		}
	}
	
};

（所有代码均已在力扣上运行无误）

经测试，该代码运行情况是(经过多次测试所得最短时间)：

具体代码五（利用c++ sort函数）

注：sort函数是最好的选择，开发c++的先辈大师们已经将sort函数开发的无比完美了，博主只是为了复习才写了前四种方法，毕竟我们要把算法学精，自己会写才是王道

class Solution {
public:
    void merge(vector<int>& A, int m, vector<int>& B, int n) {
        for (int i = 0; i != n; ++i) {
            A[m + i] = B[i];
        }
        sort(A.begin(), A.end());//这个函数是最好的选择
    }
};

时间复杂度：O((m+n)\log(m+n))。排序序列长度为 m+n，套用快速排序的时间复杂度即可，平均情况为 O((m+n)\log(m+n))。

整体思路二

利用已知：A和B都已经排好序，所以设立两个指针，初始时指向A和B的开头，每次让小的节点进入辅助vector直到其中一个为空，最后看谁有剩余就一股脑的全进来即可。

具体代码

博主主要练习了排序，这个没有写代码，下方的是官方题解代码

class Solution {
public:
    void merge(vector<int>& A, int m, vector<int>& B, int n) {
        int pa = 0, pb = 0;
        int sorted[m + n];
        int cur;
        while (pa < m || pb < n) {
            if (pa == m) {
                cur = B[pb++];
            } else if (pb == n) {
                cur = A[pa++];
            } else if (A[pa] < B[pb]) {
                cur = A[pa++];
            } else {
                cur = B[pb++];
            }
            sorted[pa + pb - 1] = cur;
        }
        for (int i = 0; i != m + n; ++i) {
            A[i] = sorted[i];
        }
    }
};

/*作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/sorted-merge-lcci/solution/mian-shi-ti-1001-he-bing-pai-xu-de-shu-zu-by-leetc/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。*/

时间复杂度：O(m+n)。指针移动单调递增，最多移动 m+n 次，因此时间复杂度为 O(m+n)。

整体思路三

利用已知：
1、A和B都已经排好序（递增）
2、A后面留有足够的空间容纳B，并且A后面是无意义的，可以随意覆盖，经证明，可知确实不会产生结果覆盖
综上，我们采用逆双指针方法，俩指针直接放在AB后面，谁大谁放进A的结尾，最后剩下谁就一股脑从后向前全放进A里
注：这样做可以节省大量空间

具体代码

代码转自官方题解

class Solution {
public:
    void merge(vector<int>& A, int m, vector<int>& B, int n) {
        int pa = m - 1, pb = n - 1;
        int tail = m + n - 1;
        int cur;
        while (pa >= 0 || pb >= 0) {
            if (pa == -1) {
                cur = B[pb--];
            } else if (pb == -1) {
                cur = A[pa--];
            } else if (A[pa] > B[pb]) {
                cur = A[pa--];
            } else {
                cur = B[pb--];
            }
            A[tail--] = cur;
        }
    }
};

/*作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/sorted-merge-lcci/solution/mian-shi-ti-1001-he-bing-pai-xu-de-shu-zu-by-leetc/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。*/

时间复杂度：O(m+n)。
指针移动单调递减，最多移动 m+n 次，因此时间复杂度为 O(m+n)。

空间复杂度：O(1)。
直接对数组 AA 原地修改，不需要额外空间。该算法亮点就是在此，相较于思路二节约了辅助空间。

综上

1、方法二从前到后，牺牲了空间
2、方法三从后到前，逆向做，利用了A后面开了足够大的空间足以放下B，节约了空间
3、方法二方法三使用时一定注意好他们分别的前提！！！！