数据结构3——二叉树

最新推荐文章于 2023-03-26 10:52:14 发布

原创最新推荐文章于 2023-03-26 10:52:14 发布 · 335 阅读

0 ·

CC 4.0 BY-SA版权

226.翻转二叉树

翻转一棵二叉树。

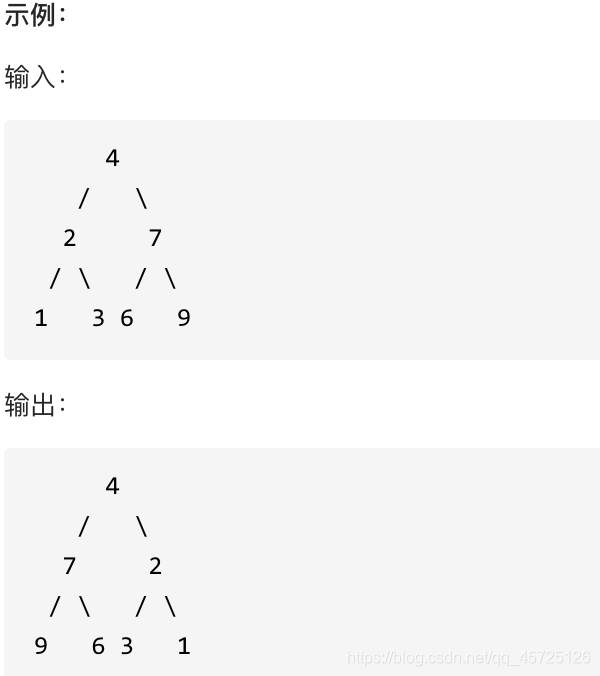
在这里插入图片描述
翻转二叉树其实很简单，我们每次只需要把当前结点的左右子树调换即可，通俗的说就是——左子树变右子树，右子树变左子树，那么我们如何实现呢？——两种方法：迭代和递归

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        #递归法
        if not root:return None
        #每次都将左右节点翻转
        root.left,root.right=root.right,root.left
        #然后对翻转后的左节点再进行翻转
        self.invertTree(root.left)
        self.invertTree(root.right)
        return root

        '''
        迭代法
        if not root:return None
        st=[]
        st.append(root)
        while st:
            node=st.pop()
            node.left,node.right=node.right,node.left
            if node.left:
                st.append(node.left)
            if node.right:
                st.append(node.right)
        return root
        '''

101.对称二叉树

给定一个二叉树，检查它是否是镜像对称的。

在这里插入图片描述
我们判断二叉树是否对称，其实也是比较两侧节点是否相等，但是注意我们此时比较的不是左右节点！——而是外侧和里侧节点

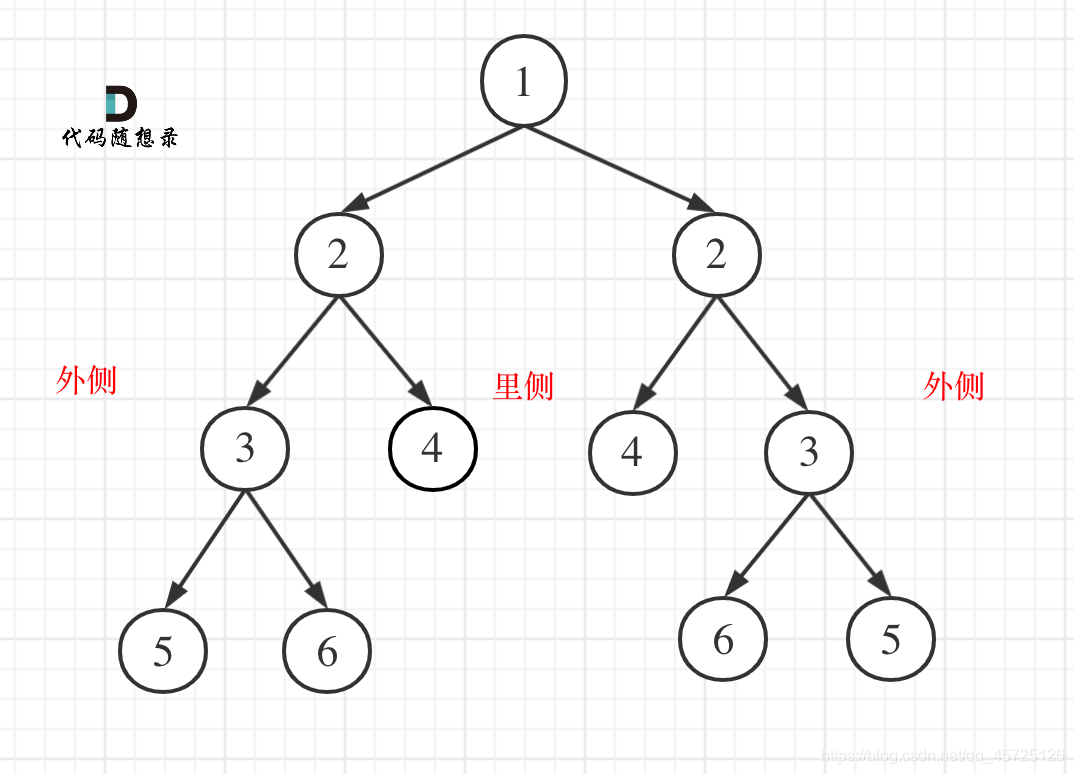
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:return True
        return self.theSame(root.left,root.right)
    def theSame(self,left:TreeNode,right:TreeNode):
        #我们首先判断这两个节点有空节点的情况
        if left and not right:return False
        elif not left and right:return False
        elif not left and not right:return True
        #然后当两个节点都不为空，判断它们的值是否相等
        elif left.val!=right.val:return False
        #此时经过上述的所有判断，递归到这一步代表此时两个节点都相等
        #可以将它们的子节点加入递归判断了
        outside=self.theSame(left.left,right.right)
        inside=self.theSame(left.right,right.left)
        #当外侧和里侧都相等，代表对称
        res=outside and inside
        return res

二叉树和N叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：给定二叉树 [3,9,20,null,null,15,7]，

在这里插入图片描述
返回最大深度3
这道题其实也是两种方法——递归与迭代，迭代就简单，和层序遍历一样，找到根节点那一层即可，递归就需要分别求出左右子树的深度，然后取两者中的最大值加1

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        #递归法
        Depth=self.getDepth(root)
        return Depth
    def getDepth(self,root):
        if not root:return 0
        #分别记录左右子树的深度
        left=self.getDepth(root.left)
        right=self.getDepth(root.right)
        #当递归完成之后，我们的结果取左右子树的最大深度加1（加上root）
        Depth=1+max(left,right)
        return Depth

        '''
        迭代法（其实就是层序遍历）
        if not root:return 0
        queue=collections.deque()
        res=0
        queue.append(root)
        while queue:
            size=len(queue)
            for _ in range(size):
                node=queue.popleft()
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            res+=1
        return res
        '''

N叉树
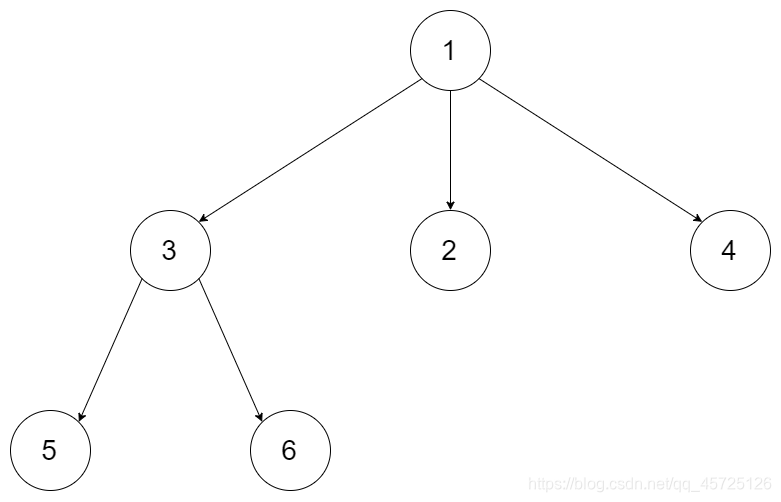
在这里插入图片描述
如图是一个三叉树，我们应该返回最大深度3，N叉树的特点就是用Node节点来存储，并且子树节点都是children（而不再用left，right区分）

"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""
import collections
class Solution:
    def maxDepth(self, root: 'Node') -> int:
        #迭代法,和二叉树的层序遍历有一点区别
        que=collections.deque()
        if root:
            que.append(root)
        depth=0
        while que:
        	#先记录每层的节点数，这也是这一层遍历的次数
            size=len(que)
            depth+=1
            for i in range(size):
                node=que.popleft()
                #对于每一个节点，都要将其所有的children节点加入队列
                for j in range(len(node.children)):
                    if node.children[j]:
                        que.append(node.children[j])
        return depth

    '''
    def maxDepth(self, root: 'Node') -> int:
    递归法
        return self.getDepth(root)
    def getDepth(self,root):
        if not root:return 0
        depth=0
        for i in range(len(root.children)):
            depth=max(depth,self.getDepth(root.children[i]))
        return depth+1
    '''

二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例:

给定二叉树 [3,9,20,null,null,15,7],
在这里插入图片描述
返回最小深度2
注意：很多做过二叉树最大深度的，都会遇到一个误区！举例说明

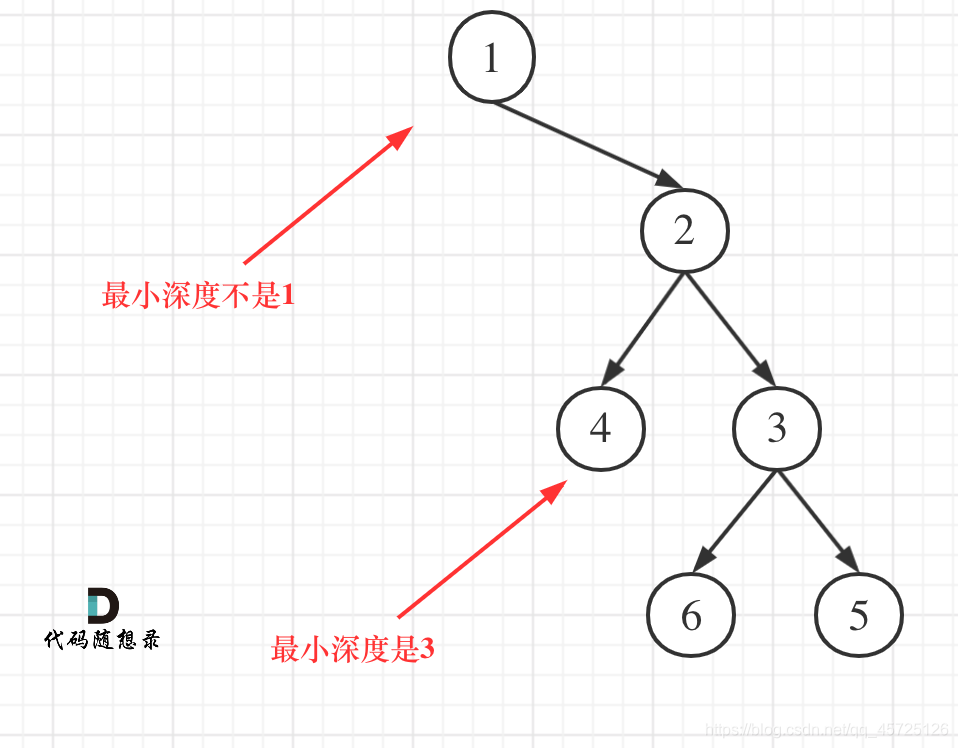
**我们找最小深度要找的时叶子节点！**如果像上述图片所示，我们还按照求最大深度的写法，分别求左右子树的最小深度加1的话，就会出错！

int leftDepth = getDepth(node.left);
int rightDepth = getDepth(node.right);
int result = 1 + min(leftDepth, rightDepth);
return result;//错误写法

正确的判断应该是，首先判断左右子树只有一个为空的情况,然后再判断两者都不为空或者同时为空，此时就是返回左右子树的最小深度加1

int leftDepth=getDepth(node.left)
int rightDepth=getDepth(node.right)
if not root.left and root.right:
	return 1+rightDepth
elif root.left and not root.right:
	return 1+leftDepth
return 1+min(leftDepth,rightDepth)

完整代码（迭代+递归）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
import collections
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        #递归法
        return self.getDepth(root)
    def getDepth(self,root):
        if not root:return 0
        left=self.getDepth(root.left)
        right=self.getDepth(root.right)
        #当左子树不为空但右子树为空时，最小深度应该是右子树深度加1
        if root.left and not root.right:
            return 1+left
        #右子树同理
        elif root.right and not root.left:
            return 1+right
        #当左右子树都不为空或者同时为空时，就取两者中的最小值即可
        return 1+min(left,right)
        '''
        迭代法
        if not root:return 0
        st=collections.deque()
        st.append(root)
        res=0
        while st:
            res+=1
            for _ in range(len(st)):
                node=st.popleft()
                #这里判断当前节点是否为叶子节点
                if not node.left and not node.right:
                    return res
                if  node.left:
                    st.append(node.left)
                if node.right:
                    st.append(node.right)
        return res
        '''

完全二叉树的节点个数

给你一棵完全二叉树的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例: 示例 1：输入：root = [1,2,3,4,5,6] 输出：6

示例 2：输入：root = [] 输出：0

示例 3：输入：root = [1] 输出：1

提示：

树中节点的数目范围是[0, 5 * 10^4]
0 <= Node.val <= 5 * 10^4
题目数据保证输入的树是完全二叉树
思路
其实这道题就是要遍历二叉树，每遍历一个节点就给节点数加1即可，那么遍历整颗二叉树也可以用迭代法和递归法来解决

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def countNodes(self, root: TreeNode) -> int:
        #迭代法
        if not root:return 0
        st=[root]
        res=0
        while st:
            for _ in range(len(st)):
                node=st.pop()
                res+=1
                if node.right:
                    st.append(node.right)
                if node.left:
                    st.append(node.left)
        return res
        '''
        递归法
        if not root:return 0
        res=0
        if root:res+=1
        left=self.countNodes(root.left)
        right=self.countNodes(root.right)
        return left+right+1
        '''

判断二叉树是否平衡

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]——返回True

在这里插入图片描述
示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]——返回False

在这里插入图片描述
以上两个例子说明，我们不仅要分别判断左右子树是否平衡，最后还要将左子树和右子树放在一起判断最大高度差
思路
如何判断当前传入节点为根节点的二叉树是否是平衡二叉树呢，当然是左子树高度和右子树高度相差。

分别求出左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则则返回-1，表示已经不是二叉树了。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        res=self.getDepth(root)
        return True if res!=-1 else False
    def getDepth(self,root):
        if not root:return 0
        leftDepth=self.getDepth(root.left)
        if leftDepth==-1:return -1
        rightDepth=self.getDepth(root.right)
        if rightDepth==-1:return -1

        res=0
        if abs(rightDepth-leftDepth)>1:
            res=-1
        else:
            res=max(leftDepth,rightDepth)+1
        return res