2021-6-8 力扣每日一题

问题描述：

​ 有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

• 如果 x == y，那么两块石头都会被完全粉碎；
• 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

示例1：

输入：stones = [2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

示例2：

输入：stones = [31,26,33,21,40]
输出：5

示例3：

输入：stones = [1,2]
输出：1

思路：

​ 因为最近动归的题有点儿多，所以这里我想先聊一聊关于动归的一些简单看法。在算法导论里讲到，分治和动归的思想是类似的，二者都是通过解决子问题，将子问题组合起来，进而求出原问题的解。不同在于，分治是分为多个互不相交的子问题，而在动态规划中，原问题的不同子问题，可能存在相同的子子问题。如果在解决这样问题的时候，使用分治的过程，那么我们将存在很多重复计算的过程，所以我们更热衷于将子问题的解先保存下来，在下次需要的时候就可以直接使用，避免了不必要的计算工作。

​ 在动态规划中有一个很经典的背包问题，背包问题有很多种，但都是从0-1背包发展而来，解决这个深入理解0-1背包问题对理解动态规划有很大的帮助。这里谈一谈我们0-1背包问题的简单理解。

---

​ 问题大概就是给一定数量的物品，每个物品有自己的价值和重量，让你在重量和不超过某个值的情况下，选出价值最大的那个组合。

​ 刚接触这个问题的时候，想到的是贪心，因为如果一件物品价值又高，重量又轻，那么选它一定是最值的呀，所以就按照价值/重量做一个排序，在重量不超过限定值的情况下选前面的即可。乍一想没啥问题，但是一推敲就会发现问题，因为这样我们无法保证选完之后重量刚好达到我们限定的重量。这样就会出现一个问题，到最后我还剩5个单位的重量，这里只剩下两个物品，一个是价值2重量1，一个是价值3，重量5，显然根据性价比来看，选第一个是好的，但是结果却是选第二个更好。也就是说在这个问题里并不是性价比越高就越应该选。那么我们怎么制定策略呢？如果不按照性价比来看，那按照什么来看。

​ 结果是不管是按照价值，重量，性价比来作为贪心的准则，都无法得到正确的结果，因为这个问题本身并不是一个限定条件，而是两个，价值和重量，而这两个的比值也无法表示这个标准。我们好像陷入了盲区

---

【动态规划】

物理学中有一个习惯，当一个系统在表示世界的时候出现了误差，我们就需要对系统进行修正或者重新建立一个系统，从牛顿的经典力学理论到爱因斯坦的相对论即使如此。这里同样如此，为了解决这个问题，我们亟需新的思想，新的理论，而这个思想就是动态规划。

​ 不敢标榜自己对动态规划理解的有多么透彻，在这里也只是发表一下自己的拙见。

​ 我们之前贪心的思路是从某一个标准出发，如果这个物品更贴合这个标准，那么选它就是好的，如果离这个标准越远，那么就越不应该选它。但事实证明这样是错的。那或许我们可以从问题的本身出发。因为我们总能找到一个方案，使得这个结果最大，这里抛开传统的观点，可能这个方案中有那个性价比最低的物品，等等等等。但总是存在一个方案是所有方案中结果最大的那个。

​ 有了上面的那个思维，我们就需要找到那个方案就行了呀。再进行抽象一下，方案与方案的不同根本在于什么？在于某一个物品有没有被选，如果某个方案是选了1号，2号，3号。另一个方案同样选了1号，2号，3号。那么这两个方案就是相同的。同理，有一个不同的话，这两个方案就是不同的。例如某个方案选了1，2，3号，另一个方案选了1,2,4号，那么这两个方案就是不同的方案。那么这和我们最后的结果有什么关系呢？暴力一点儿说，我们可以枚举所有的方案数，一共有2的n次方种方案数，n表示待选的个数，我们在这些方案中找到满足重量小于标准值并且结果最大的那个就行了。

​ 但这样也太慢了吧，不过总算是找到了一条解决的道路，因为我们上一个思路是没办法求解的。有了方向，我们就可以对其进行优化了。

​ 这里我们思考一下这种方案为什么这么慢，因为它枚举了所有的方案数，将每一种方案都算一下，所以它慢，但这样是有必要的吗？答案肯定是没必要的。因为我们有限制条件啊，如果在某个计算的过程中，发现违反了这个限制条件，我们就没有必要再算下去了，比如说某个方案连续选了前五个物品，重量已经超了，那我们就没必要再去枚举后面的情况，因为后面的也一定选不上。

​ 虽然话是这么说，那我们如何在代码中去实现这个筛选的过程呢？还记得上面加粗的字吗，我们区别方案的不同，在于某一个物品有没有被选，在程序里要怎么表示有没有被选呢？

• 我们可以定义一个数组dp [ i ] [ j ] 表示在前 i 个物品中，选择总重量不超过 j 的物品的最大价值。
• 接着遍历每一个物品
  • 如果这个物品的重量比 j 要大，那肯定是不能选它的呀，因为它本身就已经超了最大的重量，这时dp[ i ] [ j ] = dp[ i-1 ] [ j ]
  • 而如果这个物品的重量没有j大，那我们就可以选它了，但是具体选不选呢？
    • 如果选了的话，总重量还是不能超过 j 啊，那么我们就应该得到dp[ i - 1] [ j - weight [ i ] ] 的值再加上value[ i ]。
    • 如果没选的话，那价值还是dp[ i-1 ] [ j ]，比较这两个谁大即可，来决定到底选不选。
• 等我们遍历完数组，最后的结果就是，所有的物品中，重量不超过总重量的最大价值，这样我们就得到了问题的解

---

​ 这里我们可以看到，动归其实也使用到了分治的思想，我们要求的是一个大目标，那我们就先求一个一个小目标，接着根据小目标推导出大目标。不得不说，挺巧妙的。

---

​ 言归正传，这个问题应该怎么写呢？依然是动归，和0-1背包类似，我们可以将石头分为两组，一个就是选，一个就是不选，或者说一个是前面是+，另一个前面是 - 。最终的结果总能使用他们的和来表示，但并不是每一个结果都是合法的，我们只需要求解出其最小的非负整数即可。

​ 当为 + 的和为 - 的和接近总和的一半的时候，我们就得到了最优的结果，这里我们定义 dp[ i+1 ] [ j ]表示前 i 个石头能否凑出 j 来，根据0-1背包的思路，考虑到第i个石头

因此，转移方程为：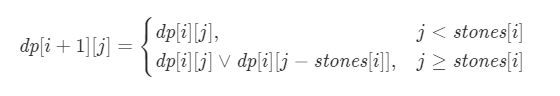

其中V是逻辑或运算，这样我们就可以求解出最后的结果。

Java代码：

/**
* @Description: 力扣1049题题解
* @return: 返回结果
* @Author: Mr.Gao
* @Date: 2021/6/8
*/
public int lastStoneWeightII(int[] stones) {
    int n = stones.length;
    int sum = 0;
    for (int stone : stones) {
        sum+=stone;
    }
    int mid = sum/2;
    boolean[][] dp = new boolean[n+1][mid+1];
    dp[0][0] = true;
    for(int i=0;i<n;i++){
        for(int j=0;j<=mid;j++){
            if(j<stones[i]){
                dp[i+1][j] = dp[i][j];
            }else{
                dp[i+1][j] = dp[i][j]||dp[i][j-stones[i]];
            }
        }
    }
    for(int j = mid;;j--){
        if(dp[n][j]){
            return sum-2*j;
        }
    }
}

• 两天的高考，两天的背包，不禁让人回想起当年的自己。不说遗憾，只说无悔…
• 码字不易，后半段解释的不太好，还望动动小手点个赞