算法实验报告（第k小的数+重数+棋盘覆盖问题）

---

目录

---

快速排序及第k小数

思路

快速排序的性质：当一次排序完成后，左边元素一定比基准元素小，右边元素一定比基准元素大。因此选择第k个元素作为基准，设置左右两个哨兵，当哨兵相遇的时候证明这一趟排序已经完成，此时虽然基准左右是无序的，但是和基准元素的大小关系是已知的。
设定左指针left和右指针right，每次左侧元素交换都会使基准数变小，和右侧元素交换都会使基准数变大。
一个注意点是，与右侧元素交换之后，可能前一次与左侧元素交换结果需要调整，因此需要在每一次循环中只进行一次左侧/右侧的元素交换，防止出现丢失前一次交换结果的情况。
也可以理解成先判断是否符合条件，然后移动哨兵。

代码

package Algorithms_算法.实验;

import java.util.Arrays;

public class quickSort {
    public int quick_sort(int[] nums,int k){
        int left = 0,right = nums.length-1;
        int tmp = nums[k-1];
        int tmp1 = 0;
        while(left < right){
            left = 0;
            right = nums.length-1;
            while(nums[left] < nums[k-1]) {
                ++left;
            }
            tmp1 = nums[left];
            nums[left] = nums[k-1];
            nums[k-1]=tmp1;
            System.out.println(Arrays.toString(nums));

            while(nums[right] > nums[k-1]) {
                --right;
            }
            tmp1 = nums[right];
            nums[right] = nums[k-1];
            nums[k-1]=tmp1;
            System.out.println(Arrays.toString(nums));
            System.out.println();
        }
        return nums[k-1];
    }

    public static void main(String[] args) {
        int[] nums = {9,7,5,3,1,8,6,4,2};
        int ans = new quickSort().quick_sort(nums,6);
        System.out.println(ans);
    }
}

运行结果

1到9的乱序排列输出第6小的元素，例如第一次和右侧元素交换时，左侧的8和新的基准元素2仍需要一次交换，这就需要回到原来的左侧哨兵的位置。

重数

题目

给定含有N个元素的多重集合S，每个元素在S中出现的次数称为该元素的重数，多重集合S中重数最大的元素称为多重集合S的众数，众数的重数称为多重集合S的重数，试求一个给定多重结合的重数和众数；
例如：S={a,b,b,b,f,f,4,5}的重数是3，众数是b

思路

利用hashmap结构:<字符，字符出现的次数>为entry数对存入hashmap，每次遇到不同的元素就新建entry，遇到相同的元素就更新值。最后遍历，得到出现最多的字符和他对应的次数。

代码

package Algorithms_算法.实验;

import java.util.HashMap;
import java.util.Map;

public class MostFrequentNumber {
    public Map.Entry<String,Integer> solve(String[] elements){
        HashMap<String,Integer> myMap = new HashMap<>();
        for(int i=0;i<elements.length;i++){
            if(myMap.containsKey(elements[i])){
                int frequency = myMap.get(elements[i]) + 1;
                myMap.put(elements[i],frequency);
            }else{
                myMap.put(elements[i],1);
            }
        }
        Map.Entry<String,Integer> ans = null;
        int maxFrequency = 0;
        for(Map.Entry<String,Integer> tmp : myMap.entrySet()){
            if(tmp.getValue() > maxFrequency){
                ans = tmp;
            }
        }
        return ans;
    }

    public static void main(String[] args) {
        String[] elements = {"a","a","c","1","2","3","3","3","3","3","3","3"};
        Map.Entry<String,Integer> ans = new MostFrequentNumber().solve(elements);
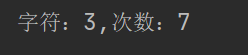
        System.out.println("字符："+ans.getKey()+",次数："+ans.getValue());
    }
}

运行结果

---

棋盘覆盖问题

题目

在一个2k×2k 个方格组成的棋盘中，恰有一个方格与其它方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。

思路

可以把特殊方格看成是黑色的，其余部分是白色的，题目就是要我们用黑色方块覆盖棋盘。运用分治法思想，当满足条件：棋盘大小等于2^k的时候，可以每次把棋盘分成四个大小相同的子棋盘，特殊方格只可能存在与一个子方格中。对于没有特殊方格的三个子方格，在他们相邻的中心点处，用一个L型骨牌去覆盖，这样就满足四个方格都有特殊方块，可以递归求解了。

ChessBoard(int tr,int tc,int dr,int dc,int size)

上式是递归函数，前两个参数是左上角坐标，中间两个参数是特殊方格的坐标，最后一个是方格大小，也是控制递归回溯的条件。每次求解子问题只有两种情况：
1.特殊方格在这个子方格中，那么子问题的特殊方格坐标就是原问题的特殊方格坐标。
2.特殊方格在不这个子方格中，那么可以通过用一个L型骨牌来覆盖三个没有特殊方格的区域，此时子方格的新特殊方格位置是可以求解的，更新特殊方格位置。
然后进行子问题求解。

代码

package Algorithms_算法.实验;
/**
 * tr : 棋盘左上角的行号，tc棋盘左上角的列号
 * dr : 特殊方格左上角的行号，dc特殊方格左上角的列号
 * size ：size = 2^k 棋盘规格为2^k*2^k
 */
public class ChessBoardCoverage {
    int tile = 1;//全局变量 骨牌编号
    int [][] Board;//棋盘

    public ChessBoardCoverage() {
        Board = new int[8][8];
    }
    public void ChessBoard(int tr,int tc,int dr,int dc,int size){
        if(size == 1) {
            return;
        }
        int t = tile++;//L型骨牌编号
        int halfSize = size/2;//分割棋盘
        //覆盖左上角子棋盘
        if(dr < tr+halfSize && dc < tc+halfSize){//特殊方格在左上子方格中
            ChessBoard(tr,tc,dr,dc,halfSize);
            //可以缩小范围，注意定点和特殊方格位置不变，因为缩小的都是没有方格的部分
        }
        else{//特殊方格不在左上子方格中，无论在三个中的哪里，都可以用一种骨牌包围这个特殊方格，
            // 这样左上子方格的右下角就是特殊方格了
            Board[tr+halfSize-1][tc+halfSize-1] = t;
            //更新特殊方格位置这个时候又满足第一种情况：特殊方格在左上子方格中，递归
            ChessBoard(tr,tc,tr+halfSize-1,tc+halfSize-1,halfSize);
        }
        //右上角子棋盘，注意边界条件
        if(dr < tr + halfSize && dc >= tc + halfSize){
            ChessBoard(tr,tc+halfSize,dr,dc,halfSize);
        }
        else{//队于右上角方格，第 halfSize - 1行，第 0 列，加上基址即可
            Board[tr + halfSize - 1][tc + halfSize] = t;
            ChessBoard(tr,tc+halfSize,tr+halfSize-1,tc+halfSize,halfSize);
        }

        if(dr >= tr+halfSize && dc < tc+halfSize){
            ChessBoard(tr + halfSize,tc,dr,dc,halfSize);
        }
        else {
            Board[tr + halfSize][tc + halfSize - 1] = t;
            ChessBoard(tr + halfSize,tc,tr + halfSize,tc + halfSize-1,halfSize);
        }

        if(dr >= tr+halfSize && dc >= tc+halfSize) {
            ChessBoard(tr + halfSize,tc + halfSize,dr,dc,halfSize);
        }
        else {
            Board[tr + halfSize][tc + halfSize] = t;
            ChessBoard(tr + halfSize,tc + halfSize,tr + halfSize,tc + halfSize,halfSize);
        }
    }
    public static void main(String[] args) {
        ChessBoardCoverage demo = new ChessBoardCoverage();
        demo.ChessBoard(0,0,2,3,8);
        for(int i=0; i<8; i++){
            for(int j=0; j<8; j++){
                System.out.print(String.format("%3d",demo.Board[i][j]));
            }
            System.out.println();
        }
    }
}

运行结果