算法实验报告2——贪心
目录
一、背包问题
题目
有一个背包,背包容量是M=150。有7个物品,物品可以分割成任意大小。
要求尽可能让装入背包中的物品总价值最大,但不能超过总容量。
物品 A B C D E F G
重量 35 30 60 50 40 10 25
价值 10 40 30 50 35 40 30
思路
把所有物品的平均价值求出来,按从大到小排列,贪心的选择最大的那个物品,直到剩余空间不足以选择整个物品时,选择这个物品的一部分,所求即是结果。
细节
排序的时候为了能够让平均价值排序之后仍然和原来的价值对应,使用了二维数组,以平均价值为排序基准,C++可以使用pair或结构体实现。这里有待优化。
代码
算法部分
public double solve(int[] weights,int[] values,int size) {
double[][] per_value = new double[weights.length][3];
double sum = 0;
for(int i=0;i< per_value.length;i++){
per_value[i][0] = values[i];
per_value[i][1] = weights[i];
per_value[i][2] = (values[i]+0.0) / weights[i];
}
System.out.println(Arrays.deepToString(per_value));
Arrays.sort(per_value, new Comparator<double[]>() {
@Override
public int compare(double[] o1, double[] o2) {
return o1[2] < o2[2] ? -1:1;
}
});
System.out.println(Arrays.deepToString(per_value));
int flag = per_value.length-1;
while(size > 0){
if(size >= per_value[flag][1]){
size-=per_value[flag][1];
sum+=per_value[flag][0];
System.out.println(size+","+sum);
flag--;
}else{
double loader = (size+0.0) / per_value[flag][1];
sum+=per_value[flag][0]*loader;
break;
}
}
return sum;
}
输入输出处理
public static void main(String[] args) throws IOException{
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
System.out.println("输入背包大小");
int size = Integer.parseInt(reader.readLine());
System.out.println("输入物品数量");
int n = Integer.parseInt(reader.readLine());
int[] weights = new int[n];
int[] values = new int[n];
System.out.println("输入背包物品重量");
String strweight = reader.readLine();
String[] strweights = strweight.split(" ");
System.out.println(Arrays.toString(strweights));
for(int i=0;i<n;i++){
weights[i] = Integer.parseInt(strweights[i]);
}
System.out.println("输入背包物品价值");
String strvalue = reader.readLine();
String[] strvalues = strvalue.split(" ");
for(int i=0;i<n;i++){
values[i] = Integer.parseInt(strvalues[i]);
}
Package demo = new Package();
double ans = demo.solve(weights,values,size);
//double ans = demo.solve(new int[]{35,30,60,50,40,10,25},new int[]{10,40,30,50,35,40,30},150);
System.out.println("价值"+ans);
}
运行结果

、
二、照亮的山景
题目
在一片山的上空,高度为T处有N个处于不同位置的灯泡,如图。如果山的边界上某一点于某灯i的连线不经过山的其它点,我们称灯i可以照亮该点。开尽量少的灯,使得整个山景都被照亮。山被表示成有m个转折点的折线。
提示:照亮整个山景相当于照亮每一个转折点。

思路
一座山想要能被照亮,那么把这座山的两侧分别延长,与灯所在的高度相交于两个点,在这个区间内如果有一盏灯,就可以照亮这座山,如果没有,就必须在区间两侧各有一盏灯。那么我们把每座山的区间放到一个集合中,遍历所有的灯,每次贪心的寻找覆盖区间最多的灯,同时将已经照亮的山移出集合,标记灯为已使用,直到集合为空,所求的灯的数量就是最小的灯的数量。
细节
用二维数组代替集合,节约数据结构带来的开销。
for(int i=2;i<x.length;i+=2){//每座山峰山顶之间隔一个点
x1 = x[i-2];
x2=x[i-1];
x3=x[i];
y1 = y[i-2];
y2=y[i-1];
y3=y[i];
//double k1 = (y2-y1)/(x2-x1+0.0),k2=(y3-y2)/(x3-x2+0.0);
//(x,height),
//(height-y2)/(xi-x2)=ki
sections[i-2][0] = (height*(x2-x1) +x1*y2 -x2*y1)/(y2-y1);
sections[i-2][1] = (height*(x2-x3) +x3*y2 -x2*y3)/(y2-y3);
}
利用斜率的计算公式,求出每座山的区间。
int max = 0,index = 0;
int count = sections.length;
ArrayList<Integer> ans = new ArrayList<>();
max表示最大的覆盖区间个数,count用来计算还有几座山没被照亮,初值为山的数量。
ans用来记录这盏灯覆盖的区间。
lights[i] > sections[j][1] && lights[i] < sections[j][0]
判断灯的条件
代码
public void solve(int[] x,int[] y,int height,int[] lights){
int[][] sections = new int[x.length-2][2];
int x1,x2,x3,y1,y2,y3;
//只要构成山峰,数组一定是奇数
for(int i=2;i<x.length;i+=2){//每座山峰山顶之间隔一个点
x1 = x[i-2];
x2=x[i-1];
x3=x[i];
y1 = y[i-2];
y2=y[i-1];
y3=y[i];
//double k1 = (y2-y1)/(x2-x1+0.0),k2=(y3-y2)/(x3-x2+0.0);
//(x,height),
//(height-y2)/(xi-x2)=ki
sections[i-2][0] = (height*(x2-x1) +x1*y2 -x2*y1)/(y2-y1);
sections[i-2][1] = (height*(x2-x3) +x3*y2 -x2*y3)/(y2-y3);
}
int max = 0,index = 0;
int count = sections.length;
ArrayList<Integer> ans = new ArrayList<>();
while(count > 0){
ArrayList<Integer> tmp = new ArrayList();//存选出的灯所关联的区间
for(int i=0;i<lights.length;i++){
ArrayList<Integer> related = new ArrayList();//存储当前灯关联的区间
//int num = 0;
for(int j=0;j< sections.length;j++){
if(lights[i] > sections[j][1] && lights[i] < sections[j][0]){
//num++;
related.add(j);
}
}
int num = related.size();
if(num > max){
max = num;
index = i;
tmp = related;
}
}
//此时index是覆盖区间最多的灯的下标
count-=tmp.size();
System.out.println(lights[index]);
Iterator itr = tmp.iterator();
while(itr.hasNext()){
Integer t = (Integer) itr.next();
sections[t][0] = sections[t][1] = -1;
}
}
}
三、搬桌子问题
题目
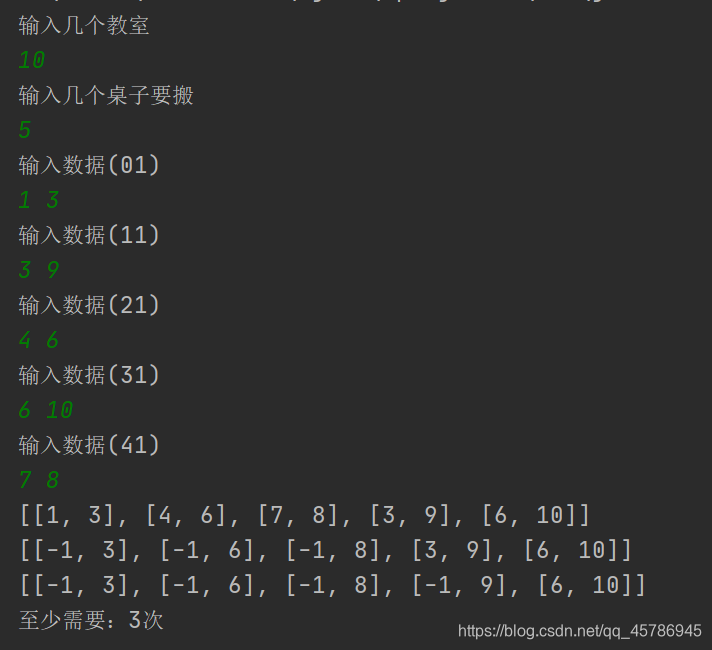
某教学大楼一层有n个教室,从左到右依次编号为1、2、…、n。现在要把一些课桌从某些教室搬到另外一些教室,每张桌子都是从编号较小的教室搬到编号较大的教室,每一趟,都是从左到右走,搬完一张课桌后,可以继续从当前位置或往右走搬另一张桌子。输入数据:先输入n、m,然后紧接着m行输入这m张要搬课桌的起始教室和目标教室。输出数据:最少需要跑几趟。
思路
按目的地升序排序,每次选择目的地最近的任务完成,类比于结束时间最早的任务。完成之后把该任务移出任务集,再次遍历,遍历次数即为趟数。
细节
Arrays.sort(works, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[1] < o2[1] ? -1 : 1;
}
});
根据目的地升序排列。
每次执行都先寻找第一个待执行的任务,然后寻找待执行任务被执行之后的下一个可执行任务,起点前移,直到无法选择,认为这一趟已经结束了。
代码
算法部分
public int solve(int m,int n,int[][] works){
int ans = 0;
Arrays.sort(works, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[1] < o2[1] ? -1 : 1;
}
});
// System.out.println(Arrays.deepToString(works));
//按目的地升序排序
int start = 0,end = 0;//这一趟开始的任务和结束的任务编号
//int startTime=0,endTime=0;
int count = m,perMov=0;//循环条件count,每次完成的任务次数perMov
while(count > 0){
System.out.println(Arrays.deepToString(works));
start = end = 0;//重新找
perMov = 0;
while(start < m){
while(start <m && works[start][0] <= 0){
start++;
}
//找到第一个没有执行的任务
works[start][0]=-1;
//执行过的任务开始时间为-1
while (end < m && works[end][0] < works[start][1]){
end++;
}
//找到第一个可以接在后面执行的任务,更新位置
start = end;
perMov++;
}
count-=perMov;
ans++;
}
return ans;
}
输入输出处理
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
System.out.println("输入几个教室");
int n = Integer.parseInt(reader.readLine());
System.out.println("输入几个桌子要搬");
int m = Integer.parseInt(reader.readLine());
int[][] works= new int[m][2];
for(int i=0;i<m;i++){
System.out.println("输入数据("+i+1+")");
String str = reader.readLine();
String[] ss = str.split(" ");
// System.out.println(Arrays.toString(ss));
works[i][0] = Integer.parseInt(ss[0]);
works[i][1] = Integer.parseInt(ss[1]);
}
move_chairs demo = new move_chairs();
System.out.println("至少需要:"+demo.solve(m,n,works)+"次");
}
运行结果
四、八皇后问题
题目
8皇后问题是一个广为人知的问题:将8个皇后放在8×8的棋盘上,皇后之间不能互相攻击,求各种放法。更一般的,把8换成n,其解法个数是随n成几何级增长的,因此程序运行时间也是几何级别的。现在我们关注这样一个问题,既然不能很快的把所有解都枚举出来,那么我们能不能很快的求出一个解来呢?
思路
1.规则:西洋棋的皇后可以吃掉直线上的任何棋子,包括直线和对角线。
2.如何减少递归次数:
如果这一列检查过,这一列其他个字就不用检查了,所以可以用某一行的每一个元素来代表这一整列;
主对角线上元素的j - i是一个常数,副对角线上元素的的j + i是一个常数,所以可以用一个元素来代表整条对角线;
这样,原来需要检查行,列,两条对角线的问题就被化简成只要检查三个元素的问题。
行:元素是一行一行放置的,不需要检查,但是数组下标最好从1开始。
列:只需要检查每一列的任意一个元素就可以
主对角线:只需要检查 primary_line【j-i】
副对角线:只需要检查sub_line【i+j】
这样,原本需要像老鼠走迷宫一样一步步试,不符合再回退的情况就化简成了一次性检查的问题。
细节
columns = new int[9];//同一列是否有
primary_line = new int[2*8+1];//左上到右下的主对角线
sub_line = new int[2*8+1];//副对角线
行+列 / 行+8-列 是定值,因此可以用一维数组来代替二维数组检测把皇后的重复问题。为了方便,数组下表从1开始记作皇后的标号。为了不越界,所以需要记录数组足够大。本题是8皇后,横纵坐标之和最大不过是8+8,因为下标0舍弃,所以用8+8+1。
Arrays.fill(columns,1);
Arrays.fill(primary_line,1);
Arrays.fill(sub_line,1);
初始值为1表示有一个资源,0表示资源已被占用,类比操作系统的临界资源。
if(columns[j] == 1 && sub_line[i+j] == 1 && primary_line[i+8-j] == 1){
queen[i] = j;
columns[j] = 0;
primary_line[i+j] = 0;
sub_line[i+8-j] = 0;
backtrack(i+1);
//所有的递归过程共享全局变量,所以递归的时候虽然没有带参数,但是已经把上一次的结果带进去了
//无论这一次递归结果,消除这一次的选择,回溯
columns[j] = 1;
primary_line[i+j] = 1;
sub_line[i+8-j] = 1;
每个皇后需要一个列资源,一个主对角线资源,一个副对角线资源,如果都有的话就分配给他,同时继续递归。通过全局变量来控制每次递归保留前一次的结果,如果不能递归,就判断
如果已经摆好了,就打印结果,同时回退。
否则直接回退。
回退的同时释放之前占用的资源。
for(int j=1;j<=8;j++)
遍历寻找哪个位置可以放皇后,而不是第几个皇后,第几个显示在递归层数里。
代码
private int[] columns;
private int[] primary_line;
private int[] sub_line;
private int[] queen;
public 八皇后(){
columns = new int[9];//同一列是否有
primary_line = new int[2*8+1];//左上到右下的主对角线
sub_line = new int[2*8+1];//副对角线
// 行+列 / 行+ 8-列 是定值,但是不能越界,所以需要记录数组足够大,
// 最大不过是8+8,因为下标从0开始,所以用8+8+1
queen = new int[9];//统一采用从下标1开始
Arrays.fill(columns,1);
Arrays.fill(primary_line,1);
Arrays.fill(sub_line,1);
}//1表示有一个资源,0表示资源已被占用
public void backtrack(int i){
if(i > 8){
showAnswer();
}else{
//我一开始想错了,以为这是第j个皇后的位置,其实这是遍历数组寻找可能放置第i个皇后的位置
for(int j=1;j<=8;j++){
if(columns[j] == 1 && sub_line[i+j] == 1 && primary_line[i+8-j] == 1){
queen[i] = j;
columns[j] = 0;
sub_line[i+j] = 0;
primary_line[i+8-j] = 0;
backtrack(i+1);
//所有的递归过程共享全局变量,所以递归的时候虽然没有带参数,但是已经把上一次的结果带进去了
//无论这一次递归结果,消除这一次的选择,回溯
columns[j] = 1;
sub_line[i+j] = 1;
primary_line[i+8-j] = 1;
}
}
}
}
int num = 0;
public void showAnswer(){
num++;
System.out.println("/n解答"+num);
for(int y=1;y<=8;y++){
for(int x=1;x<=8;x++){
if(queen[y] == x){
System.out.print("Q");
}else{
System.out.print(".");
}
}
System.out.println();
}
}
运行结果(部分)

五、素数测试
题目
Miller-Rabin测试的实现
思路
1.求出(a*b)%n
2.求出(a^b)%n
3.运用定理
费马小定理:对于素数p和任意整数a,有a^p ≡ a (mod p)(同余)。
反过来,满足a^p ≡ a(mod p),p也几乎一定是素数。
伪素数:如果n是一个正整数,如果存在和n互素的正整数a满足 a^(n-1) ≡ 1(mod n),
我们说n是基于a的伪素数。如果一个数是伪素数,那么它几乎肯定是素数。
Miller-Rabin测试:不断选取不超过n-1的基b(s次),计算是否每次都有b^(n-1) ≡ 1(mod n),若每次都成立则n是素数,否则为合数。
二次探测定理:如果p是奇素数,则 x^2 ≡ 1(mod p)的解为 x = 1 || x = p - 1(mod p);
代码
public long multiple(long a,long b,long n){
long ans = 0;
while(b > 0){
if((b & 1) == 1){
ans = (ans+a)%n;
}
a = (a + a)%n;
b >>= 1;
}
return ans;
}
//幂运算要借助到之前的乘法运算
public long power(long a,long b,long n){//b个a相乘,把个数b化成2的多项式的形式,
// 每次递归求出二项式的每一项,再通过位是否为1判断需不需要这一项
long ans = 1;
while(b > 0){
if((b & 1) == 1){
ans = multiple(ans,a,n);//(ans * a)mod n
}
a = multiple(a,a,n);//(a * a)mod n
b >>= 1;
}
return ans;
}
public boolean miller_rabin(int n){
if(n==2 || n==3 || n==5 || n==7 || n==11) return true;
if(n==1 || (n%2)==0 || (n%3)==0 || (n%5)==0 || (n%7)==0 || (n%11)==0) return false;
long x,pre,u;
int offset=0;
u=n-1;
while((n&1) != 0){
offset++;
n>>=1;
}
//去掉最低位1后面的0,为什么?减少x^n-1的计算量
//x的32次方要算32次,而去掉0算再乘回去只要算5次
//那x的41次方呢?101001
Random random = new Random();
//不断选取不超过n-1的x(s次),计算是否每次都有x^(n-1) ≡ 1(mod n),
//若每次都成立则n是素数,否则为合数
for(int i=0;i<8;i++){
x = random.nextInt() % (n-2) + 2;//2到n的随机数
if(x % n == 0) continue;
x = power(x,u,n);//计算x的n-1次方
pre = x;//存下来
for(int j = 0; j < offset; ++j) { //把移位减掉的量补上,并在这地方加上二次探测
x = multiple(x, x, n);
//pre=x,x=x*x
if(x == 1 && pre != 1 && pre != n-1)
return false;
//二次探测定理,这里如果x = 1则pre 必须等于 1或 n-1,否则可以判断不是素数
pre = x;
}
if(x != 1) return false; //费马小定理
}
return true;
}
题目类比:素数筛
从2开始,删除连续序列中的2的倍数,再从下一个数开始,删去它的倍数,最后剩下的数字都是素数。
对于给定区间a到b,如果a,b很大,会出现逐次检查每个数字的情况,效率低。可以选择区间0到根号b,在小区间的筛选的时候,同时删去大区间的数,就可以确保最大的数不超过根号b,比较次数减少。
代码:
public class prime_filter {
int[] prime;
boolean[] isprime;
public int sieve(int n){
prime = new int[n];//第p个素数
isprime = new boolean[n+1];//i是不是素数
int point = 0;
Arrays.fill(isprime,true);
isprime[0] = isprime[1] = false;//0,1都不是素数
for(int i=0;i<n;i++){
if(isprime[i]){
prime[point++] = i ;
for(int j = 2*i;j < n;j+=i){
isprime[j] = false;
}
}
}
return point;
}
//求区间a,b之间的素数个数,打印的话就存到arraylist
boolean[] isprime_small;
public int segment_sieve(int a,int b){
int ans = 0;
int len = b-a+1;
prime = new int[len];
isprime = new boolean[len];
//判断a-b之间的数的是不是素数,每一个元素对应原来数组的一个数
isprime_small = new boolean[(int)Math.sqrt(b)+1];
//判断0-根号b之间的数是不是素数
//对下标在a,b之间的数进行筛选
Arrays.fill(isprime,true);//0----根号b的初始化
Arrays.fill(isprime_small,true);//0----b-a的初始化
if(a == 1){
isprime[0] = false;
}//isprime[0] = isprime[1] = false
for(int i=2;i <= Math.sqrt(b);i++){
// System.out.println(Arrays.toString(isprime));
if(isprime_small[i]){
//用i筛选0----根号b
for(int j = 2*i;j <= Math.sqrt(b);j+=i){ isprime_small[j] = false; }
//用i筛选a----b
//考虑a<2的情况,此时不需要检验a处的元素
//从a之后第一个i的倍数开始,即 (a+i-1) / i
for(int j=Math.max(2,(a+i-1) / i) * i; j<=b ;j+=i){
isprime[j-a] = false;
}//isprime[i - a] = true表示i是素数
}
}
for(int i=0;i<isprime.length;i++){
if(isprime[i])
ans++;
}
for(int i=0;i< isprime.length;i++){
if(isprime[i]){
System.out.print((i+1)+",");
}
}
System.out.println();
for(int i=0;i< isprime_small.length;i++){
if(isprime_small[i]){
System.out.print((i+1)+",");
}
}
System.out.println();
return ans;
}
public static void main(String[] args) {
prime_filter demo = new prime_filter();
System.out.println(demo.sieve(100));
System.out.println(demo.segment_sieve(1,100));
}
运行结果

六、删数问题
题目
任意给定一个n位正整数a ,去掉其中任意k个数字后;剩下的数字按照原有次序排列组成的一个新的正整数b,试用贪心算法求出一个删除方案使得b值最小;
思路
贪心的删除剩余序列里最大的那个数。
对于有0的序列,0在次高位是最小的。
细节
出现0的时候如何处理:取最左边的0尾基准先删除左边的元素,如果不够再删右边的元素。
对于只剩两位数的情况,单独处理。
代码
public int solve(int a,int k){
int[] number = new int[String.valueOf(a).length()];
for(int i=number.length-1;a != 0;i--){
if(i < 0)
break;
number[i] = a%10;
a=a/10;
}
System.out.println(Arrays.toString(number));
int left = 0;
while(number[left] != 0){
left++;
}
left--;
//left是0左边第一个元素,左边删left个元素,右边删k-left个元素
//0元素的下标:left+1
k = k-left;
int partition = left+1;
if(k<=0){
left = k+left;
}//第一个0左边元素比k还要多
System.out.println(left+","+k);
while(left > 0){
int max = 0,index = 0;
for(int i=0;i<partition;i++){
if(max < number[i]){
max = number[i];
index = i;
}
}
number[index] = -1;
left--;
}
while(k > 0){
int max = 0,index = 0;
for(int i=partition+1;i<number.length;i++){
if(max <= number[i]){
max = number[i];
index = i;
}
}
if(index == 0){
number[partition] = -1;
break;
}//40
number[index] = -1;
k--;
}
int ans = 0;
for(int i=0;i<number.length;i++){
if(number[i] != -1){
ans*=10;
ans+=number[i];
}
}
System.out.println(Arrays.toString(number));
return ans;
运行结果


七、加油站问题
题目
汽车加油问题:一辆汽车加满油后可以行驶N千米,汽车从A地开往B地,途中有K个加油站,已知AB两地距离最近一个加油站的距离以及各个加油站和之间的距离(各个加油站之间的距离不完全相等)。
设计一个有效的贪心算法使沿途的加油次数最少,并指出应在哪些加油站停靠加油
思路
每次路过加油站,不加油,而是把它记录下来,当没有油的时候,从记录队列中贪心的选取油最多的加油站加油,更新当前油量,如果最后的距离大于终点,说明是可行的,输出停靠次数。
代码
int destination,prime_column,station_num;
PriorityQueue<int[]> stations;
PriorityQueue<Integer> used;
public int solve(int destination, int prime_column, int station_num,
int[] station_distance, int[] station_capacity) {
this.destination = destination;//目的地
this.prime_column = prime_column;//初始油
int[] nums = new int[station_distance.length];
for(int i=1;i<=station_distance.length;i++){
nums[i-1]=i;
}
int[][] stationInformation= new int[station_capacity.length][3];
for(int i=0;i<stationInformation.length;i++){
stationInformation[i][0] = nums[i];
stationInformation[i][1] = station_distance[i];
stationInformation[i][2] = station_capacity[i];
}
System.out.println(Arrays.deepToString(stationInformation));
stations = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[2] < o2[2] ?-1:1;
}
});
used = new PriorityQueue<>();
int ans = 0,fetch=prime_column;//fetch表示当前可达的范围
int i=0;
while(i < station_capacity.length){
while(i < station_capacity.length && stationInformation[i][1] <= fetch){
stations.add(stationInformation[i]);//不加油,而是入队
i++;
System.out.println(fetch+","+i);
}
//一开始一个都到不了,所以要不断加油
while(i < station_capacity.length &&fetch <= stationInformation[i][1]){
if(stations.isEmpty()){
return -1;
}
fetch += stations.peek()[2];
used.add(stations.peek()[0]);
stations.poll();
// System.out.println(fetch+","+i);
}
if(fetch >= destination){
break;
}
//现在能到了,把能到的所有加油站入队
System.out.println(fetch+","+i);
}
return used.size();
}
public static void main(String[] args){
int ans1 = new Expedition_PriorityQueue_加油站问题().solve(
25,
10,
4,
new int[]{10,14,20,21},
new int[]{10,5,2,4});
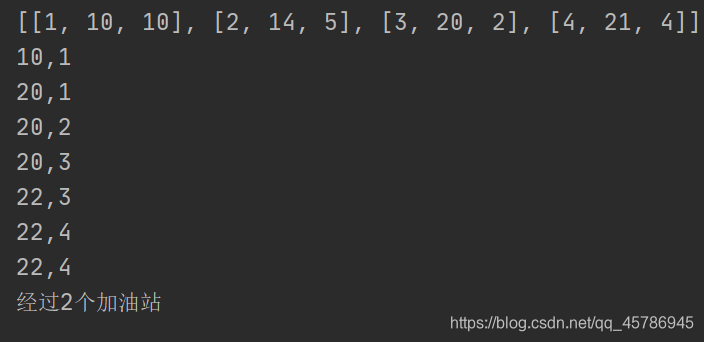
System.out.println(ans1 == -1?"不可达":"经过"+ans1+"个加油站");
}
运行结果

























 1428
1428

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










