约瑟夫问题

问题描述

Josephu(约瑟夫、约瑟夫环)  问题 Josephu  问题为：设编号为1，2，… n的n个人围坐一圈，约定编号为k（1<=k<=n）的人从1开始报数，数到m 的那个人出列，它的下一位又从1开始报数，数到m的那个人又出列，依次类

推，直到所有人出列为止，由此产生一个出队编号的序列。

举个例子

n = 5 , 即有5个人

k = 1, 从第一个人开始报数

m = 2, 数2下

经过一次出圈后

第二次出圈

第三次出圈

第四次出圈

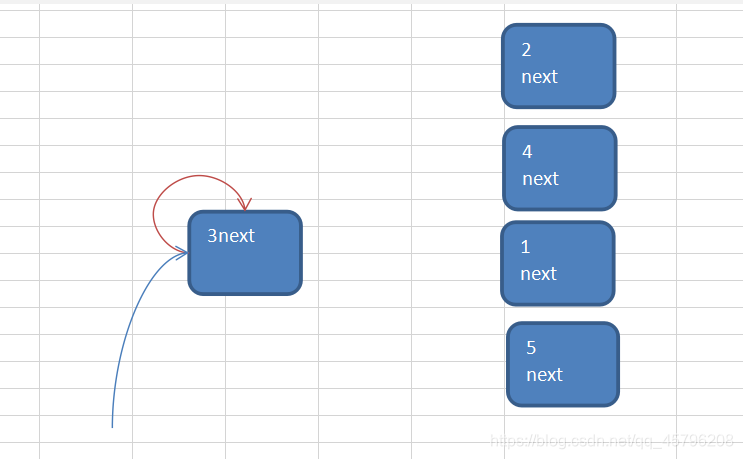
所以最终的出圈顺序 2->4->1->5->3

以上方法是使用单向循环链表来完成的，下面看代码展示

创建一个孩子类，每个孩子对象表示一个节点

class Boy{
    //小孩编号
    private int no;
    //下一个小孩
    private Boy next;

    //构造器
    public Boy(int no){
        this.no = no;
    }

    public int getNo() {
        return no;
    }

    public Boy getNext() {
        return next;
    }

    public voi