Codeforces Round 933 (Div. 3)（A,B,C,D,E,F,G）

题目链接

之前连打三把 div2，连掉三把分，终于迎来了第一个div3

这场简单，题目出的也好，C是个有点意思的思维题，D是个模拟暴力，E是单调队列优化dp，F是二分查找，G是需要稍微处理一下的 $dijkstra$。

放一下队友的题解，可以对照着看看，也许更好懂。

---

A Rudolf and the Ticket

题意：

鲁道夫要去拜访伯纳德，他决定乘地铁去找他。这张票可以在一台只接受两个硬币的机器上购买，硬币总数不超过 $k$ 。

鲁道夫有两个装硬币的口袋。

在左边的口袋里，有 $n$ 枚面额为 $b_1,b_2,\dots ,b_n$ 的硬币。在右边的口袋里，有 $m$ 枚面额为 $c_1,c_2,\dots ,c_m$ 的硬币。他想从左口袋和右口袋各选一枚硬币（共两枚）。帮助鲁道夫确定有多少种方法可以选择索引 $f$ 和 $s$ ，以便 $b_f+c_s\le k$ 。

思路：

爆搜即可，二分也行。

code：

#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=105;

int T,n,m,k;
int b[maxn],c[maxn];

int main(){
	cin>>T;
	while(T--){
		cin>>n>>m>>k;
		for(int i=1;i<=n;i++)cin>>b[i];
		for(int i=1;i<=m;i++)cin>>c[i];
		
		int cnt=0;
		for(int i=1;i<=n;i++)
			for(int j=1;j<=m;j++){
				if(b[i]+c[j]<=k)
					cnt++;
			}
		cout<<cnt<<endl;
	}
	return 0;
}

---

B. Rudolf and 121

题意：

Rudolf 有一个由 $n$ 个整数组成的数组 $a$ ，元素的编号从 $1$ 到 $n$ 。

在一次操作中，他可以选择索引 $i$ ( $2\le i\le n-1$ ) 并赋值：

• $a_{i-1}=a_{i-1}-1$
• $a_i=a_i-2$
• $a_{i+1}=a_{i+1}-1$

鲁道夫可以任意多次使用这个运算。任何索引 $i$ 都可以使用 0 次或更多次。

他能用这个运算使数组中的所有元素都等于零吗？

思路：

发现最左边的元素要变成 $0$，只能对最左边右一个元素进行操作。那么我们每次把最左边那个非 $0$ 元素变成 $0$ ，如果途中有的数不够减，变成负数了，那么就说明无解，否则最后应该所有元素都是 $0$。

code：

#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=2e5+5;

int T,n,a[maxn];

int main(){
	cin>>T;
	while(T--){
		cin>>n;
		for(int i=1;i<=n;i++)cin>>a[i];
		bool flag=true;
		for(int i=1;i<=n-2;i++){
			if(a[i]<0){
				flag=false;
				break;
			}
			a[i+1]-=a[i]*2;
			a[i+2]-=a[i];
			a[i]=0;
		}
		if(flag && a[n-1]==0 && a[n]==0)puts("YES");
		else puts("NO");
	}
	return 0;
}

---

C. Rudolf and the Ugly String

题意：

鲁道夫有一个长度为 $n$ 的字符串 $s$ 。如果字符串 $s$ 包含子串 ${}^{†}$ pie 或子串 map，鲁道夫就会认为这个字符串 $s$ 很丑。pie 或子串 map，否则字符串 $s$ 将被视为优美。

例如，ppiee、mmap、dfpiefghmap 是丑字符串，而 mathp、ppiiee 是美字符串。

Rudolf 希望通过删除一些字符来缩短字符串 $s$ 使其美观。

主角不喜欢吃力，所以他要求你删除最少的字符，使字符串变得漂亮。他可以删除字符串中任何位置的字符(不仅仅是字符串的开头或结尾)。

${}^{†}$ 如果字符串 $b$ 中存在一个连续的字符段等于 $a$ ，则字符串 $a$ 是 $b$ 的子串。

思路：

发现 map 和 pie 大部分字符都是互不相干的，这意味着如果某个连续的字符是 map，那么它就不能同时作为 pie 的一部分，我们就不需要考虑几个串杂交在一起的情况。

不过还是有例外的就是 mapie 这种情况，这时只会产生一次贡献，不过还是如上面所说，这个串也和上面两个串相差甚远，三个串不可能杂交在一起，也就是说 mapie，map，pie 两两之间不会有重合的部分。

因此我们就直接暴力枚举一个位置，看一看它满足三个串中的哪个，如果匹配上了，累加进答案后就直接跳过这片区域。

code：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

int T,n;
string s;

int main(){
	cin>>T;
	while(T--){
		cin>>n>>s;
		int cnt=0;
		for(int i=0;i<n;){
			if(i+5<=n && s.substr(i,5)=="mapie")cnt++,i+=5;
			else if(i+3<=n && s.substr(i,3)=="map")cnt++,i+=3;
			else if(i+3<=n && s.substr(i,3)=="pie")cnt++,i+=3;
			else i++;
		}
		cout<<cnt<<endl;
	}
	return 0;
}

---

D. Rudolf and the Ball Game

题意：

鲁道夫和伯纳德决定和朋友们玩一个游戏。 $n$ 人站成一圈，开始互相扔球。他们按顺时针顺序从 $1$ 到 $n$ 依次编号。

让我们把球从一个人向他的邻居移动称为一次过渡。转换可以顺时针或逆时针进行。

我们把从棋手 $y_1$ 到棋手 $y_2$ 的顺时针(逆时针)距离称为从棋手 $y_1$ 到棋手 $y_2$ 所需的顺时针(逆时针)转换次数。例如，如果是 $n=7$ ，那么从 $2$ 到 $5$ 的顺时针距离是 $3$ ，而从 $2$ 到 $5$ 的逆时针距离是 $4$ 。

初始时，球在编号为 $x$ 的棋手处(棋手按顺时针方向编号)。在第 $i$ 步时，持球人将球抛向 $r_i$ ( $1\le r_i\le n-1$ )顺时针或 $7$ ( $2$ )逆时针的距离。( $1\le r_i\le n-1$ ) 的距离顺时针或逆时针抛出。例如，如果有 $7$ 名球员，第 $2$ 名球员在接球后将球投掷到 $5$ 处，那么球将被第 $7$ 名球员(顺时针投掷)或第 $4$ 名球员(逆时针投掷)接住。该示例的图示如下。

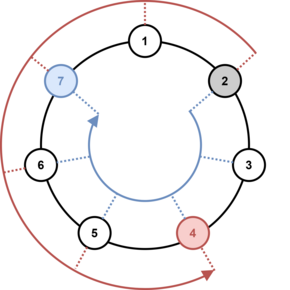
由于下雨，比赛在 $m$ 次投掷后中断。雨停后，大家又聚在一起继续比赛。但是，没有人记得球在谁手里。结果，伯纳德记住了每次投掷的距离和一些次投掷的方向(顺时针或逆时针)。

鲁道夫请你帮助他，根据伯纳德提供的信息，计算出 $m$ 次抛球后可能拿到球的球员人数。

思路：

可以跑 $nmlog(nm)$，这意味着我们可以枚举每一轮每一个人，还能有 $log$ 的处理时间。考虑直接暴力模拟传球的过程。

为了方便使用取模来模拟循环，给每个人的编号减一，使得编号是 $0\sim n-1$，这时顺时针旋转就是加 $r$ 取模，逆时针旋转就是减 $r$ 取模。

因为有的轮数中方向不确定，题目要求找到所有可能的球员，所以需要把两种方向的所有可能的球员都算出来。正常来说最坏情况每轮人数乘以 $2$，空间和时间很快都会爆掉。但是发现总人数总共就是 $n$ ，因此同时去重的话，每轮暴力模拟的时间复杂度最坏是 $nlogn$ 的。因此使用 set 存储。

code：

#include <iostream>
#include <cstdio>
#include <set>
#include <cstring>
using namespace std;

int T,n,m,x;


int main(){
	cin>>T;
	while(T--){
		cin>>n>>m>>x;
		set<int> s,t;
		s.insert(x-1);
		for(int i=1,dis;i<=m;i++){
			string st;
			cin>>dis>>st;
			if(st=="0"){
				for(auto tmp:s)
					t.insert((tmp+dis)%n);
			}
			else if(st=="1"){
				for(auto tmp:s)
					t.insert((tmp-dis+n)%n);
			}
			else {
				for(auto tmp:s){
					t.insert((tmp+dis)%n);
					t.insert((tmp-dis+n)%n);
				}
			}
			s=t;
			t.clear();
		}
		cout<<s.size()<<endl;
		for(auto x:s)cout<<x+1<<" ";
		cout<<endl;
	}
	return 0;
}

---

E. Rudolf and k Bridges

题意：

伯纳德喜欢拜访鲁道夫，但他总是迟到。问题是伯纳德必须乘渡船过河。鲁道夫决定帮助他的朋友解决这个问题。

这条河是由 $n$ 行和 $m$ 列组成的网格。第 $i$ 行和第 $j$ 列的交点包含数字 $a_{i,j}$——相应单元格的深度。第一列和最后列中的所有单元格都与河岸相对应，因此它们的深度为 $0$ 。

比如河流可能是这样的。

鲁道夫可以选择第 $(i,1),(i,2),\dots ,(i,m)$ 行，并在上面建造一座桥。在该行的每个单元格中，他都可以为桥安装一个支架。在第 $(i,j)$ 格安装支架的成本为 $a_{i,j}+1$ 。安装支架必须满足以下条件：

1. 必须在单元格 $(i,1)$ 中安装一个支架；
2. 单元格 $(i,m)$ 中必须安装一个支架；
3. 任何一对相邻支架之间的距离不得大于 $d$ 。

只建一座桥是很无聊的。因此，鲁道夫决定在河的连续行上建造 $k$ 座桥，也就是选择一些 $i$ ( $1\le i\le n-k+1$ )，独立地建造一座桥。( $1\le i\le n-k+1$ )，并在每一行 $i,i+1,\dots ,i+k-1$ 上独立建造一座桥。帮助鲁道夫最小化安装支架的总成本。

思路：

发现每一行之间修建的代价都互不影响，如果我们算出来了每一行的代价，剩下的就是跑一遍前缀和，然后找到代价最小的区间和就行了。所以问题就转化为了给你一行 $m$ 个数，问怎么修建支架，使得满足条件的同时代价最小。

比较容易看出来这个是个比较裸的动态规划。如果位置 $i$ 修支架，那么区间上 $[i-d-1,i-1]$ 必须至少存在一个支架，设 $dp[i]$ 为在位置 $i$ 修支架并且前 $i$ 个位置满足条件的最小代价，那么 $dp[i]$ 可以从 $dp[j](i-d-1\le j\le i-1)$ 推过来。而我们要找到区间 $[i-d-1,i-1]$ 上的最小 $dp$ 值，这就很滑动窗口了，可以单调队列实现（虽然我第一眼没看出来，写的双set）。

不过这个题的优化思路其实很多，可以用双set，单调队列，也可以用优先队列。不过单调队列会少个 $log$

code：

双set优化

#include <iostream>
#include <cstdio>
#include <vector>
#include <set>
#define mk make_pair
using namespace std;
typedef long long ll;
const int maxn=105;
const int maxm=2e5+5;
const ll inf=1e18;


int T,n,m,k,d;
int a[maxm];
ll dp[maxm];

ll cost[maxn];

int main(){
	cin>>T;
	while(T--){
		cin>>n>>m>>k>>d;
		for(int bridge=1;bridge<=n;bridge++){
			for(int i=1;i<=m;i++)cin>>a[i],dp[i]=inf;
			set<pair<ll,ll> > s1,s2;
			
			dp[1]=1;
			s1.insert(mk(1,1));
			s2.insert(mk(1,1));
			for(int i=2;i<=m;i++){
				dp[i]=min(dp[i],s1.begin()->first+a[i]+1);
				s1.insert(mk(dp[i],i));
				s2.insert(mk(i,dp[i]));
				if(i-d>s2.begin()->first){
					s1.erase(mk(s2.begin()->second,s2.begin()->first));
					s2.erase(s2.begin());
				}
			}
//			cout<<dp[m]<<endl;
			
			cost[bridge]=cost[bridge-1]+dp[m];
		}
		ll ans=inf;
		for(int i=k;i<=n;i++)
			ans=min(ans,cost[i]-cost[i-k]);
		cout<<ans<<endl;
	}
	return 0;
}

单调队列

#include <iostream>
#include <cstdio>
#include <vector>
#include <set>
#include <queue>
#define mk make_pair
using namespace std;
typedef long long ll;
const int maxn=105;
const int maxm=2e5+5;
const ll inf=1e18;

int T,n,m,k,d;
int a[maxm];
ll dp[maxm];

ll cost[maxn];

int main(){
	cin>>T;
	while(T--){
		cin>>n>>m>>k>>d;
		for(int bridge=1;bridge<=n;bridge++){
			for(int i=1;i<=m;i++)cin>>a[i],dp[i]=inf;
			deque<pair<ll,ll> > q;
			
			dp[1]=1;
			q.push_back(mk(1,1));
			for(int i=2;i<=m;i++){
				dp[i]=min(dp[i],q.front().first+a[i]+1);
				while(!q.empty() && dp[i]<=q.back().first)q.pop_back();
				q.push_back(mk(dp[i],i));
				if(i-d>q.front().second)q.pop_front();
			}
//			cout<<dp[m]<<endl;
			
			cost[bridge]=cost[bridge-1]+dp[m];
		}
		ll ans=inf;
		for(int i=k;i<=n;i++)
			ans=min(ans,cost[i]-cost[i-k]);
		cout<<ans<<endl;
	}
	return 0;
}

实际上哪种优化方法都是大差不差，我队友写的优先队列，想看可以去翻他的。链接在文章开头。

---

F. Rudolf and Imbalance

题意：

鲁道夫准备了一组复杂度为 $a_1<a_2<a_3<\cdots <a_n$ 的 $n$ 问题。他对均衡性并不完全满意，因此想只增加一个问题来解决它。

为此，鲁道夫提出了 $m$ 个问题模型和 $k$ 个函数。 $i$ 个模型的复杂度是 $d_i$ ， $j$ 个函数的复杂度是 $f_j$ 。要创建一个问题，他需要选择值 $i$ 和 $j$ ( $1\le i\le m$ ， $1\le j\le k$ ， $i$ )。( $1\le i\le m$ , $1\le j\le k$ )，将第 $i$ 个模型与第 $j$ 个函数相结合，就会得到一个复杂度为 $d_i+f_j$ 的新问题。

为了确定集合的不平衡性，鲁道夫将问题的复杂度按升序排序，并找出 $a_i-a_{i-1}$ ( $i>1$ )的最大值。

鲁道夫根据上述规则最多增加一个问题所能达到的最小不平衡值是多少？

思路：

上面扯了这么多，其实很简单，就是从 $f,d$ 数组中各取一个数，并把它们的和加入数组 $a$，问最小的最大差值是多少。

不难想到，我们要得到最小的最大差值，肯定要把最大差值给拆了，否则拆其他差值，最大差值还在，最大差值并不会减小。而如果我们成功把最大差值拆掉了，得到的新最大差值，有可能是最大差值被拆成两部分中的较大部分，抑或是原本数组中的次大差值。次大差值不会变，可以直接找到，所以这个题就转化成了求出最大差值最平均的拆法（这时两部分中的较大部分就会较小）。

发现需要 $nlogn$ 的做法。枚举两个数组是没可能的。一般这种情况都是枚举其中一个数组，然后再用 $logn$ 的时间去另一个数组进行查找。考虑如何找到这个最平分最大差值的值，如果 $a_i-a_{i+1}$ 得到最大差值，$f$ 数组枚举到了第 $j$ 个，那么我们希望得到的和应该是 $\frac{a_i+a_{i+1}}{2}$ ，但是在 $d$ 数组中不一定找得到 $\frac{a_i+a_{i+1}}{2}-f_i$ 这个值，如果向外一个数一个数的枚举，最坏情况会 $T$。

那怎么办呢，因为其实对 $f_i$，如果要从 $d$ 数组中找到某个值，使得它们的和最接近 $\frac{a_i+a_{i+1}}{2}$，我们在 $d$ 中要找的其实就是离 $\frac{a_i+a_{i+1}}{2}-f_i$ 最近的两个值（一个大于 $\frac{a_i+a_{i+1}}{2}-f_i$，一个小于它）。我们直接在 $d$ 数组中二分查找第一个大于等于 $\frac{a_i+a_{i+1}}{2}-f_i$ 的值，然后它前面那个值和这个值就是上面说的离 $\frac{a_i+a_{i+1}}{2}-f_i$ 最近的两个值了。

找到之后，看一下哪个拆出来的最大差值更小即可。

code：

#include <iostream>
#include <cstdio>
#include <set>
using namespace std;
typedef long long ll;
const int maxn=2e5+5;

int T,n,m,k;
ll a[maxn],L,R,len,len2;
set<ll> f,d;

int main(){
	cin>>T;
	while(T--){
		cin>>n>>m>>k;
		len=len2=0;
		f.clear();
		d.clear();
		for(int i=1;i<=n;i++){
			cin>>a[i];
			if(i>1){
				if(len<=a[i]-a[i-1]){
					len2=len;
					len=a[i]-a[i-1];
					L=a[i-1];R=a[i];
				}
				else if(len2<a[i]-a[i-1])len2=a[i]-a[i-1];
			}
		}
//		cout<<len<<" "<<len2<<endl;
		for(int i=1,t;i<=m;i++){
			cin>>t;
			f.insert(t);
		}
		for(int i=1,t;i<=k;i++){
			cin>>t;
			d.insert(t);
		}
		ll ans=len;
		for(auto x:f){
			auto it=d.lower_bound((L+R)/2-x),it1=it,it2=it;
			ans=min(ans,max(*it+x-L,R-x-*it));
			if(it1!=d.begin()){
				it1--;
				ans=min(ans,max(*it1+x-L,R-x-*it1));
			}
		}
		cout<<max(len2,ans)<<endl;
	}
	return 0;
}

---

G. Rudolf and Subway

题意：

造桥并没有帮到伯纳德，他到哪儿都迟到。后来，鲁道夫决定教他乘地铁。

鲁道夫把地铁图描绘成了一个没有自循环的无向连通图，图中的顶点代表车站。任意一对顶点之间最多只有一条边。

如果可以绕过其他车站直接到达相应的车站，则两个顶点之间有一条边相连。鲁道夫和伯纳德所在城市的地铁采用了彩色符号。这意味着站点之间的任何一条边都有特定的颜色。特定颜色的边共同组成一条地铁线。地铁线不能包含不连接的边，并构成给定地铁图的连接子图。

地铁图的示例如图所示。

鲁道夫认为，如果经过的地铁线路数量最少，那么这条线路就是最优的。

请帮助伯纳德确定给定出发站和终点站的最少线路数。

思路：

发现如果我们经过某条地铁线路到达了某个点，那么我们就可以无代价地到达同一线路的其他点。一开始的思路是跑一个耿直的 $dijkstra$，然后在优先队列里的每个状态额外存储一个上一步经过哪条线路，但是这是有bug的。比如到达某个关键点的时候是某个线路先到，然后vis数组标记了这个车站，后来的某些线路就不能更新这个车站了，也就没法再次进入优先队列，后续通过这条线路来更新答案也就没戏了。

举个例子，输入：

4 4
1 2 1
1 3 2
2 3 1
3 4 1

如果通过上面的思路，有可能通过线路 $2$ 更新了车站 $3$ 的距离，并把状态加入了优先队列，之后通过线路 $1$ 到达车站 $3$ 的时候，就不能更新车站 $3$ 的答案了，也就无法进入优先队列，但是后面的车站 $4$ 需要坐线路 $1$ 才能最短地到达。

发现这个bug是无法解决的。只能另寻他路。因此我们可以尝试对线路上每个点互相之间建立一条捷径，不过直接建立捷径的话没法保证上一次是经过同一条线路，所以我们在建立捷径的时候可以给出 $1$ 的代价，或者建立一个中转点，进入中转点的时候需要支付 $1$ 的代价，返回的时候不需要。因为前者最坏是 $O(n^2)$ 的复杂度，所以我们使用中转点的做法。

之后就是普通的 $dijkstra$ 啦。

code：

奇妙的RE，所以多开了一倍的空间。

#include <iostream>
#include <cstdio>
#include <queue>
#include <vector>
#include <map>
#include <set>
#define mk make_pair
using namespace std;
const int maxn=2e5+5; 
const int inf=1e9;

int T,n,m;
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
int d[maxn<<2];
bool vis[maxn<<2];

int head[maxn<<1],cnt;
struct edge{
	int v,w,nxt;
}e[maxn<<3];
void add(int u,int v,int w){
	e[++cnt].v=v;
	e[cnt].w=w;
	e[cnt].nxt=head[u];
	head[u]=cnt;
}

int st,ed;

int color;
set<int> t[maxn];
map<int,int> mp;

int main(){
	cin>>T;
	while(T--){
		cin>>n>>m;
		for(int i=1;i<=2*n+5;i++)head[i]=0;
		cnt=0;
		color=0;
		mp.clear();
		for(int i=1,u,v,c;i<=m;i++){
			cin>>u>>v>>c;
			add(u,v,1);
			add(v,u,1);
			if(mp.find(c)==mp.end())mp[c]=++color;
			t[mp[c]].insert(u);
			t[mp[c]].insert(v);
		}
		for(int i=1;i<=color;i++){
			for(auto u:t[i]){
				add(n+i,u,1);
				add(u,n+i,0);
			}
			t[i].clear();
		}
		cin>>st>>ed;
		
		for(int i=1;i<=2*n+5;i++)d[i]=inf,vis[i]=false;
		while(!q.empty())q.pop();
		d[st]=0;
		q.push(mk(d[st],st));
		while(!q.empty()){
			int u=q.top().second;
			q.pop();
//			cout<<u<<endl;
			if(u==ed)break;
			if(vis[u])continue;
			else vis[u]=true;
//			cout<<u<<endl;
			for(int i=head[u],v,w;i;i=e[i].nxt){
				v=e[i].v;
				w=e[i].w;
				if(d[v]>=d[u]+w){
					d[v]=d[u]+w;
					q.push(mk(d[v],v));
				}
			}
		}
		
//		for(int i=1;i<=n;i++)cout<<d[i]<<" ";
//		cout<<endl;
		cout<<d[ed]<<endl;
	}
	return 0;
}