求解一维Sod激波管问题

最新推荐文章于 2024-04-26 16:55:17 发布

qq_45885422

最新推荐文章于 2024-04-26 16:55:17 发布

阅读量7.6k

点赞数 30

文章标签： matlab

本文链接：https://blog.csdn.net/qq_45885422/article/details/121269417

版权

本文是计算流体力学课程的大作业项目，全文基于Matlab代码编写，希望能够给相关专业的同学提供一些帮助。课程作业分为一维Sod激波管问题编程计算和自选具体流动问题的软件数值模拟两个选题。第一个选题其问题描述如下：

$x\in [0,1]$

$t=0:\quad(\rho ,u,p)=\left\{\begin{matrix} 1,0,1\quad x< 0.5\\ 0.125,0,0.1 \quad x\geq 0.5\end{matrix}\right.$

在查找资料时，发现网上已有很多现成可用的代码，而我在本科时接触的比较多的是CFD，想特别一些，因此在查论文时，发现了一些可用的方法，相当于复刻论文了。本文基于张涵信院士提出的NND计算格式，采用Steger_Warming矢通量分裂方法。张涵信院士是我国计算流体力学开创者和奠基人之一，长期致力于结合物理分析的计算流体力学理论和应用研究，为我国航空航天事业作出突出贡献。

1.理论推导

一维流动欧拉方程：

$\frac{\partial \textbf{U} }{\partial t}+\frac{\partial \textbf{f} }{\partial x}=0$

其中 $\textbf{U}=\begin{bmatrix} \rho & \rho u & \rho E \end{bmatrix}^{T}$ ， $\textbf{f}=\begin{bmatrix} \rho u& \rho u^{2} +p& \rho u E+pu \end{bmatrix}^{T}$ ， $E=e+\frac{u^{2}}{2}$

其特征根为 $\lambda_{1} =u$ ， $\lambda_{2} =u+c$ ， $\lambda_{3} =u-c$

空间离散构造迎风格式，引入

$\textbf{f}=f^{+}+f^{-}$

因此

$\frac{\partial \textbf{U} }{\partial t}+\frac{\partial f^{+} }{\partial x}+\frac{\partial f^{-} }{\partial x}=0$

时间离散构造一阶向前差分格式

$U_{i}^{n+1}=U_{i}^{n}-\frac{\Delta t}{\Delta x}(f_{i}^{+}+f_{i}^{-})$

按Steger_Warming矢通量分裂方法，通量项可写为

$\textbf{f}= \frac{\rho}{2\gamma }\begin{bmatrix} 2(\gamma -1)\lambda _{1}+\lambda _{2}+\lambda _{3}\\ 2(\gamma -1)\lambda _{1}u+\lambda _{2}(u+c)+\lambda _{3}(u-c)\\ (\gamma -1)\lambda _{1}u^{2}+\frac{(3-\gamma)(\lambda _{2}+\lambda _{3})c^{2}}{2(\gamma -1)}+\frac{\lambda _{2}(u+c)^{2}}{2}+\frac{\lambda _{3}(u-c)^{2}}{2} \end{bmatrix}$

当 $\lambda _{i}\geq 0$ 时， $\lambda _{i}=\lambda _{i}$ ，否则 $\lambda _{i}=0$ ，得到 $f^{+}$

当 $\lambda _{i}< 0$ 时， $\lambda _{i}=\lambda _{i}$ ，否则 $\lambda _{i}=0$ ，得到 $f^{-}$

采用NND格式改写通量项，因此

$U_{i}^{n+1}=U_{i}^{n}-\frac{\Delta t}{\Delta x}(f_{i}^{+n}+0.5min \ mod(\Delta f_{i-\frac{1}{2}}^{+n},\Delta f_{i+\frac{1}{2}}^{+n})+ f_{i+1}^{-n}-0.5min \ mod(\Delta f_{i+\frac{1}{2}}^{-n},\Delta f_{i+\frac{3}{2}}^{-n})-f_{i-1}^{+n}-0.5min \ mod(\Delta f_{i-\frac{3}{2}}^{+n},\Delta f_{i-\frac{1}{2}}^{+n})-f_{i}^{-n}+0.5min \ mod(\Delta f_{i-\frac{1}{2}}^{-n},\Delta f_{i+\frac{1}{2}}^{-n}))$

其中

$\Delta f_{i-\frac{1}{2}}^{\pm n}=f_{i}^{\pm n}-f_{i-1}^{\pm n}$

$\Delta f_{i-\frac{3}{2}}^{\pm n}=f_{i-1}^{\pm n}-f_{i-2}^{\pm n}$

定义

$min\ mod(x,y)=\left\{\begin{matrix} 0, \quad xy\leq 0\\ sign(x)\min(\left | x \right |,\left | y \right |),\quad xy> 0 \end{matrix}\right.$

2.编程实现

整体流程如下：

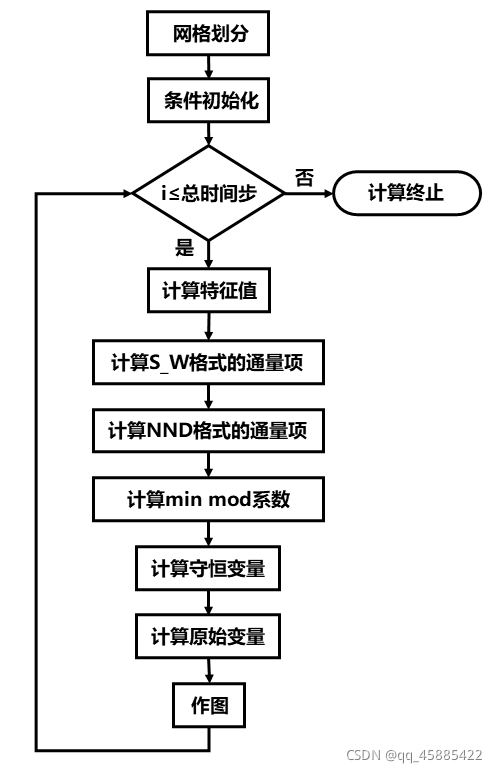
1.网格划分

跟所有求解方法相同，第一步先初始化网格，网格尺寸和时间步长的大小会影响收敛性，需要根据Courant数来约束。

delta_x=0.001;%设定网格尺寸
delta_t=0.0002;%根据Courant数设定时间步长
time_step=1/delta_t;%设定迭代时间步数
lenght_l=0.5;%给定左边管道长度
lenght_r=0.5;%给定右边管道长度
n_l=lenght_l/delta_x;%给定左边管道网格数
n_r=lenght_r/delta_x;%给定右边管道网格数

2.流场初始化

初始化我们需要的常数、守恒变量和原始变量。

gama=1.4;
p=[ones(1,n_l) 0.1*ones(1,n_r)];%初始化压力场
psi=[ones(1,n_l) 0.125*ones(1,n_r)];%初始化密度场
u=zeros(1,n_l+n_r);%初始化速度场
mass=psi.*u;%初始化质量流率
e=p./(gama-1)+0.5*psi.*u.^2;%初始化能量场

3.计算声速和特征值

c=sqrt(gama*p./psi);%计算声速
lamda1=u;%计算特征值1
lamda2=u+c;%计算特征值2
lamda3=u-c;%计算特征值3

4.根据Steger_Warming矢通量分裂计算守恒量的通量项

F_plus(1,:)=psi./(2*gama).*(2*(gama-1)*max(lamda1,0)+max(lamda2,0)+max(lamda3,0));
F_plus(2,:)=psi./(2*gama).*(2*(gama-1)*max(lamda1,0).*u+max(lamda2,0).*(u+c)+max(lamda3,0).*(u-c));
F_plus(3,:)=psi./(2*gama).*((gama-1)*max(lamda1,0).*u.^2+(3-gama)/(2*(gama-1))*(max(lamda2,0)+max(lamda3,0)).*c.^2+0.5*max(lamda2,0).*(u+c).^2+0.5*max(lamda3,0).*(u-c).^2);

F_minus(1,:)=psi./(2*gama).*(2*(gama-1)*min(lamda1,0)+min(lamda2,0)+min(lamda3,0));
F_minus(2,:)=psi./(2*gama).*(2*(gama-1)*min(lamda1,0).*u+min(lamda2,0).*(u+c)+min(lamda3,0).*(u-c));
F_minus(3,:)=psi./(2*gama).*((gama-1)*min(lamda1,0).*u.^2+(3-gama)/(2*(gama-1))*(min(lamda2,0)+min(lamda3,0)).*c.^2+0.5*min(lamda2,0).*(u+c).^2+0.5*min(lamda3,0).*(u-c).^2);

5.根据NND格式计算守恒量的通量项

for m=3:n_l+n_r-2
    for j=1:3
        F_plus_minus_1(j,m)=F_plus(j,m)-F_plus(j,m-1);
        F_minus_minus_1(j,m)=F_minus(j,m)-F_minus(j,m-1);
        
        F_plus_plus_1(j,m)=F_plus(j,m+1)-F_plus(j,m);
        F_minus_plus_1(j,m)=F_minus(j,m+1)-F_minus(j,m);
        
        F_plus_minus_3(j,m)=F_plus(j,m-1)-F_plus(j,m-2);
        F_minus_minus_3(j,m)=F_minus(j,m-1)-F_minus(j,m-2);
        
        F_plus_plus_3(j,m)=F_plus(j,m+2)-F_plus(j,m+1);
        F_minus_plus_3(j,m)=F_minus(j,m+2)-F_minus(j,m+1);
    end
end

6.计算min mod系数

x1=(sign(F_plus_minus_1)==sign(F_plus_plus_1));
x2=(sign(F_minus_plus_1)==sign(F_minus_plus_3));
x3=(sign(F_plus_minus_3)==sign(F_plus_minus_1));
x4=(sign(F_minus_minus_1)==sign(F_minus_plus_1));

7.迭代计算每个时间步的守恒量和原始量

for m=3:n_l+n_r-2
    psi(m)=psi(m)-delta_t/delta_x*(F_plus(1,m)+0.5*x1(1,m)*sign(F_plus_minus_1(1,m))*min(abs(F_plus_minus_1(1,m)),abs(F_plus_plus_1(1,m)))...
        +F_minus(1,m+1)-0.5*x2(1,m)*sign(F_minus_plus_1(1,m))*min(abs(F_minus_plus_1(1,m)),abs(F_minus_plus_3(1,m)))...
        -F_plus(1,m-1)-0.5*x3(1,m)*sign(F_plus_minus_3(1,m))*min(abs(F_plus_minus_3(1,m)),abs(F_plus_minus_1(1,m)))...
        -F_minus(1,m)+0.5*x4(1,m)*sign(F_minus_minus_1(1,m))*min(abs(F_minus_minus_1(1,m)),abs(F_minus_plus_1(1,m))));
    
    mass(m)=mass(m)-delta_t/delta_x*(F_plus(2,m)+0.5*x1(2,m)*sign(F_plus_minus_1(2,m))*min(abs(F_plus_minus_1(2,m)),abs(F_plus_plus_1(2,m)))...
        +F_minus(2,m+1)-0.5*x2(2,m)*sign(F_minus_plus_1(2,m))*min(abs(F_minus_plus_1(2,m)),abs(F_minus_plus_3(2,m)))...
        -F_plus(2,m-1)-0.5*x3(2,m)*sign(F_plus_minus_3(2,m))*min(abs(F_plus_minus_3(2,m)),abs(F_plus_minus_1(2,m)))...
        -F_minus(2,m)+0.5*x4(2,m)*sign(F_minus_minus_1(2,m))*min(abs(F_minus_minus_1(2,m)),abs(F_minus_plus_1(2,m))));
    
    u(m)=mass(m)/psi(m);
    
    e(m)=e(m)-delta_t/delta_x*(F_plus(3,m)+0.5*x1(3,m)*sign(F_plus_minus_1(3,m))*min(abs(F_plus_minus_1(3,m)),abs(F_plus_plus_1(3,m)))...
        +F_minus(3,m+1)-0.5*x2(3,m)*sign(F_minus_plus_1(3,m))*min(abs(F_minus_plus_1(3,m)),abs(F_minus_plus_3(3,m)))...
        -F_plus(3,m-1)-0.5*x3(3,m)*sign(F_plus_minus_3(3,m))*min(abs(F_plus_minus_3(3,m)),abs(F_plus_minus_1(3,m)))...
        -F_minus(3,m)+0.5*x4(3,m)*sign(F_minus_minus_1(3,m))*min(abs(F_minus_minus_1(3,m)),abs(F_minus_plus_1(3,m))));
    
    p(m)=(gama-1)*(e(m)-0.5*psi(m)*u(m)^2);
end

8.根据每个时间步作图

x=linspace(0,1,n_l+n_r);
axis([0 1 0 1]);
plot(x,psi,x,u,x,p,'LineWidth', 2);
legend('psi', 'u', 'p');
title({'Riemann Problem Solution';['t=',num2str(delta_t*i),'s']});
pause(0.0001);

9.迭代计算

不断重复3-8步骤的过程，就可以得到随时间变化的结果了。

for i=1:time_step %计算每个时间步的各个场

    3-8步骤的代码

end

3.计算结果及完整代码

3.1 计算结果

运行上述代码，可以得到本文基于Steger_Warming矢通量分裂的NND格式求解一维Sod激波管问题的结果图：

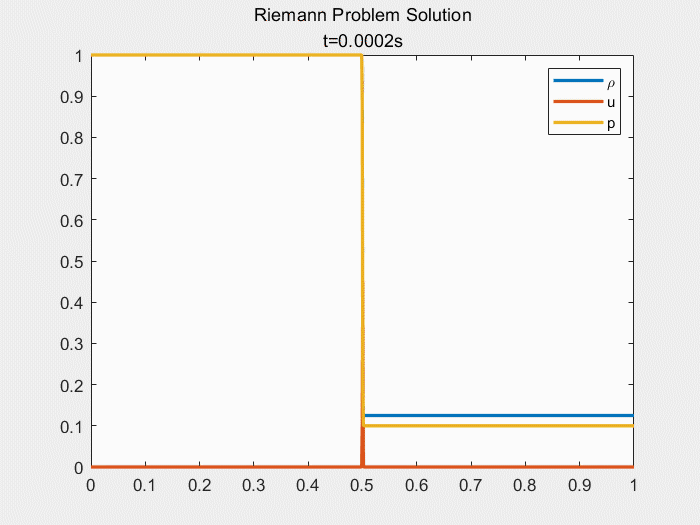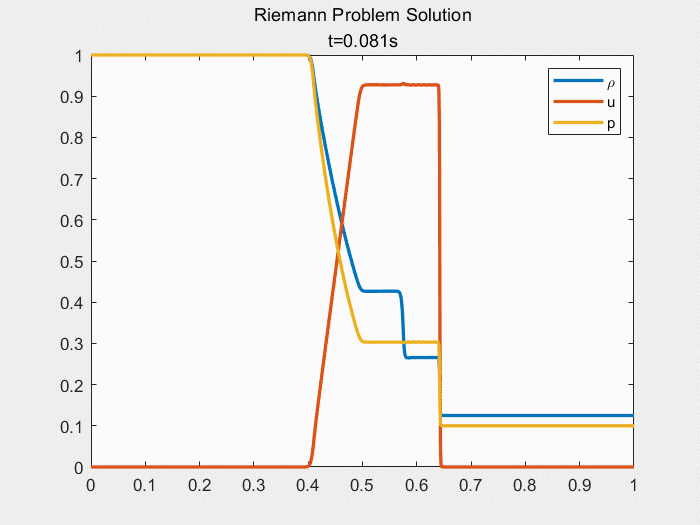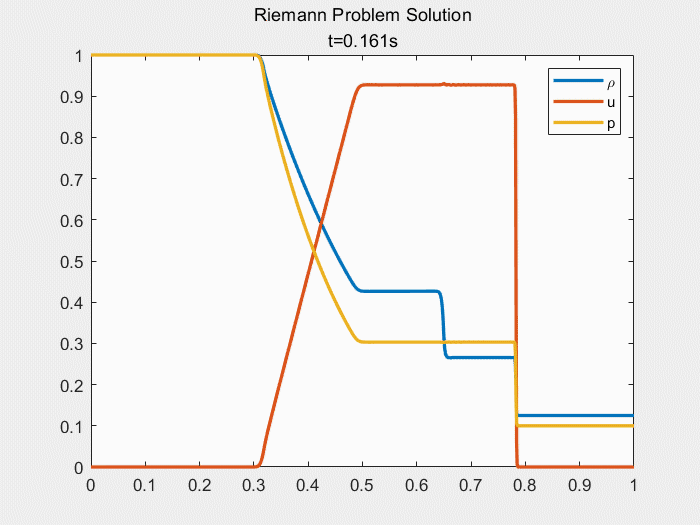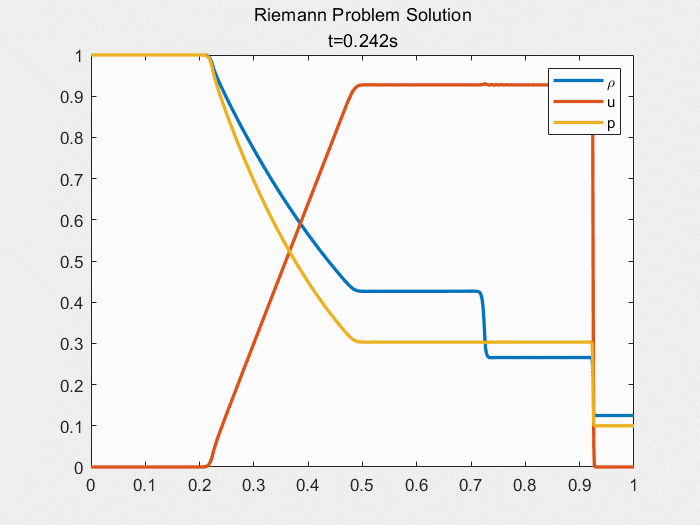
可根据结果图中判断此边界条件下一维Sod激波管的间断组合为：膨胀波—接触间断—激波。

结合Riemann问题解析解，可以对比该种方法得到的结果的准确性、振荡性和收敛性好坏，此处省略。

3.2完整代码

clc;clear all;

%%%%%%%网格划分%%%%%%%
delta_x=0.001;%设定网格尺寸
delta_t=0.0002;%根据Courant数设定时间步长
time_step=1/delta_t;%设定迭代时间步数
lenght_l=0.5;%给定左边管道长度
lenght_r=0.5;%给定右边管道长度
n_l=lenght_l/delta_x;%给定左边管道网格数
n_r=lenght_r/delta_x;%给定右边管道网格数

%%%%%%%条件初始化%%%%%%%
gama=1.4;
p=[ones(1,n_l) 0.1*ones(1,n_r)];%初始化压力场
psi=[ones(1,n_l) 0.125*ones(1,n_r)];%初始化密度场
u=zeros(1,n_l+n_r);%初始化速度场
mass=psi.*u;%初始化质量流率
e=p./(gama-1)+0.5*psi.*u.^2;%初始化能量场

%%%%%%%迭代计算%%%%%%%
for i=1:time_step %计算每个时间步的各个场
    
    c=sqrt(gama*p./psi);%计算声速
    lamda1=u;%计算特征值
    lamda2=u+c;%计算特征值
    lamda3=u-c;%计算特征值
    
    %%%根据Steger_Warming矢通量分裂计算守恒量的通量项%%%
    F_plus(1,:)=psi./(2*gama).*(2*(gama-1)*max(lamda1,0)+max(lamda2,0)+max(lamda3,0));
    F_plus(2,:)=psi./(2*gama).*(2*(gama-1)*max(lamda1,0).*u+max(lamda2,0).*(u+c)+max(lamda3,0).*(u-c));
    F_plus(3,:)=psi./(2*gama).*((gama-1)*max(lamda1,0).*u.^2+(3-gama)/(2*(gama-1))*(max(lamda2,0)+max(lamda3,0)).*c.^2+0.5*max(lamda2,0).*(u+c).^2+0.5*max(lamda3,0).*(u-c).^2);
    
    F_minus(1,:)=psi./(2*gama).*(2*(gama-1)*min(lamda1,0)+min(lamda2,0)+min(lamda3,0));
    F_minus(2,:)=psi./(2*gama).*(2*(gama-1)*min(lamda1,0).*u+min(lamda2,0).*(u+c)+min(lamda3,0).*(u-c));
    F_minus(3,:)=psi./(2*gama).*((gama-1)*min(lamda1,0).*u.^2+(3-gama)/(2*(gama-1))*(min(lamda2,0)+min(lamda3,0)).*c.^2+0.5*min(lamda2,0).*(u+c).^2+0.5*min(lamda3,0).*(u-c).^2);
    
    
    %%%结合NND格式计算守恒量的通量项%%%
    for m=3:n_l+n_r-2
        for j=1:3
            
            F_plus_minus_1(j,m)=F_plus(j,m)-F_plus(j,m-1);
            F_minus_minus_1(j,m)=F_minus(j,m)-F_minus(j,m-1);
            
            F_plus_plus_1(j,m)=F_plus(j,m+1)-F_plus(j,m);
            F_minus_plus_1(j,m)=F_minus(j,m+1)-F_minus(j,m);
            
            F_plus_minus_3(j,m)=F_plus(j,m-1)-F_plus(j,m-2);
            F_minus_minus_3(j,m)=F_minus(j,m-1)-F_minus(j,m-2);
            
            F_plus_plus_3(j,m)=F_plus(j,m+2)-F_plus(j,m+1);
            F_minus_plus_3(j,m)=F_minus(j,m+2)-F_minus(j,m+1);
            
        end
    end
    
    %%%计算min mod系数，简化方程复杂度%%%
    x1=(sign(F_plus_minus_1)==sign(F_plus_plus_1));
    x2=(sign(F_minus_plus_1)==sign(F_minus_plus_3));
    x3=(sign(F_plus_minus_3)==sign(F_plus_minus_1));
    x4=(sign(F_minus_minus_1)==sign(F_minus_plus_1));
    
    %%%迭代计算每个时间步的守恒量%%%
    for m=3:n_l+n_r-2
        
        psi(m)=psi(m)-delta_t/delta_x*(F_plus(1,m)+0.5*x1(1,m)*sign(F_plus_minus_1(1,m))*min(abs(F_plus_minus_1(1,m)),abs(F_plus_plus_1(1,m)))...
            +F_minus(1,m+1)-0.5*x2(1,m)*sign(F_minus_plus_1(1,m))*min(abs(F_minus_plus_1(1,m)),abs(F_minus_plus_3(1,m)))...
            -F_plus(1,m-1)-0.5*x3(1,m)*sign(F_plus_minus_3(1,m))*min(abs(F_plus_minus_3(1,m)),abs(F_plus_minus_1(1,m)))...
            -F_minus(1,m)+0.5*x4(1,m)*sign(F_minus_minus_1(1,m))*min(abs(F_minus_minus_1(1,m)),abs(F_minus_plus_1(1,m))));
        
        mass(m)=mass(m)-delta_t/delta_x*(F_plus(2,m)+0.5*x1(2,m)*sign(F_plus_minus_1(2,m))*min(abs(F_plus_minus_1(2,m)),abs(F_plus_plus_1(2,m)))...
            +F_minus(2,m+1)-0.5*x2(2,m)*sign(F_minus_plus_1(2,m))*min(abs(F_minus_plus_1(2,m)),abs(F_minus_plus_3(2,m)))...
            -F_plus(2,m-1)-0.5*x3(2,m)*sign(F_plus_minus_3(2,m))*min(abs(F_plus_minus_3(2,m)),abs(F_plus_minus_1(2,m)))...
            -F_minus(2,m)+0.5*x4(2,m)*sign(F_minus_minus_1(2,m))*min(abs(F_minus_minus_1(2,m)),abs(F_minus_plus_1(2,m))));
        
        u(m)=mass(m)/psi(m);
        
        e(m)=e(m)-delta_t/delta_x*(F_plus(3,m)+0.5*x1(3,m)*sign(F_plus_minus_1(3,m))*min(abs(F_plus_minus_1(3,m)),abs(F_plus_plus_1(3,m)))...
            +F_minus(3,m+1)-0.5*x2(3,m)*sign(F_minus_plus_1(3,m))*min(abs(F_minus_plus_1(3,m)),abs(F_minus_plus_3(3,m)))...
            -F_plus(3,m-1)-0.5*x3(3,m)*sign(F_plus_minus_3(3,m))*min(abs(F_plus_minus_3(3,m)),abs(F_plus_minus_1(3,m)))...
            -F_minus(3,m)+0.5*x4(3,m)*sign(F_minus_minus_1(3,m))*min(abs(F_minus_minus_1(3,m)),abs(F_minus_plus_1(3,m))));
        
        p(m)=(gama-1)*(e(m)-0.5*psi(m)*u(m)^2);
        
    end
    %%%根据每个时间步作图%%%
    x=linspace(0,1,n_l+n_r);
    axis([0 1 0 1]);
    plot(x,psi,x,u,x,p,'LineWidth', 2);
    legend('psi', 'u', 'p');
    title({'Riemann Problem Solution';['t=',num2str(delta_t*i),'s']});
    pause(0.0001);
end

3.3 参考资料

[1]张涵信.无波动、无自由参数的耗散差分格式[J].空气动力学学报,1988(02):143-165.

[2]周建忠,沈伟,杜杨.基于Steger-Warming矢通分裂的差分算法[J].重庆工业高等专科学校学报,2003(01):17-19.

[3]吴颂平,刘赵淼.计算流体流体力学基础及其应用[M].北京:机械工业出版社,2007,6.

[4]有限差分法求解Sod激波管问题 - 百度文库 (baidu.com)

qq_45885422

关注

30
点赞
踩
81

收藏

觉得还不错? 一键收藏
11
评论
求解一维Sod激波管问题

本文是计算流体力学课程的大作业项目，全文基于Matlab代码编写，希望能够给相关专业的同学提供一些帮助。在查找资料时，发现网上已有很多现成可用的代码，而我在本科时接触的比较多的也是CFD，想特别一些，因此在查论文时，发现了一些可用的方法，相当于复刻论文了。本文基于张涵信院士提出的NND计算格式，采用Steger_Warming矢通量分裂方法。张涵信院士是我国计算流体力学开创者和奠基人之一，长期致力于结合物理分析的计算流体力学理论和应用研究，为我国航空航天事业作出突出贡献。...
复制链接

扫一扫