递归的方式

递归的方式实现取数组最大值

    @Test
    public void TestMax() {
        int a[] = {0, 1, 2, 5, 3, 2, 1, 8, 4, 2, 0};
        System.out.println(getMax(a));
    }

    public int getMax(int[] arr) {
        return recursion(arr, 0, arr.length - 1);
    }

    //arr[l...r]范围上求最大值
    public int recursion(int[] arr, int l, int r) {
        if (l == r) {     //arr[l...r]范围上只有一个数，直接返回
            return arr[l];
        }
        int mid = l + ((r - l) >> 1); //求中点，防止溢出
        int leftMax = recursion(arr, l, mid);
        int rightMax = recursion(arr, mid + 1, r);
        return Math.max(leftMax, rightMax);
    }

归并排序

• 其用到的核心思想分治

先局部排序，，，，，，然后整体排序

先把一个完整的数组分为两半（左一半，右一半，然后再把左边分成两半，，，，，直到不能再分，然后排序，，，，左边排，右边排。。。）最后整体排序

空间换时间
时间复杂度O(nlogn)

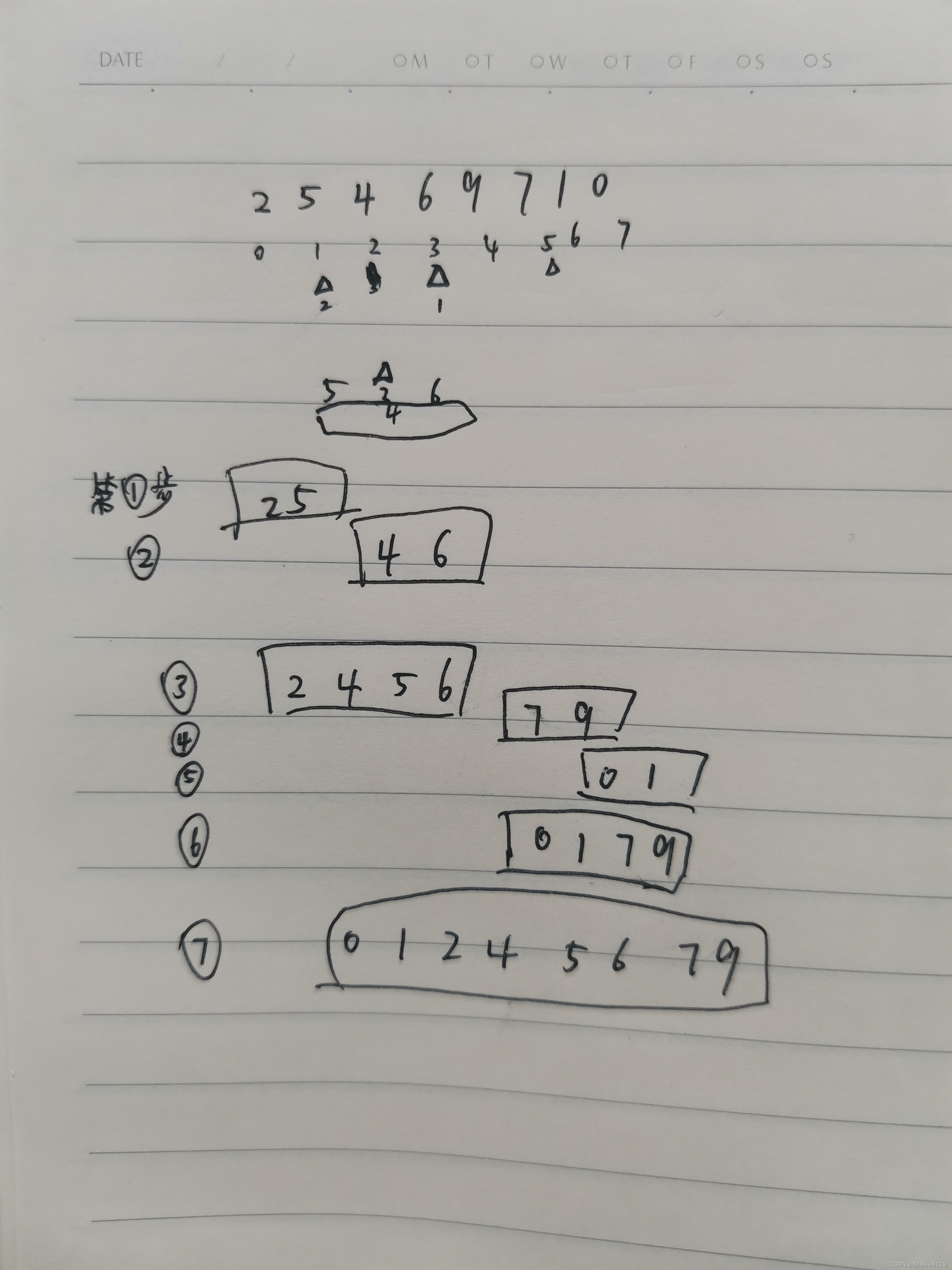
 @Test
    public void sort(){
        int a[]={2,5,4,6,9,7,1,0};
        process(a,5,7);
        for (int i = 0; i < 8; i++) {
            System.out.print(a[i]);
        }
    }

    /**
     * 递归，二分排序
     * @param arr
     * @param l
     * @param r
     */
    public void process(int[] arr, int l, int r) {
        if (l == r) {
            return;
        }
        int mid = l + ((r - l) >> 1);
        process(arr, l, mid);   //左边有序
        process(arr, mid + 1, r);   //右边有序
        merge(arr, l, mid, r);
    }

    /***
     * 排序
     * @param arr
     * @param l
     * @param mid
     * @param r
     */
    private void merge(int[] arr, int l, int mid, int r) {
        int[] help = new int[r - l + 1];   //把局部排好序的数组存放进来
        int i = 0;  //用于新数组的索引
        int j = l;
        int k = mid + 1;
        while (j <= mid && k <= r) {
            help[i++] = arr[j] <= arr[k] ? arr[j++] : arr[k++];
        }
        while (j<=mid){
            help[i++] = arr[j++];
        }
        while (k<=r){
            help[i++] = arr[k++];
        }

        /**
         * 把排好序的新数组赋给老数组
         */
        for (i = 0; i < help.length; i++) {
            arr[l+i] = help[i];
        }
    }

归并排序的扩展