LeetCode 剑指 Offer II 堆专题总结

最新推荐文章于 2022-06-19 19:26:02 发布

一只小逸白

最新推荐文章于 2022-06-19 19:26:02 发布

阅读量1.2k

点赞数 18

分类专栏： LeetCode 文章标签： leetcode 算法堆排序 map

本文链接：https://blog.csdn.net/qq_45911678/article/details/122554755

版权

LeetCode 专栏收录该内容

25 篇文章 1 订阅

订阅专栏

📚 博客主页：⭐️这是一只小逸白的博客鸭~⭐️
👉 欢迎关注❤️点赞👍收藏⭐️评论📝
😜 小逸白正在备战实习，经常更新面试题和LeetCode题解，欢迎志同道合的朋友互相交流~
💙 若有问题请指正，记得关注哦，感谢~

往期文章：

059. 数据流的第 K 大数值

题目：

设计一个找到数据流中第 k 大元素的类（class）。注意是排序后的第 k 大元素，不是第 k 个不同的元素。
请实现 KthLargest 类：

KthLargest(int k, int[] nums) 使用整数 k 和整数流 nums 初始化对象。
int add(int val) 将 val 插入数据流 nums 后，返回当前数据流中第 k 大的元素。

示例：

输入：
[“KthLargest”, “add”, “add”, “add”, “add”, “add”]
[[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]]
输出：
[null, 4, 5, 5, 8, 8]
解释：
KthLargest kthLargest = new KthLargest(3, [4, 5, 8, 2]);
kthLargest.add(3); // return 4
kthLargest.add(5); // return 5
kthLargest.add(10); // return 5
kthLargest.add(9); // return 8
kthLargest.add(4); // return 8

提示：

1 <= k <= 104
0 <= nums.length <= 104
-104 <= nums[i] <= 104
-104 <= val <= 104
最多调用 add 方法 104 次
题目数据保证，在查找第 k 大元素时，数组中至少有 k 个元素

思路：

创建一个小顶堆，将所有元素过一遍，剩下的 k个元素，堆顶就是 第 K 大数值
KthLargest(int k, vector<int>& nums)：初始化时 nums数组不一定大于 k个元素，有可能k-1，当add()后刚好是k个
遍历数组，将所有元素加入堆中，通过 add() 入堆
add() ：直接入堆，如果长度大于k，就将堆顶弹出

class KthLargest {
public:
    priority_queue<int, vector<int>, greater<int> > pq;
    int k;
    KthLargest(int k, vector<int>& nums) {
        this->k = k;
        for(auto& i : nums) {
            //直接调用add方法
            add(i);
            // 先入堆，然后再出就不用调用add
            //pq.push(i);
        }
        //while(pq.size() > k) pq.pop();
    }
    
    int add(int val) {
        pq.push(val);
        if(pq.size() > k) pq.pop();
        return pq.top();
    }
};

060. 出现频率最高的 k 个数字

题目：

给定一个整数数组 nums 和一个整数 k ，请返回其中出现频率前 k 高的元素。可以按 任意顺序 返回答案。

示例：

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

提示：

1 <= nums.length <= 105
k 的取值范围是 [1, 数组中不相同的元素的个数]
题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的
进阶：所设计算法的时间复杂度必须优于 O(n log n) ，其中 n 是数组大小。

思路：

可以用小顶堆pair<int,int>,（数字，出现次数）求解，自定义排序方法，以数字出现次数比较大小

用map统计数字出现次数
遍历map 将[key,val] 加入堆中，如果超过 k个元素就出堆，维护堆中只能有k个元素

class Solution {
public:
    // 自定义排序，按照出现次数排序
    static bool cmp(pair<int, int>& m, pair<int, int>& n) {
        return m.second > n.second;
    }
    vector<int> topKFrequent(vector<int>& nums, int k) {
        /*
        // 也可以这样使用lambda 定义， &cmp 有无引用符号的区别
        auto cmp = [](pair<int, int>& m, pair<int, int>& n) {
            return m.second > n.second;
        };
       priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> pq(cmp);*/
       
       // 小顶堆
       priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(&cmp)> pq(cmp);
       // 两种插入方法:
       // 1. pq.emplace(key,val); 
       // 2. pq.push(pair(key,value));
       unordered_map<int, int> map;
       for(auto& i : nums) {
           map[i]++;
       }
       for(auto& [key, value] : map) {
           pq.emplace(key,value);
           if(pq.size() > k) pq.pop();
       }
       vector<int> res;
       while(!pq.empty()) {
           res.push_back(pq.top().first);
           pq.pop();
       }
       return res;
    }
};

061. 和最小的 k 个数对

题目：

给定两个以升序排列的整数数组 nums1 和 nums2 , 以及一个整数 k 。
定义一对值 (u,v)，其中第一个元素来自 nums1，第二个元素来自 nums2 。
请找到和最小的 k 个数对 (u1,v1), (u2,v2) ... (uk,vk) 。

示例：

输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释: 返回序列中的前 3 对数：
[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]

提示:

1 <= nums1.length, nums2.length <= 104
-109 <= nums1[i], nums2[i] <= 109
nums1, nums2 均为升序排列
1 <= k <= 1000

思路：

将nums1可能的答案入堆，对应nums2的首元素下标为 0，[index1,0]配对入堆
而后面一取一个最小值[index1, index2]，就将 index2 的右边元素配对index1加入堆，这样可以保证堆里元素都是目前最小的
如下图：此时堆中初始化有三个元素，{[0,0],[1,0], [2,0] }

此时[0,0]最小，出堆后再将[0,1]入堆
此时[0,1]最小，出堆后再将[0,2]入堆
堆中元素为：{[0,2],[1,0], [2,0] }，不断重复k此就可得到答案

class Solution {
public:
    vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
        // 小顶堆，存下标，比较的时候用数组比较
        // 要引用 nums1, nums2，所以不能像上一题一样在类外定义
        auto cmp = [&](pair<int, int>& m, pair<int, int>& n) {
            return num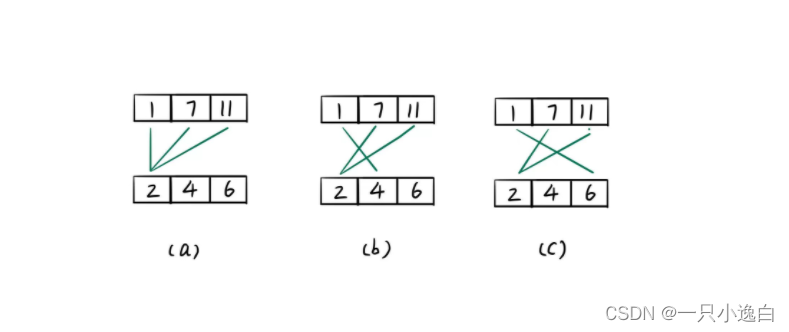![请添加图片描述](https://img-blog.csdnimg.cn/4898a8aa15804025b5893ed4b9a82311.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5LiA5Y-q5bCP6YC455m9,size_20,color_FFFFFF,t_70,g_se,x_16)
s1[m.first] + nums2[m.second] > nums1[n.first] + nums2[n.second];
        };
        // 小顶堆，如果在类外 static定义cmp的话，decltype(&cmp)，要加引用符号&
        priority_queue<pair<int, int>, vector<pair<int, int> >, decltype(cmp)> pq(cmp);
        vector<vector<int>> res;
        int n = nums1.size();
        int m = nums2.size();
        // 将nums1可能的答案入堆，后面只移动nums2的元素就可以了
        for(int i = 0; i < min(n, k); i++) {
            // nums1 可能是答案的只有 前 min(n, k) 个
            pq.emplace(i,0);
            //pq.push(pair<i,0>);
        }
        while(k-- && !pq.empty()) {
            auto top = pq.top();
            pq.pop();
            // 直接加入二维数组
            res.push_back({nums1[top.first], nums2[top.second]});
            // nums2 数组下标不越界就加入堆
            if(top.second + 1 < m) {
                pq.emplace(top.first, top.second + 1);
            }
        }
        return res;
    }
};

378. 有序矩阵中第 K 小的元素（此题与第三题类似）

题目：

给你一个 n x n 矩阵 matrix ，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。
请注意，它是排序后的第 k 小元素，而不是第 k 个不同的元素。

示例：

输入：matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
输出：13
解释：矩阵中的元素为 [1,5,9,10,11,12,13,13,15]，第 8 小元素是 13

提示：

n == matrix.length
n == matrix[i].length
1 <= n <= 300
-109 <= matrix[i][j] <= 109
题目数据保证 matrix 中的所有行和列都按非递减顺序排列
1 <= k <= n2

思路：

还是小顶堆，比较的是二维数组的值，存储数组的行列下标pair<int,int>(行，列)
构图一下，这就是初始化一列，然后按行扫到行尾，堆大小 <= 行数

将每一行的行首入堆[row,0]，遍历前k-1个元素，
遍历当前元素时，代表当前元素是当前所有行中最小的，出堆后将右边元素入堆
剩下的堆中，堆顶就是第k小的元素

class Solution {
public:
    int kthSmallest(vector<vector<int>>& matrix, int k) {
        // 思路： 先存入第一列，然后每取一个数（出堆）后就加入这个数的右边数（入堆）
        auto cmp = [&](pair<int, int>& m, pair<int, int>& n) {
            return matrix[m.first][m.second] > matrix[n.first][n.second];
        };
        // 小顶堆
        priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> pq(cmp);
        int n = matrix.size();
        int m = matrix[0].size();
        // 添加每一行的行首
        for(int i = 0; i < n; i++) {
            pq.emplace(i, 0);
        }
        //遍历前 k-1 个
        for(int i = 0; i < k-1; i++) {
            auto top = pq.top();
            pq.pop();
            // second的下一个下标是否数组越界
            if(top.second + 1 < m) {
                pq.emplace(top.first, top.second + 1);
            }
        }
        // 返回第 K 个
        return matrix[pq.top().first][pq.top().second];
    }
};