B. Phoenix and Puzzle（思维）

使用直角等腰三角形拼正方形的算法解析

最新推荐文章于 2021-05-06 19:42:51 发布

原创最新推荐文章于 2021-05-06 19:42:51 发布 · 430 阅读

2 ·

CC 4.0 BY-SA版权

思维专栏收录该内容

11 篇文章

订阅专栏

这篇博客讨论了一种数学问题，即如何用给定数量的相同直角等腰三角形拼成一个正方形。通过分析样例，指出当小正方形个数为完全平方数时，可以实现拼接。文章提供了C++代码实现，检查输入的三角形数量是否能组成正方形，并给出了样例测试的解决方案。

time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
Phoenix is playing with a new puzzle, which consists of n identical puzzle pieces. Each puzzle piece is a right isosceles triangle as shown below.
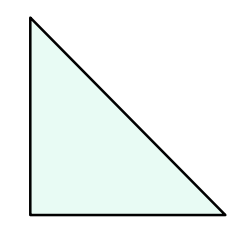
在这里插入图片描述

A puzzle piece
The goal of the puzzle is to create a square using the n pieces. He is allowed to rotate and move the pieces around, but none of them can overlap and all n pieces must be used (of course, the square shouldn’t contain any holes as well). Can he do it?

Input
The input consists of multiple test cases. The first line contains an integer t (1≤t≤104) — the number of test cases.

The first line of each test case contains an integer n (1≤n≤109) — the number of puzzle pieces.

Output
For each test case, if Phoenix can create a square with the n puzzle pieces, print YES. Otherwise, print NO.

Example
inputCopy
3
2
4
6
outputCopy
YES
YES
NO
Note
For n=2, Phoenix can create a square like this:

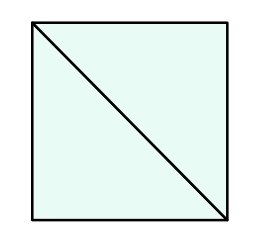
在这里插入图片描述

For n=4, Phoenix can create a square like this:
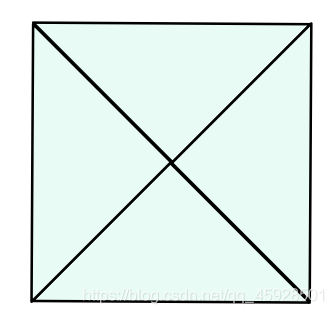
在这里插入图片描述

For n=6, it is impossible for Phoenix to create a square.

分析：

题意是有n个相同的直角等腰三角形，要求恰好用这n个直角三角形组成一个正方形。其实由样例可以看出1个小正方形最少可以由2个或4个直角三角形组成，而大正方形由x*x个小正方形组成，x是大正方形的边长，所以只要判断小正方形的个数是不是完全平方数即可。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1<<21;
int a[110];
int main()
{
	int T;
	scanf("%d",&T);
	while(T--)
	{
		int n,x;
		scanf("%d",&n);
		if(n%2==0)
		{
			x=n/2;
			int t=sqrt(x);
			if(t*t==x) 
			{
				printf("YES\n");
				continue;
			}
		}
		if(n%4==0)
		{
			x=n/4;
			int t=sqrt(x);
			if(t*t==x) 
			{
				printf("YES\n");
				continue;
			}
		}
		printf("NO\n");
	}
	return 0;
}