KMP算法介绍

数据结构中串的匹配算法–KMP算法笔记

你好！很高兴你能检阅到本文，感谢花时间阅览，为方便学习，该文是本人对KMP算法的粗略学习笔记，如有不足，烦请你给予指正。

前言

在我们使用字符串的时候，常会遇到字符串的模式匹配问题。这是一种常用的运算，所谓模式匹配,可以简单地理解为在目标(字符串)中寻找一个给定的模式(也是字符串)，返回目标和模式匹配的第一个子串的首字符位置。通常目标串比较大，而模式串则比较短小（目标串和模式串也即主串和子串）。遗憾的是许多字符串的模式匹配问题效率都不太高，比如朴素的模式匹配算法（BF算法）。为了进一步改进，D.E.Knuth，J.H.Morris和V.R.Pratt提出了KMP算法，即克努特—莫里斯—普拉特操作（简称KMP算法）。此算法主要消除了主串指针的回溯，使得算法效率有了一定程度的提高。

BF算法简介

BF算法，即暴力(Brute Force)算法的简称，是普通（朴素）的模式匹配算法，BF算法的思想就是将目标串（主串）S的每个个字符依次与模式串（子串）T的字符进行匹配，即将目标串S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和 T的第二个字符；若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果。
该算法采用穷举法的思路，最好情况下只需比较子串的长度值次，最坏情况下要进行M*(N-M+1)次比较，时间复杂度为O(M*N)。
1、如王卓老师课堂上的这个例子：
对于两个字符串，我们按顺序将其存放在数组中，鉴于数据下标从0开始，为方便起见，0位置不存放字符，而是从1开始，即初始化

i = 1 ； j = 1 ；

字符串从第一个字符开始依次进行匹配，若第一个匹配成功，则 i++，j++，当 i，j = 4 时， 发现

 S.ch[i] !=  T.ch[j] ;

此时 i 回溯到第二个字符，j 回退到 1 位置 ，即 i = 2 ，j = 1 从新开始，用 i = 2,3,4,5四个字符继续依次与 j 对应字符匹配。 可知，若匹配失败，则按 i = i - j + 1 +1 进行回溯，j = 1 从头开始。（其中 i - j 表示移动的格数 ，i - j + 1 表示退回到原来位置，i - j + 1+ 1 则表示退回到原来位置的下个位置），匹配成功时，i = 7，j = 5 ，return i - t.length = 3.。得到匹配成功时 i 的位置。
2、BF算法描述

int Index_BF(SString S, SString T){//如果需要从某个位置开始比较，则可增加参数 pos，即int Index_BF(SString S, SString T ，int pos)
  	  int i = 1, j = 1 ;           // 此时 i = pos ; 其他不变
  	  while(i < S.length && j < T.length){
  		  if (S.ch[i] == T.ch[j]){
  		  			i ++;
  		  			j ++;
  		  }
  		  else { i = i - j + 2 ; j = 1 ;}
  	 }
		if(j >= T.length) return i - T.length;
		else  return  0 ;
}

KMP算法

与BF算法相比，KMP算法的主串指针 i 是不需要回溯的，这样时间复杂度可以提高到O(n+m)，而且 j 也不一定要从头开始，从而使该算法得到某种程度的提高。

字符串名称	字符串内容	数据下标	长度（为方便观察，特意给字符串加了空格，实际长度应为字符个数）
S(主串)	‘ a b a b c a b c a c b a b ’	i	13
T(子串)	‘ a b c a c ’	j	5

同样，以 S 为主串，以 T 为子串对KMP算法的思路进行说明。我们发现，当 i = 3，j = 3 时， S.ch[i] != T.ch[j] ，此时按BF算法，j 从头开始， i 回溯，但对于KMP算法而言，i 不需要回溯了，在哪不匹配成功的，从哪开始，即此时 i 从 i = 3 位置开始匹配，同时 j 有的时候也不需要从头开始，如当 i = 7，j = 5 时，匹配不成功，此时 i 从 i = 7开始，而由于子串T中的第一个字符 a 与 j=4 对应的 字符a相等，且前面已经是匹配成功了的，这种情况下，j 从 j = 2 开始即可。（图解如下）

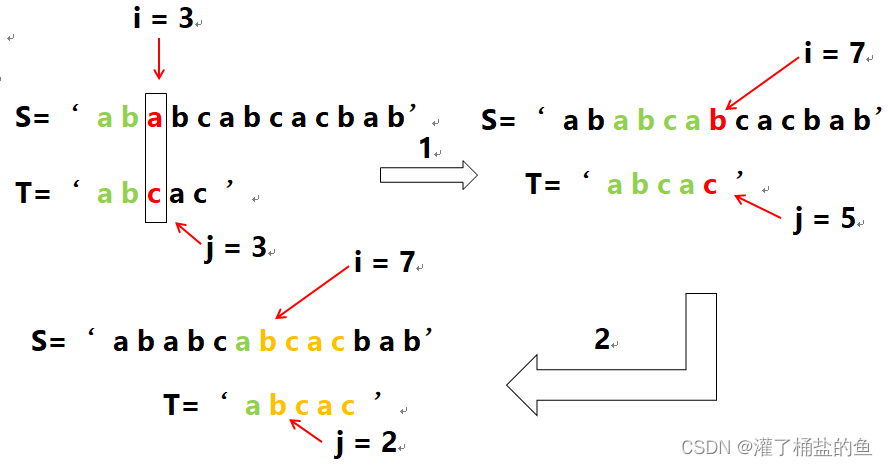
由上可知 i 的位置比较容易定位，但是 j何时才不需要从头开始？且看如下官方数学公式吧。

官方定义了 next[j] 数组，表明当子串中第 j 个字符与主串中相应字符“失配”时，在子串中需重新和主串中该字符进行比较的字符的位置，且next数组的数值只与子串本身有关。
说人话就是，当 j 为 1 时，next[j] = 0 ,当该模式串（子串）集合非空时， next[j] 的值为前后缀相等的最长字符串的个数，即 k ，其他情况时 next[j] = 1。

所谓字符串前缀，就是给定一个字符串，有 k 个字符，将其视为一个集合，那么由第 k 个元素前的字符按顺序依次组成的集合就是这个字符串的前缀，后缀则相反。

例如：字符串 ‘abcde’ 的前缀是**{ ‘a’ ,‘ab’ , ‘abc’ ,‘abcd’ }, ‘abcde’ 不是，即它本身不是自己的前缀。
字符串 ‘abcde’ 的后缀是{ ‘e’ , ‘de’ ,‘cde’,‘bcde’ }, ‘abcde’ 不是，即它本身不是自己的后缀。
字符串 ‘abcdab’ 的前缀是{ ‘a’ , ‘ab’ ,‘abc’,‘abcd’,‘abcda’ }, ‘abcdab’ 不是，即它本身不是自己的前缀。
字符串 ‘abcdab’ 的后缀是{ ‘b’ , ‘ab’ ,‘dab’,‘cdab’,‘bcdab’ }**, ‘abcdab’ 不是，即它本身不是自己的后缀。
字符串 ‘abcdab’ 的最长相等先后缀就是 ‘ab’ ，此时 k = 3。

进一步深入理解，请仔细分析如下表格内容。

j	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
模式串	a	b	c	a	a	b	b	c	a	b	c	a	a	b	d	a	b
next[j] 值	0	1	1	1	2	2	3	1	1	2	3	4	5	6	7	1	2

KMP算法描述

int Index_KMP(SString S, SString T,int pos){
  	  int i = pos, j = 1 ;           
  	  while(i < S.length && j < T.length){
  		  if (j == 0 && S.ch[i] == T.ch[j]){
  		  			i ++;
  		  			j ++;
  		  }
  		  else { j = next[j] ;} // i 不变，j 后退。
       }
		if(j >= T.length) return i - T.length;
		else  return  0 ;
}

next[j] 的求法

int get_next(SString T,int &next[]){
  	  int i = 1, next[1] = 0; j = 0 ;           
  	  while( i < T.length ){
  		  if (j == 0 && T.ch[i] == T.ch[j]){
  		  			++ i;
  		  			++ j;
  		  			next[i] = j ;  //  next[i]=j,  含义是：下标为i 的字符串最长相等前后缀的长度为j。即用一个next数组存储子串的最长相等前后缀的长度
  		   }
  		  else  j = next[j] ;
        }
}

KMP算法中next函数的改进

鉴于在字符串匹配过程中，有时候会遇到一些特殊情况，导致时间复杂度的增加，此时，next 函数是可以进行优化的，如下面例子所示。
主串S=“aaabaaaab”
子串T=“aaaab”

由上发现，当 i = 4，j = 4 时匹配失败，此时 i 不动， 对比表中next[j]值对应4，所以j 回溯到 第3个位置，此时第3个位置的字符与主串同样失配，继续退，以此类推，直到 next[j] = 0, j = 1 ，此时 **i **移动一格，即 i=5，j=1，不难发现对于子串 T 第四个字符和前三个字符是一样的，没必要将前三个字符再次与主串中的第四字符比较，因为没必要让 j 往回退，直接 i 前进一步就行。 这时我们同样引入了一个数组 nextval[j] 。

j	1	2	3	4	5
模式串	a	a	a	a	b
next[j] 值	0	1	2	3	4

根据next 求 nextval的方法。（步骤参见王卓老师的内容）

模式串	a	b	a	a	b	c	a	c
next[j] 值	0	1	1	2	2	3	1	2
nextval[j] 值	0	1	0	2	1	3	0	2

KMP算法的时间复杂度
KMP算法其实就是通过消耗空间复杂度换尽可能少的时间复杂度。
我们知道求数组的过程其实是在消耗空间的，KMP算法就是利用这一点来实现空间换取时间的。当我们设主串S长度为n ,子串T 的长度为m时。求next[j] 数组时时间复杂度为O(m)，因其匹配过程中，主串不回溯，比较次数可记为n，所以KMP算法的总时间复杂度为O(m+n)，空间复杂度记为O(m)。相比于朴素的模式匹配（BF算法）时间复杂度O(m*n)，KMP算法提速是非常大的，通过消耗空间换得极高的时间提速是非常有意义的。