图论学习-差分约束入门

差分约束

一、什么是差分约束？

求不等式组的可行解。

1.1 概念

差分约束系统是一种特殊的N元一次不等式组，它包含N个变量X1~Xn,以及M个约束条件，每个约束条件都是由两个变量作差构成的，形如
$$\begin{gathered} X_i-X_j<=C_k(C_k是常数) \\ 注： \\ 必须是形如上式这样的形式 \\ 如果不是，需要转化成上式 \end{gathered}$$
需要解决的问题是：求一组解
$$X_1=a_1,X_2=a_2...使所有约束条件都能满足$$

1.2 与图论的联系

对于差分约束系统的每个约束条件$$X_i-X_j<=C_k$$都可以变形为$$X_i<=X_j+C_k$$

而它与最短路问题中的三角形不等式dist[y]<=dist[x]+z相似
所以可以把所有形如
$$X_i<=X_j+C_k$$
的式子看成是从 j 出发向 i 连一条长度为C_k的有向边
那么可以注意到：求解该不等式组的解就是对这个不等式所建的图求最短路径。

所以求差分约束的解的问题等价于求最短路的问题。

1.3 成立条件

对于求单源最短路问题，
源点需要满足条件：从源点出发，一定可以走到所有的边。需要找一个可以走到所有边的源点。

1.4 解题步骤

1. 先将每个不等式$$x_i<=x_j+c$$转化为一条从 j 走到 i ，长度为c的一条边
2. 找一个超级源点（或者建立一个虚拟源点），使得该源点一定可以遍历到所有边
3. 从源点求一遍单源最短路
   结果1：如果存在负环，则原不等式组一定无解，详见1.5
   结果2：如果没有负环，则dist[i]就是原不等式组的一个可行解。

1.5 特殊情况

如果图存在负环，比如下图的环是负环：

先观察图，易有：
$$\begin{gathered} x_2<=x_1+c_1......(1) \\ {x}_3<=x_2+c_2......(2) \\ ... \\ {x}_{k-1}<=x_{k-2}+c_{k-2}......(k-2) \\ {x}_k<=x_{k-1}+c_{k-1}......(k-1) \\ {x}_1<=x_k+c_k......(k) \end{gathered}$$
$$\begin{gathered} 观察易有x_2<=x_1+c_1<=x_k+c_k+c_1 \\ <=x_2+c_1+c_2+c_3+...+c_k \\ 而因为是负环，则c_1+c_2+c_3+...+c_k<0 \\ \therefore x2<=x2+(小于0的式子)显然矛盾 \\ \therefore 如果图中存在负环，那么不等式组一定存在矛盾，无解。 \end{gathered}$$

1.6 如何求最大值或者最小值

这里的最值指的是对于每个变量在满足约束条件情况下所能取得的最值。
结论：如果求的是最小值，则应该求最长路，如果求的是最大值，则应该求最短路。
问题1： 如何转化xi<=c？ 建立一个超级源点:0,然后建立0->i,长度为c的边即可。

二、例题

题目1：P3275 [SCOI2011]糖果

链接
分析：

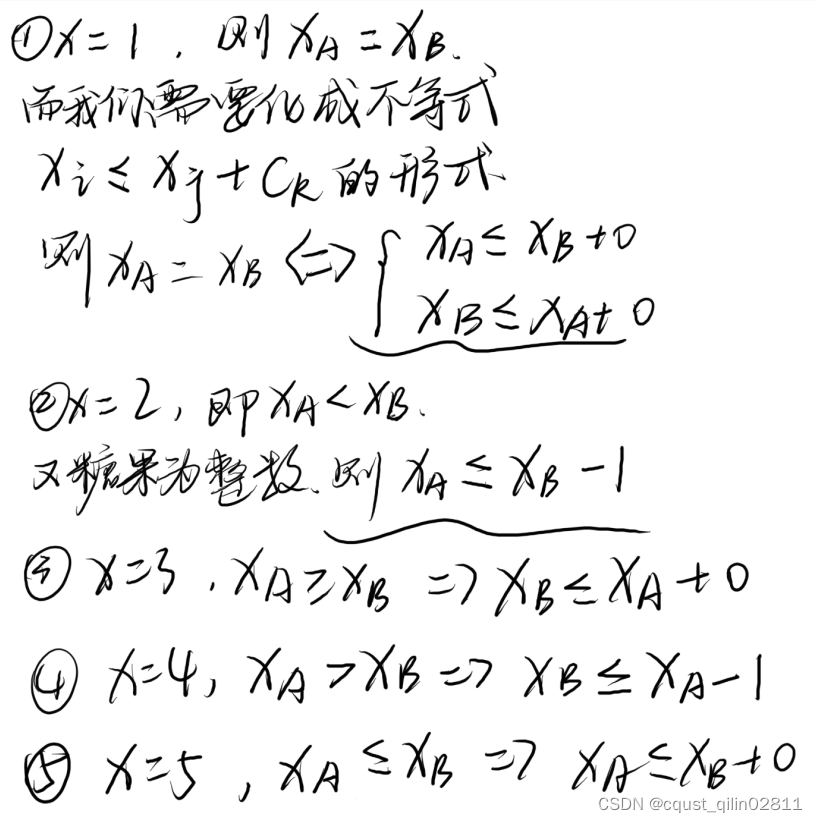
随后根据不等式建图，
ac code:

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const ll N = 2e6+10,M = N;
ll h[N], e[M], ne[M], w[M],idx;
ll dist[N],q[N],cnt[N];
bool st[N];
void add(ll a, ll b, ll c)  // 添加一条边a->b，边权为c
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
ll n,m;

bool spfa()
{
   memset(dist,-0x3f,sizeof dist);//因为是求最长路
   int hh = 0,tt = 1;
   dist[0] = 0;
   q[0] = 0;
   st[0] = true;
   while(hh<=tt)
   {
       auto t = q[--tt];
       st[t] = false;
       for(int i = h[t];~i;i = ne[i])
       {
           int j = e[i];
           if(dist[j]<dist[t]+w[i])
           {
               dist[j] = dist[t]+w[i];
               cnt[j] = cnt[t]+1;
               if(cnt[j]>=n+1) return false;
               if(!st[j])
               {
                   q[tt++] = j;
                   st[j] = true;
               }
           }
       }
   }
   return true;
}
int main()
{
    memset(h, -1, sizeof h);
    memset(st, 0, sizeof st);
    cin>>n>>m;
    while (m -- ){
        ll x,a,b;
        cin>>x>>a>>b;
        if (x == 1) add(b, a, 0), add(a, b, 0);//A=B
        else if (x == 2) add(a, b, 1);//B≥A+1
        else if (x == 3) add(b, a, 0);//A≥B
        else if (x == 4) add(b, a, 1);//A≥B+1
        else add(a, b, 0);
    }
    for(ll i = 1;i<=n;i++) add(0,i,1);
    bool t = spfa();
    if(!t)
    {
        cout<<"-1";
        return 0;
    }
    ll res = 0;
    for(ll i = 1;i<=n;i++)
    {
        res+=dist[i];
    }
    cout<<res;
    //求最小值，用最长路
    return 0;
}

后续更新~

题目2：