K-Means聚类
- 初始化:给定
k个随机初始化的中心点 - 迭代:计算每个簇当前的质心
- 计算每个点到点前簇中心的距离,并将他们分配进最近的簇
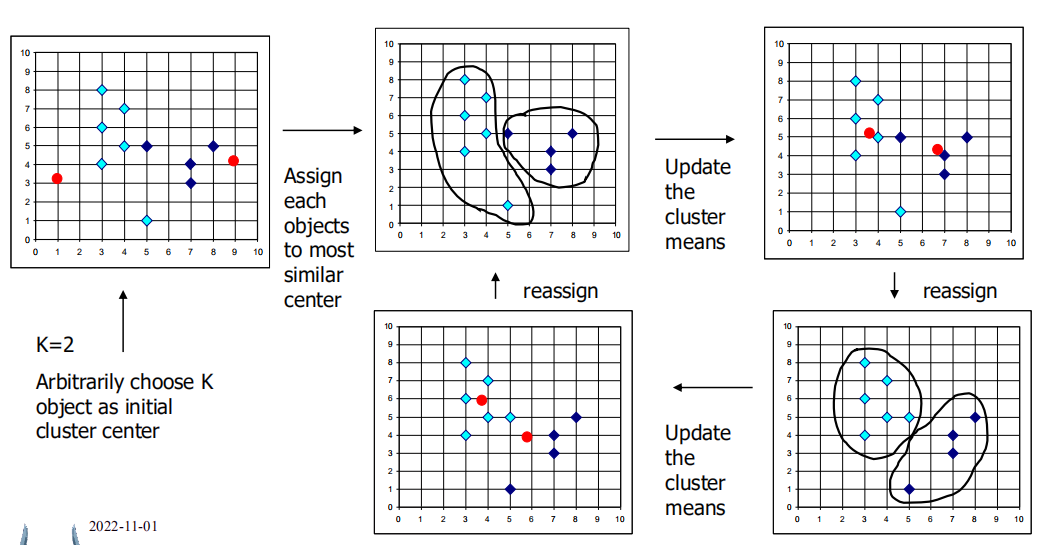
时间复杂度:O(tkn)O(tkn)O(tkn),nnn是对象个数,kkk是簇个数,ttt是迭代次数。
通常条件下会止于全局最优解。
缺点:
- 不适用于分类数据(只能计算数值)
- 需要指定聚类簇的个数
- 无法处理有噪声的情况和异常值
- 不适合发现非凸型的簇
变化
🏷 处理分类数据:k-modes算法
- 用模式(modes)代替原先的均值
- 基于新的不相似度量方式处理分类对象
- 使用一种基于频率的方式对簇进行更新
🏷 处理混合数据:k-prototype
🏷 期望最大化扩展
- 基于加权度量进行计算
🏷 处理异常数据:k-Medoids算法
- 采用簇中最中心的点来代替原先的均值,此时,这个中心点是实际存在的点
实现
import random
import math
# 随机生成100个点
points=[(random.randint(-50,50),random.randint(-50,50)) for i in range(100)]
def k_Means(poi,k=5,epochs=100):
# 初始化
centroid=[] # 质心点
cluster=[[0]*(len(poi[0]))+[0] for i in range(k)] # 记录一个簇中所有点每一个维度上坐标的总和,以及簇点的个数,这步是方便计算罢了
PoiClass=[-1 for i in range(len(poi))]# 映射表,输出每个点对应的类
Break=[-1 for i in range(len(poi))] # 用来控制逻辑,比如当这个表跟映射表的差距小于2时,我们就不迭代了
# 随机选取中心点
# 无放回抽样
for i in range(k):
if (v:=random.choice(poi)) not in centroid:
centroid.append(v)
# 计算每个点的欧氏距离
def edis(x,y):
return math.sqrt(sum([(x[i]-y[i])**2 for i in range(len(x))]))
# 开始迭代
for _ in range(epochs):
# 计算每个点到中心的距离
for pId,p in enumerate(poi):
dis,idx=2e31,0
for Idx,c in enumerate(centroid):
if (v:=edis(p,c))<dis:
dis,idx=v,Idx # 获取最小值时候的坐标
# 簇统计量,方便计算
for i in range(len(p)):
cluster[idx][i]+=p[i]
cluster[idx][-1]+=1 # 簇的数量
# 更新映射表
PoiClass[pId]=idx
# 重新计算每个簇的中心,这个中心是平均值,并不一定是存在的点
for i,v in enumerate(cluster):
new_c=[]
for j in range(len(v)-1):
new_c.append(v[j]/v[-1])
centroid[i]=new_c
cluster[i]=[0]*len(poi[0])+[0] # 将常量清零
# 设置终止迭代条件
if sum(PoiClass[i]==Break[i] for i in range(len(poi)))>=len(poi):
return PoiClass
Break=PoiClass[:]
return PoiClass







 本文详细介绍了K-Means聚类算法的原理,包括初始化、迭代过程以及时间复杂度分析。同时,讨论了算法的局限性,如对分类数据的不适用性、需要预设簇数量等。文章还提到了针对这些问题的改进算法,如k-modes、k-prototypes和k-Medoids。最后,给出了一个简单的K-Means聚类算法的Python实现示例。
本文详细介绍了K-Means聚类算法的原理,包括初始化、迭代过程以及时间复杂度分析。同时,讨论了算法的局限性,如对分类数据的不适用性、需要预设簇数量等。文章还提到了针对这些问题的改进算法,如k-modes、k-prototypes和k-Medoids。最后,给出了一个简单的K-Means聚类算法的Python实现示例。

















 822
822

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








