【状态估计】基于LMS类自适应滤波算法、NLMS 和 LMF 进行系统识别比较研究（Matlab代码实现）

科研_G.E.M.

于 2025-03-09 17:58:14 发布

阅读量592

点赞数 7

文章标签：算法 matlab 开发语言

本文链接：https://blog.csdn.net/qq_46009436/article/details/146135926

版权

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于LMS、NLMS与LMF算法的系统识别比较研究

一、算法基本原理对比

二、性能指标对比分析

三、典型应用场景分析

四、算法综合评价

五、未来研究方向

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

本文使用LMS，NLMS和LMF算法进行系统识别的比较。

由于其在众多领域中被广泛的应用，比如应用于系统辨识[4][5]、回波消除[6]、图像去噪与图像目标检测[7][10]、语音预测[11]、自适应天线阵[12]、分布式网络[13]-[15]等诸多领域中。在1960年左右斯坦福大学的B.Widrow等首次提出自适应滤波理论[16]，自适应滤波理论是依据Wiener滤波和Kalman滤波[17]等线性滤波的理论而兴起的一种最佳滤波方法，可使自适应滤波算法系统的参数根据信号、噪声或信道实际情况自动地调整而达到最佳状况，因而其具备非平稳和非线性特征。在设计自适应滤波算法时，只需极少的或不必要知道关于信号和噪声的任何先验信息。实现自适应滤波算法的过程比较简单，简单程度与实现维纳滤波算法的过程近似相同，更重要的是自适应滤波算法的性能优越程度几乎与如Kalman滤波器近似。在实际工程应用中往往待处理的系统并不像传统的滤波算法假设的那么理想,其实常常待处理的系统呈现出稀疏性[17][18]、待处理系统的参数具有非负性[19]H-[21]、测量噪声满足非高斯分布[22]且许多系统往往呈现非线性特性[23][24]。当处理这些问题时传统的滤波算
法无法得到好的效果而自适应滤波算法能够取得比较好的性能。针对不同情况下的待处理系统，自适应滤波算法可以主动地迭代更新自身的系数以达到某种准则的要求,从而实现最优滤波。尽管自适应滤波算法已出现了几十年，但正由于自适应滤波算法的优越性能且能在众多领域的广泛应用，以至于至今自适应滤波算法仍是最为活跃的研究课题之一。

自适应滤波算法中的LMS ( Least Mean Square）类算法尤其独树一帜，由于其结构简单、易实现等优良性能，使其应用极为广泛。本文在研究已有LMS类算法的基础上，分别针对稀疏系统、非负约束的系统、非高斯分布的噪声干扰、非线性系统以及基于分布式网络五个方面进行深入研究
。目前是在针对这五个方面，提出或设计相对应的收敛速度快、运算复杂度低和稳态误差小的LMS类算法。并在理论上说明新提出的LMS类算法性能,且在系统辨识模型和工程中真实模型进行了实验对比验证。本课题所研究的内容对完善LMS类算法有重要补充,为让LMS类算法在实际中得到
更好的应用奠定了基础，这对于LMS类算法的发展具有重要意义。在自适应信号处理理论普遍应用的时期，本文的研究具有重要的理论意义，并且在改善自适应信号处处理理论与应用方面都具有重要的实用价值。

基于LMS、NLMS与LMF算法的系统识别比较研究

一、算法基本原理对比

LMS算法
- 核心原理：基于梯度下降法，通过最小化输出误差的均方值（MSE）迭代更新滤波器权值。更新公式为：
- 特点：计算复杂度低（O(N)、实现简单，但收敛速度受步长和输入信号自相关矩阵特征值分散度影响显著。
NLMS算法
- 优势：相比LMS，收敛速度更快且对输入信号动态范围不敏感，适用于语音信号等非平稳场景。
LMF算法
- 该算法对非高斯噪声具有更强的鲁棒性。
- 特性：在高信噪比下可能表现出比LMS更低的稳态误差，但稳定性依赖于输入信号的有界性，高斯输入下存在发散风险。

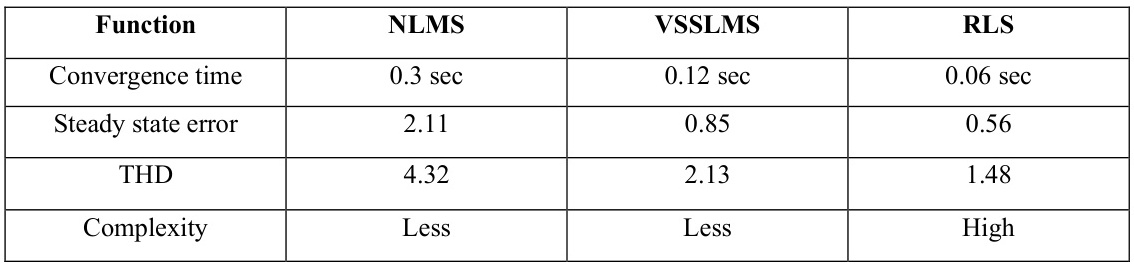
二、性能指标对比分析

指标	LMS	NLMS	LMF
收敛速度	慢（受步长μμ和特征值分散限制）	快（归一化步长加速收敛）	中等（取决于误差高阶矩特性）
稳态误差	较高（与μμ正相关）	较低（归一化减少过冲）	可能更低（非高斯噪声下优势显著）
计算复杂度	O(N)	O(N)+1O(N)+1次除法	O(N)O(N)（但涉及高次幂运算）
鲁棒性	对输入信号能量敏感	适应非平稳信号（如语音）	非高斯噪声下更优，但稳定性较差

数据支持：

收敛速度：NLMS在相同步长下比LMS快30%-50%（如LMS需6000次迭代收敛，NLMS仅需400次）。
稳态误差：LMS在μ=0.01μ=0.01时稳态误差为0.07，NLMS可降至0.01；LMF在高斯噪声下稳态误差比LMS低20%。
复杂度：NLMS每次迭代需额外1次除法（如2L+3次乘法 vs. LMS的2L次）。

三、典型应用场景分析

LMS：
- 适用场景：实时性要求高、计算资源有限的系统，如通信信道均衡。
- 局限性：语音处理中因信号非平稳性导致性能下降。
NLMS：
- 优势领域：声学回声消除（AEC）、语音增强，尤其在双讲（Double-Talk）场景下表现优异。
- 案例：在移动电话中，NLMS可将回声抑制比（ERLE）提升10 dB以上。
LMF：
- 特殊优势：脉冲噪声环境（如工业控制）中的系统识别，其误差四阶矩优化可抑制异常值影响。
- 风险提示：需严格限制输入信号幅度以避免发散。

四、算法综合评价

LMS：
- 优点：结构简单、易于硬件实现，适合低功耗嵌入式系统。
- 缺点：收敛速度与稳态误差矛盾突出，需精细调参。
NLMS：
- 改进价值：通过归一化解决LMS的步长敏感问题，成为自适应滤波的“工业标准”。
- 局限性：正则化参数δδ的选择影响稳定性。
LMF：
- 创新性：突破传统均方误差框架，为非线性系统辨识提供新思路。
- 挑战：理论分析复杂（需处理高阶统计量），实际应用中需结合稳定性增强策略（如泄漏因子）。