💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
【VMD分解】包含包络线,包络谱,中心频率,峭度值,能量熵,样本熵,模糊熵,排列熵,近似熵,包络熵,频谱图研究
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能解答你胸中升起的一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
基于170余种智能算法优化的VMD方法及其多指标可视化研究
一、VMD基本原理与参数优化需求
变分模态分解(Variational Mode Decomposition, VMD)是一种自适应信号分解方法,通过构造变分问题将输入信号分解为多个准正交的固有模态函数(IMF),每个IMF具有中心频率和有限带宽特性(Ev1)。其核心参数包括:
- 模态数K:决定分解的IMF数量;
- 惩罚因子α:控制IMF的带宽和抗噪能力(Ev2)。
传统VMD需手动设置参数,而实际应用中参数的敏感性会导致分解结果差异显著。例如,K值过小导致模态混叠,过大则引入冗余分量;α值过低会扩大带宽,过高则抑制噪声能力下降(Ev8)。因此,引入智能算法进行参数优化成为必要。
二、170余种智能算法的分类与特点
根据文献分类,用于优化VMD的智能算法可分为以下类别:
| 算法类型 | 代表算法 | 优化特点 |
|---|---|---|
| 群体智能算法 | 粒子群优化(PSO)、遗传算法(GA)、灰狼优化(GWO)、麻雀算法(SSA) | 全局搜索能力强,适用于高维参数空间,需平衡探索与开发能力(Ev10) |
| 仿生学算法 | 黏菌算法(SMA)、海洋捕食者算法(MPA)、鲸鱼优化算法(WOA) | 模仿生物行为,具有动态调整搜索策略的优势(Ev14) |
| 物理启发算法 | 霜冰算法(RIME)、多元宇宙算法(MVO) | 基于物理现象(如热传导、引力作用),参数少且收敛速度快(Ev19) |
| 混合改进算法 | IDBO(改进的麻雀算法)、HHO(哈里斯鹰算法) | 结合混沌映射、Levy飞行等机制,避免局部最优(Ev15) |
| 深度学习优化器 | 堆叠稀疏自编码器(SSAE)与智能算法结合 | 适用于复杂时序特征提取,需结合模态分量能量熵等指标(Ev10) |
优化流程(以PSO为例):
- 初始化:设置参数范围(如α∈[100,2500],K∈[3,10])(Ev42)。
- 适应度计算:通过VMD分解信号,计算目标函数值(如包络熵)。
- 迭代更新:根据粒子位置和速度更新参数组合。
- 收敛判定:达到最大迭代次数或适应度阈值时终止。
三、五种适应度函数的形式与切换机制
适应度函数用于量化VMD分解效果,常见形式及数学定义如下:

【VMD分解】包含包络线,包络谱,中心频率,峭度值,能量熵,样本熵,模糊熵,排列熵,近似熵,包络熵,频谱图研究
一、VMD分解基本原理与流程
1. 核心思想与数学模型
VMD(Variational Mode Decomposition)是一种基于变分贝叶斯理论的非递归信号分解方法,旨在将复杂信号分解为多个有限带宽的模态分量(IMF)。其数学本质是求解约束变分问题,最小化所有模态带宽之和。目标函数表示为:

2. 分解流程
- 初始化参数:设定模态数KK、惩罚因子αα(控制带宽)和收敛容差。
- 迭代优化:通过交替方向乘子法(ADMM)更新模态分量和中心频率:
- 模态更新:利用维纳滤波在频域分离信号;
- 中心频率更新:计算模态分量的频谱质心。
- 收敛判定:当模态更新量小于容差或达到最大迭代次数时终止。
3. 参数选择的影响
- 模态数KK:过小导致欠分解,过大会出现中心频率相近的冗余模态(如中K=4K=4时出现重叠,需调整至K=3K=3)。
- 惩罚因子αα:值越大,模态带宽越小,频率分辨率越高,但可能丢失高频细节。
二、包络线与包络谱分析
1. 包络线计算
通过希尔伯特变换提取信号的高频振荡包络:

其中H为希尔伯特变换算子。
2. 包络谱生成
对包络信号进行FFT得到频谱,用于识别调制频率(如轴承故障特征频率fBPFOfBPFO)。优势在于抑制载频干扰,突出故障冲击成分。
应用案例:在轴承外圈故障诊断中,包络谱在fBPFOfBPFO处呈现显著峰值,而原始频谱可能被噪声淹没。
三、中心频率的提取与判定
1. 中心频率定义
每个IMF的中心频率ωkωk代表其能量集中区域的频域位置,通过迭代优化确定。
2. 判定方法
- 斜率法:比较模态中心频率的斜率与瞬时平均频率,若不一致则停止分解。
- 重叠准则:当相邻模态中心频率差值小于阈值时,判定为过分解(如中K=4时4038 Hz与4498 Hz相近,需减少K)。
四、峭度值在故障诊断中的应用
1. 计算公式
峭度(Kurtosis)衡量信号分布的尖峰特性:
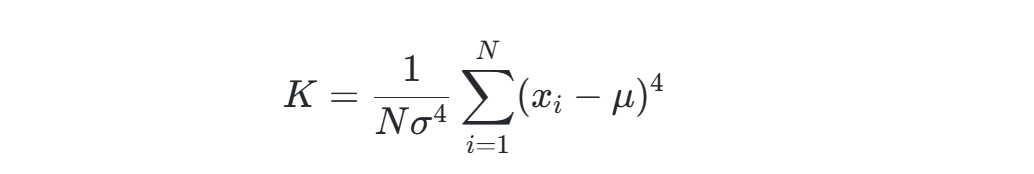
其中μ为均值,σ为标准差。
2. 诊断意义
- 正常状态:峭度值接近3(正态分布);
- 故障状态:峭度值显著增大(如K>8K>8提示严重冲击性故障)。
应用场景:滚动轴承早期表面损伤时,峭度对微弱冲击敏感,优于传统RMS指标。
五、熵特征分析
1. 各类熵的定义与区别
| 熵类型 | 数学定义 | 特点与应用 |
|---|---|---|
| 能量熵 | Ee=−∑pilnpi, pi=Ei/∑Ei | 反映能量分布复杂度,适用于模态分量能量分布分析 |
| 样本熵 | 基于相空间相似性,排除自匹配统计量 | 改进近似熵,抗噪性强,用于生理信号与机械振动分析 |
| 模糊熵 | 引入指数隶属函数e−dijn/re−dijn/r替代阶跃函数 | 处理模糊边界问题,对阈值rr变化更鲁棒 |
| 排列熵 | 基于序列符号化排列模式的概率计算 | 计算高效,适用于在线监测,擅长检测动力学突变 |
| 近似熵 | ApEn=lnCm(r)Cm+1(r) | 早期方法,依赖数据长度,易受噪声影响 |
| 包络熵 | 对包络信号计算样本熵或模糊熵 | 结合包络解调与熵分析,增强故障特征提取 |
2. 应用实例
- 故障分量筛选:计算各IMF的峭度值与包络熵,选择熵值最小(或峭度最大)的模态进行后续分析。
- 健康状态评估:利用多尺度熵量化信号复杂度变化,如齿轮磨损导致熵值降低。
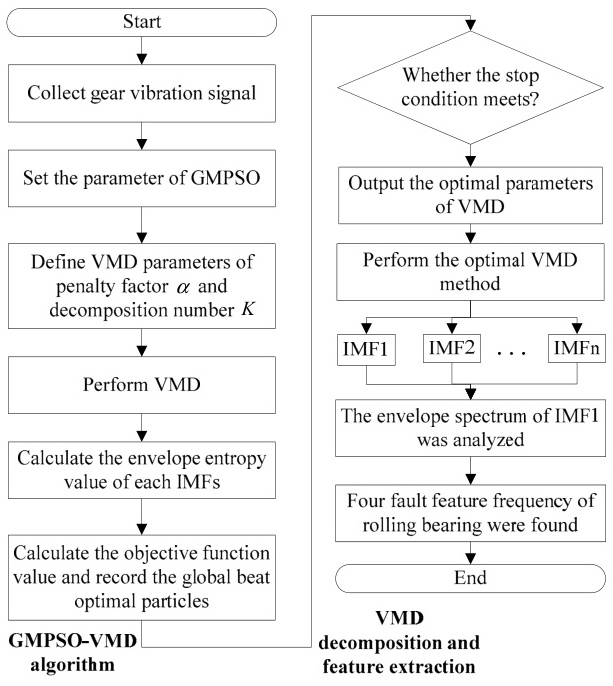
六、频谱图生成方法
1. 步骤
- VMD分解:获取各IMF分量uk(t)uk(t);
- FFT变换:对每个uk(t)uk(t)进行快速傅里叶变换,得到频谱Uk(f)Uk(f);
- 可视化:绘制各IMF的时域波形与频谱图,标注中心频率(如图右侧子图)。
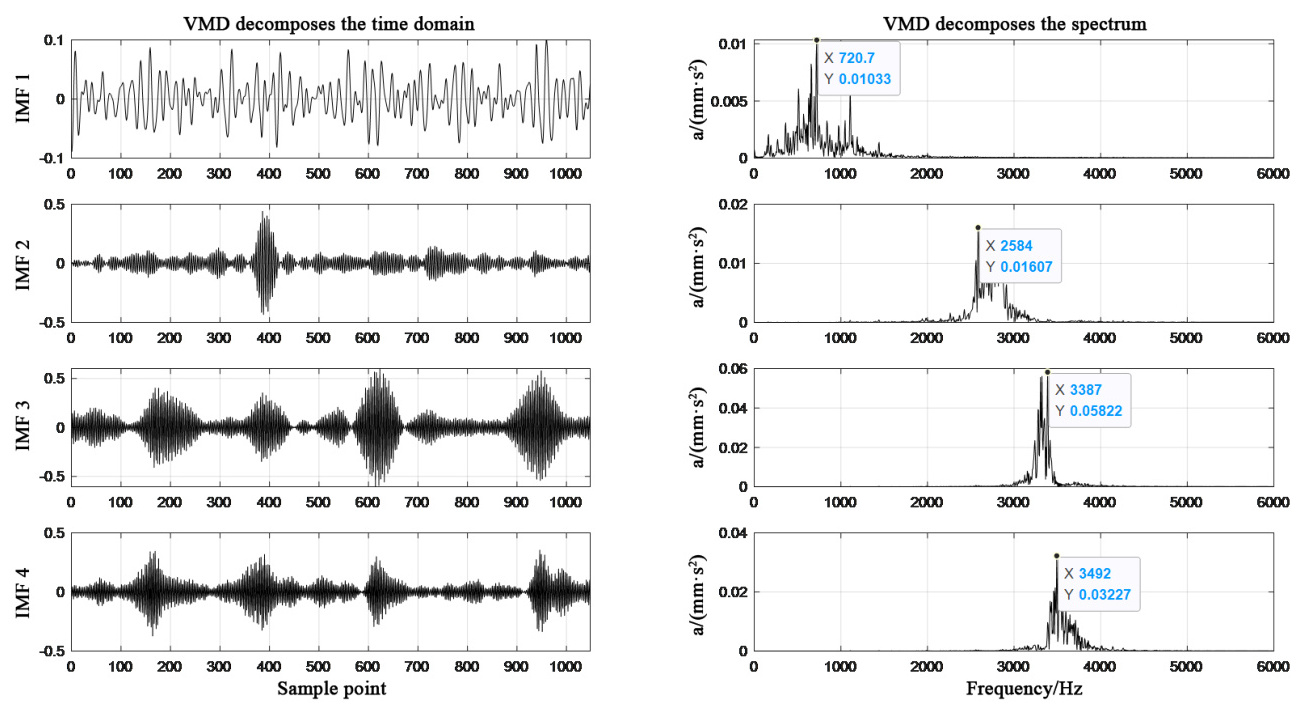
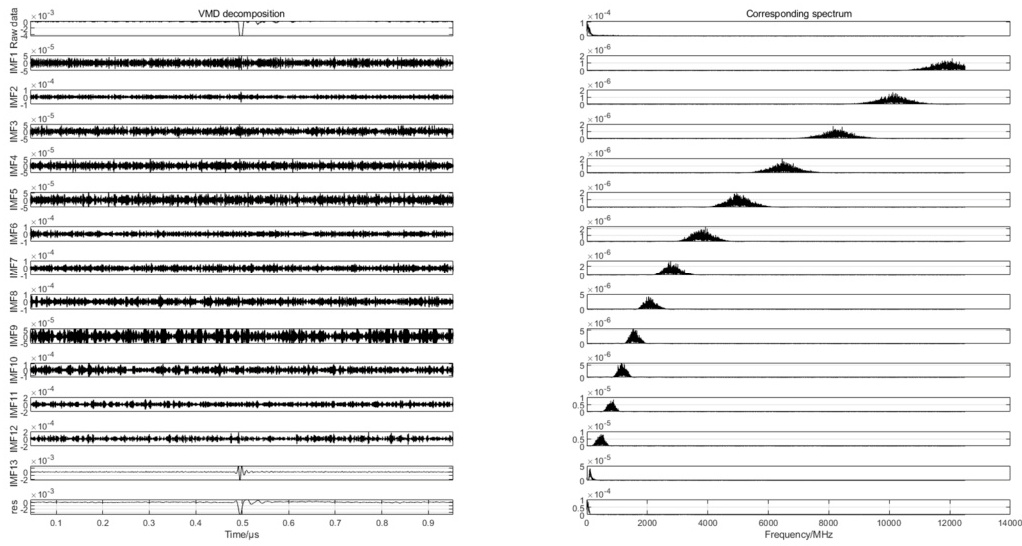
2. 分析要点
- 频率聚集性:正常分解下各IMF频谱应无重叠,否则需调整KK或αα。
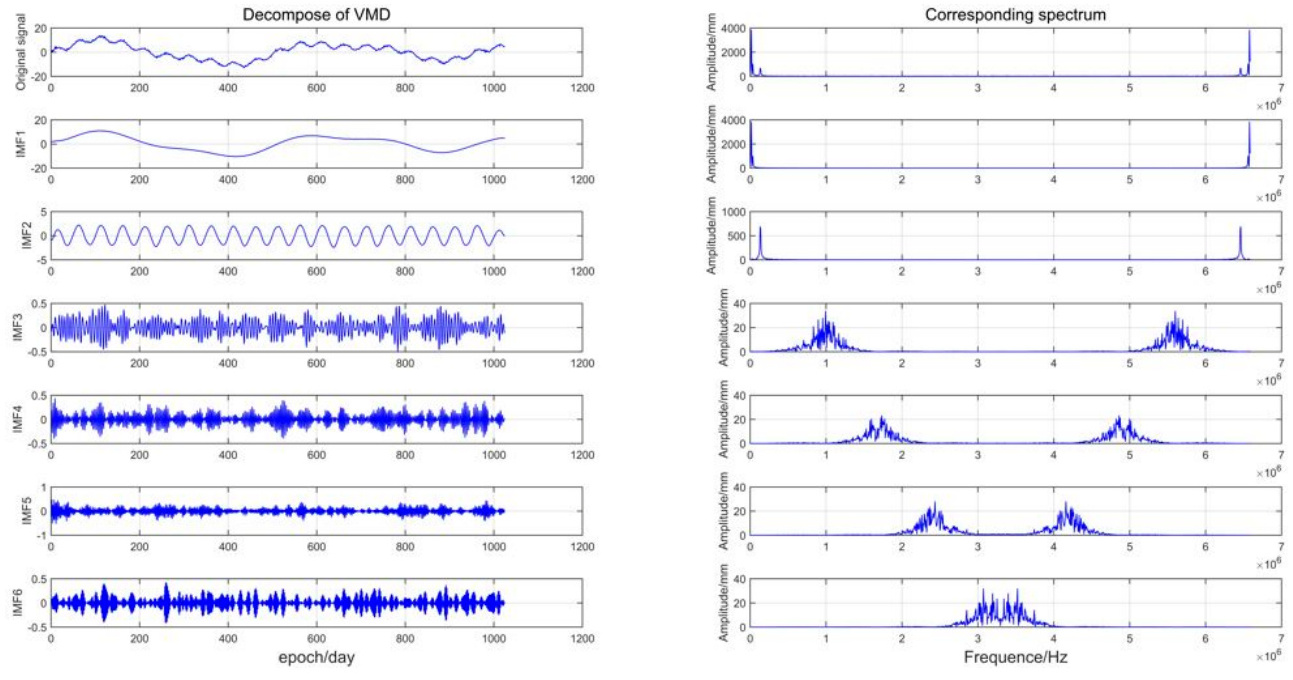
- 噪声识别:高频IMF频谱呈现宽带特性,可结合能量熵判断噪声分量。
七、综合应用案例
1. 轴承故障诊断流程
- 信号采集:获取振动加速度信号;
- VMD分解:设置K=5 α=2000,分解得到IMF1\simIMF5;
- 特征提取:
- 计算各IMF的包络熵,选择IMF3(熵值最小);
- 提取IMF3的包络谱,识别fBPFOfBPFO峰值;
- 状态判定:若峭度值K>5且包络谱存在特征频率,判定为外圈故障。
2. 光伏功率预测
- 分解时序数据:VMD将功率序列分解为趋势项与周期项;
- 熵特征筛选:利用样本熵选择高复杂度分量输入LSTM模型。
八、局限性与改进方向
- 参数敏感性问题:KK和αα依赖经验选择,可结合优化算法(如粒子群)自适应确定。
- 噪声干扰:VMD无法直接去噪,需结合小波阈值或RDT(随机递减技术)。
- 模态混叠:惩罚因子设置不当导致分量重叠,需联合1.5维谱分析抑制干扰。
通过上述分析,VMD结合多维度特征提取方法,在机械故障诊断、能源预测等领域展现了强大的适用性,未来可进一步与深度学习融合提升自动化分析能力。
📚2 运行结果

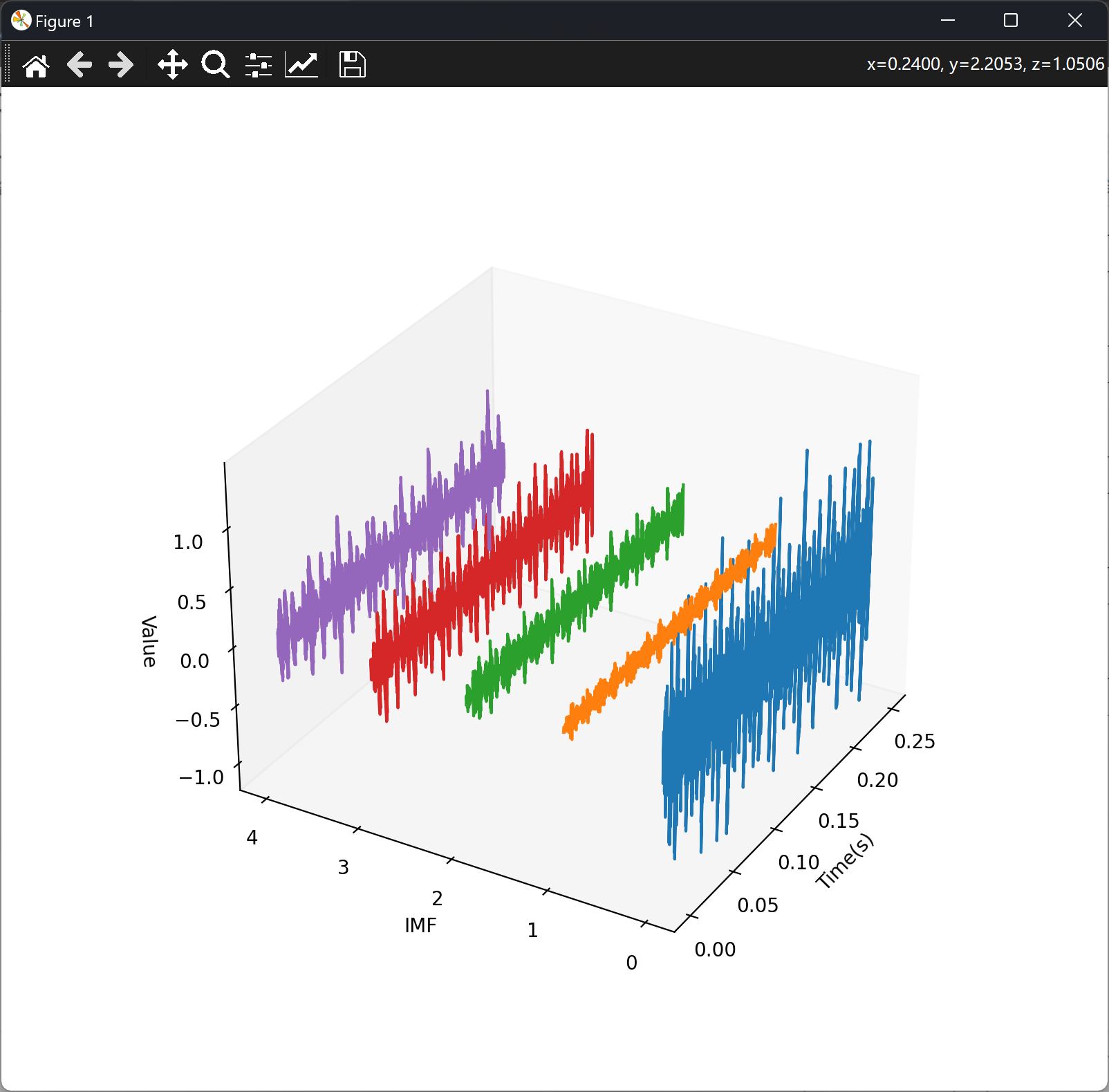





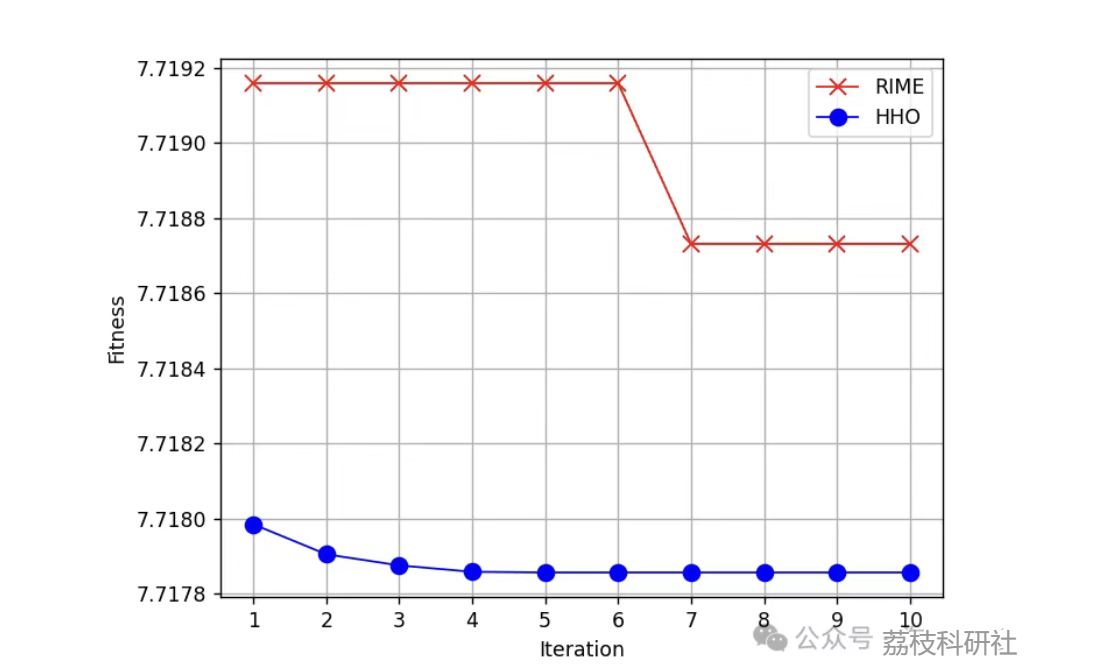
这是哈里斯鹰算法(HHO)和霜冰算法(RIME),适应度函数为最小包络熵的结果:
运行完后在命令行窗口会显示如下结果:

第一个参数为最佳的惩罚因子alpha,第二个为模态分量K。
不得不说,修改起来算法是真的很方便!
再来一个多元宇宙算法(MVO)和斑马算法(ZOA),适应度函数为最小排列熵的结果:


部分代码:
# 调整子图之间的垂直间距和图形标题的位置
plt.subplots_adjust(hspace=3, top=0.95)
plt.show()
# 计算峭度值
kurtosis_values = []
for i in range(K):
kurtosis_value = kurtosis(u[i, :], fisher=False)
kurtosis_values.append(kurtosis_value)
print(f'IMF{i + 1}的峭度值为:{kurtosis_value:.4f}')
# 绘制条形图
plt.figure()
bar_plot = plt.bar(range(1, K+1), kurtosis_values, width=0.3)
plt.xlabel('模态函数', fontproperties=font_prop)
plt.ylabel('峭度值', fontproperties=font_prop)
# 在每个条形的顶部显示峭度值
for i, rect in enumerate(bar_plot):
plt.text(rect.get_x() + rect.get_width() / 2, rect.get_height(), f'{kurtosis_values[i]:.4f}',
ha='center', va='bottom')
# 设置x轴刻度标签
plt.xticks(range(1, K+1), [f'IMF{i}' for i in range(1, K+1)], fontsize=12)
plt.show()
# 计算每个IMF的能量和能量熵🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(文章内容仅供参考,具体效果以运行结果为准)
[1]张彬桥,舒勇,江雨.基于改进变分模态分解和优化堆叠降噪自编码器的轴承故障诊断[J].计算机集成制造系统, 2024, 30(4):1408-1421.
[2]李亚超.基于VMD的滚动轴承故障诊断方法研究[D].石家庄铁道大学[2025-04-06].
[3]王涛,胡定玉,丁亚琦,等.基于经验模式分解和排列熵的轴承故障特征提取[J].噪声与振动控制, 2021, 41(1):77-null.
🌈4 Python代码实现
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取
























 327
327

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








