基于合作型Stackerlberg博弈的考虑差别定价和风险管理的微网运行策略研究（Matlab代码实现）-CSDN博客

本文链接：https://blog.csdn.net/qq_46009436/article/details/148379484

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于合作型Stackelberg博弈的微网运行策略研究框架

一、合作型Stackelberg博弈的核心原理

二、差别定价与风险管理的协同作用机制

三、研究现状与应用案例分析

四、提升微网经济性与稳定性的关键路径

五、未来研究方向

总结

📚2 运行结果

2.1 算例1

2.2 算例2

🎉3 文献来源

🌈4 Matlab代码、数据、文章下载

💥1 概述

文献来源（SCI电气文章）：

本文提出了一种双层能源管理框架，可以帮助零售市场协调多个生产商之间的对等（P2P）能源交易。为此，互动过程被制定为一个合作的Stackelberg博弈模型，其中零售商作为领导者，决定不同消费者的价格歧视，目标是最大化社会福利。另一方面，生产者充当追随者，以合作的方式对领导者的决定做出反应。基于一般纳什讨价还价方案，生产者参与P2P能源交易，与邻居共享其闲置能源，同时根据贡献分配合作收入。考虑到可再生能源的不确定性，采用具有条件风险值（CVaR）的随机规划方法来描述零售商的预期损失。将分层能量相互作用公式化为一个非线性双层规划模型，提出了一种两阶段方法来解决在较低层具有幂函数的公式。在第一阶段，利用Karush-Kuhn-Tucker条件，将一个双层模型转化为一个等价的单层混合整数线性规划问题。此外，第二阶段完成市场清算，并根据调度结果确定生产商的付款。通过数值算例验证了该模型的有效性。

分布式能源（DER）和储能系统的部署允许传统消费者成为生产商拥有这些基础设施的消费者有能力管理他们的发电和消费。考虑到上网电价，生产者可以与配电网（DN）进行能源交易，以保持供需的动态平衡[1]。它还为能源市场和消费者提供了灵活性和可靠性，并提高了整个系统的社会效益[2]。然而，间歇性DER的存在给电力系统实现平衡带来了挑战[3]。为了减少对电网的干扰，需要一种适当的能源管理技术，以使生产者能够在当地共享能源资源。

文献中有几项努力来解决与零售价格相关的第一个挑战。在领导者-追随者结构中，电价和电量始终被设置为交互变量。两种有效的测量方法，包括市场竞价和动态定价，用于确定价格和协调ET。对于前一组，生产商被分为卖方或买方，在固定角色下，在他们之间进行招标[8-10]具体而言，卖家作为领导者，决定价格，而买家做出反应并改变其运营策略[8,11]。相反，卖家向买家公布他们的可用能量，买家给出他们想要支付的最佳价格[9,10]。由于生产商是一个在内部安装可再生能源和负载的实体，因此在生产过程中消耗电力。根据净电力情况，生产商可以在日常时间内充当卖方或买方。因此，由于参与者的角色是预先确定的，市场竞价不能充分捕捉生产商的灵活性，这可能会浪费闲置资源并增加不必要的成本。为了使生产者拥有参与P2P ET的同等特权，交易平台被用作拍卖人，以确定买家和卖家的拍卖价格和能量量[12]。

如图1所示，我们考虑一个零售商和一组生产商的能源管理问题。通常，问题被表述为Stackelberg博弈模型，其中确定了两种类型的参与者，即领导者（零售商）和追随者（生产商）。作为中间人，零售商有权确定价格，以促进主电网和生产商之间的能源交易

在主电网的支持下，由风力发电、电池和负载组成的每个生产商相互作用，以保持供需平衡。在所提出的模型中，采用随机规划方法来解决不确定性，其中发电输出的不确定性由离散场景捕获

零售商做出决策以帮助DN实现可靠的运营并减少干扰，例如与价格设置相关的干扰。由于生产者也是理性和自私的，因此参与能源管理在很大程度上取决于他们的意愿。与统一价格不同，零售商提供价格歧视技术，使消费者成为能源管理的一个组成部分。为了解决不确定性，提出了一种决策模型，供零售商利用CVaR从全球角度控制总体风险水平[33]

在观察零售商的决定后，生产商相互协商，以对零售价格做出综合反应。

基于合作型Stackelberg博弈的微网运行策略研究框架

一、合作型Stackelberg博弈的核心原理

合作型Stackelberg博弈是一种分层决策模型，由领导者（Leader）和合作型跟随者（Followers）构成。领导者率先制定策略，跟随者通过协同决策响应领导者，形成均衡解。其存在性和唯一性需满足以下条件：

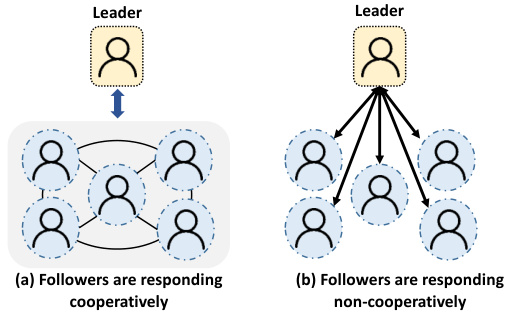
策略集性质：所有参与者的策略空间需为非空、封闭、有界的凸集。
最优响应唯一性：领导者与跟随者的最佳策略需互为唯一解。
目标函数凸性：各方的收益函数需满足凸性条件以保证均衡稳定性。

在微网场景中，微网运营商（MGO）作为领导者，制定电价策略与能源调度计划；用户或分布式能源供应商作为跟随者，根据电价调整用电行为或能源交易策略，双方通过动态博弈实现整体利益最大化。

二、差别定价与风险管理的协同作用机制

差别定价策略
- 动态分时电价：根据负荷需求时段（峰、平、谷）制定阶梯电价，引导用户转移用电高峰。例如，工业用户在高峰时段电价上调20%，居民用户在低谷时段电价下调15%。
- 用户类别差异化：针对工业、商业、居民用户设计不同电价结构，反映其需求弹性和用电特性。例如，高耗能企业执行惩罚性电价以促进能效提升。
- 可再生能源溢价：对光伏、风电等绿色能源给予补贴电价，激励清洁能源消纳。
风险管理方法
- 条件风险价值（CVaR） ：量化极端场景下的预期损失，优化储能充放电策略以平滑可再生能源波动。例如，通过CVaR约束将风光出力不确定性导致的预期损失控制在5%以内。
- 鲁棒优化：考虑最坏情况下的供需平衡，设计保守但鲁棒的调度方案。例如，在风光出力预测误差±20%时，仍能保证微网稳定运行。
- 场景分析法：生成多场景（如极端天气、市场电价波动）模拟风险，并通过概率权重优化决策。
协同优化框架
- 双层模型结构：

上层（MGO） ：以总收益最大化为目标，结合CVaR风险指标优化电价与能源调度计划。
下层（用户） ：根据电价信号调整用电行为，形成负荷需求反馈。
- 博弈均衡求解：通过KKT条件将双层模型转换为单层数学规划问题，利用遗传算法或CPLEX求解。

三、研究现状与应用案例分析

典型研究模型
- 源-网-荷博弈：微网内部能源管理中心（MEMC）作为领导者，协调分布式电源（DG）与用户间的交易，通过Stackelberg博弈实现供需动态平衡。
- 多微网联盟：多个微网形成联盟，通过主从博弈优化跨微网的能量互济，降低整体运行成本。
- 虚拟电厂（VPP） ：结合Stackelberg博弈与合作博弈，协调VPP与外部电网的交易策略，提升低碳经济性。
实际应用案例
- 印度泵式蓄能储能（PHES） ：通过差别定价机制实现能源套利，高峰时段电价溢价30%，低谷时段消纳过剩风电。
- 中国多站融合微电网：采用Stackelberg博弈优化储能与分布式电源的协同调度，风光消纳率提升12%，运行成本降低8%。
- 欧洲合同差异定价（CfD） ：基于历史电价制定可再生能源溢价，平衡市场波动风险与投资回报。

四、提升微网经济性与稳定性的关键路径

差别定价与风险管理的协同效应
- 经济性提升：通过分时电价引导负荷削峰填谷，减少高价时段外购电成本，同时通过CVaR约束降低极端风险损失。
- 稳定性增强：鲁棒优化结合储能调度，平抑风光出力波动，保障孤岛模式下的频率与电压稳定。
算法与模型创新
- 混合整数二次规划（MIQP） ：将风光不确定性建模为机会约束，提升求解效率。
- 多智能体深度强化学习：结合Stackelberg博弈与Q-learning，实现动态策略自适应优化。
政策与技术融合
- 碳交易机制：引入阶梯碳价激励微网低碳化，每吨CO₂排放成本增加50元可推动储能利用率提升10%。
- 动态补贴机制：根据用户响应度调整补贴，例如需求响应参与度每提高1%，电价折扣增加0.5%。