机器学习实验之糖尿病预测

已于 2023-02-01 12:54:54 修改
阅读量2.2w 收藏
点赞数 20
分类专栏： 机器学习 文章标签： 人工智能 python
于 2022-05-27 17:55:44 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_46039856/article/details/125008619
版权

文章目录

机器学习实验之糖尿病预测

实验内容：

diabetes 是一个关于糖尿病的数据集， 该数据集包括442个病人的生理数据及一年以后的病情发展情况。

该数据集共442条信息，特征值总共10项, 如下:

age:年龄

sex:性别

bmi(body mass index):身体质量指数，是衡量是否肥胖和标准体重的重要指标，理想BMI(18.5~23.9) = 体重(单位Kg) ÷ 身高的平方 (单位m)

bp(blood pressure):血压（平均血压）

s1,s2,s3,s4,s4,s6:六种血清的化验数据，是血液中各种疾病级数指针的6的属性值。

s1——tc，T细胞（一种白细胞）
s2——ldl，低密度脂蛋白
s3——hdl，高密度脂蛋白
s4——tch，促甲状腺激素
s5——ltg，拉莫三嗪
s6——glu，血糖水平

【注意】：以上的数据是经过特殊处理， 10个数据中的每个都做了均值中心化处理，然后又用标准差乘以个体数量调整了数值范围。验证就会发现任何一列的所有数值平方和为1。

   这10个特征变量中的每一个都以平均值为中心，并按标准差乘以“n_samples”（即每列的平方和总计为1）进行缩放。

实验要求：

一、加载糖尿病数据集diabetes，观察数据

1.载入糖尿病情数据库diabetes，查看数据。

2.切分数据，组合成DateFrame数据，并输出数据集前几行，观察数据。

二、基于线性回归对数据集进行分析

3.查看数据集信息，从数据集中抽取训练集和测试集。

4.建立线性回归模型，训练数据，评估模型。

三、考察每个特征值与结果之间的关联性，观察得出最相关的特征

5.考察每个特征值与结果之间的关系，分别以散点图展示。

思考：根据散点图结果对比，哪个特征值与结果之间的相关性最高？

四、使用回归分析找出XX特征值与糖尿病的关联性，并预测出相关结果

6.把5中相关性最高的特征值提取，然后进行数据切分。

8.创建线性回归模型，进行线性回归模型训练。

9.对测试集进行预测，求出权重系数。

10.对预测结果进行评价，结果可视化。

from jupyterthemes import jtplot
jtplot.style(theme='monokai') #选择一个绘图主题
from sklearn.datasets import load_diabetes
import matplotlib.pyplot as plt  #导入matplotlib库
import numpy as np      #导入numpy库
import pandas as pd     #导入pandas库

加载糖尿病数据集diabetes，观察数据

载入糖尿病情数据库diabetes，查看数据

diabetes = load_diabetes()
keys = diabetes.keys()
print(keys)
data = diabetes.data
print(data)
target = diabetes.target
print(target)
feature_names = diabetes.feature_names
print(feature_names)

dict_keys(['data', 'target', 'frame', 'DESCR', 'feature_names', 'data_filename', 'target_filename', 'data_module'])
[[ 0.03807591  0.05068012  0.06169621 ... -0.00259226  0.01990842
  -0.01764613]
 [-0.00188202 -0.04464164 -0.05147406 ... -0.03949338 -0.06832974
  -0.09220405]
 [ 0.08529891  0.05068012  0.04445121 ... -0.00259226  0.00286377
  -0.02593034]
 ...
 [ 0.04170844  0.05068012 -0.01590626 ... -0.01107952 -0.04687948
   0.01549073]
 [-0.04547248 -0.04464164  0.03906215 ...  0.02655962  0.04452837
  -0.02593034]
 [-0.04547248 -0.04464164 -0.0730303  ... -0.03949338 -0.00421986
   0.00306441]]
[151.  75. 141. 206. 135.  97. 138.  63. 110. 310. 101.  69. 179. 185.
 118. 171. 166. 144.  97. 168.  68.  49.  68. 245. 184. 202. 137.  85.
 131. 283. 129.  59. 341.  87.  65. 102. 265. 276. 252.  90. 100.  55.
  61.  92. 259.  53. 190. 142.  75. 142. 155. 225.  59. 104. 182. 128.
  52.  37. 170. 170.  61. 144.  52. 128.  71. 163. 150.  97. 160. 178.
  48. 270. 202. 111.  85.  42. 170. 200. 252. 113. 143.  51.  52. 210.
  65. 141.  55. 134.  42. 111.  98. 164.  48.  96.  90. 162. 150. 279.
  92.  83. 128. 102. 302. 198.  95.  53. 134. 144. 232.  81. 104.  59.
 246. 297. 258. 229. 275. 281. 179. 200. 200. 173. 180.  84. 121. 161.
  99. 109. 115. 268. 274. 158. 107.  83. 103. 272.  85. 280. 336. 281.
 118. 317. 235.  60. 174. 259. 178. 128.  96. 126. 288.  88. 292.  71.
 197. 186.  25.  84.  96. 195.  53. 217. 172. 131. 214.  59.  70. 220.
 268. 152.  47.  74. 295. 101. 151. 127. 237. 225.  81. 151. 107.  64.
 138. 185. 265. 101. 137. 143. 141.  79. 292. 178.  91. 116.  86. 122.
  72. 129. 142.  90. 158.  39. 196. 222. 277.  99. 196. 202. 155.  77.
 191.  70.  73.  49.  65. 263. 248. 296. 214. 185.  78.  93. 252. 150.
  77. 208.  77. 108. 160.  53. 220. 154. 259.  90. 246. 124.  67.  72.
 257. 262. 275. 177.  71.  47. 187. 125.  78.  51. 258. 215. 303. 243.
  91. 150. 310. 153. 346.  63.  89.  50.  39. 103. 308. 116. 145.  74.
  45. 115. 264.  87. 202. 127. 182. 241.  66.  94. 283.  64. 102. 200.
 265.  94. 230. 181. 156. 233.  60. 219.  80.  68. 332. 248.  84. 200.
  55.  85.  89.  31. 129.  83. 275.  65. 198. 236. 253. 124.  44. 172.
 114. 142. 109. 180. 144. 163. 147.  97. 220. 190. 109. 191. 122. 230.
 242. 248. 249. 192. 131. 237.  78. 135. 244. 199. 270. 164.  72.  96.
 306.  91. 214.  95. 216. 263. 178. 113. 200. 139. 139.  88. 148.  88.
 243.  71.  77. 109. 272.  60.  54. 221.  90. 311. 281. 182. 321.  58.
 262. 206. 233. 242. 123. 167.  63. 197.  71. 168. 140. 217. 121. 235.
 245.  40.  52. 104. 132.  88.  69. 219.  72. 201. 110.  51. 277.  63.
 118.  69. 273. 258.  43. 198. 242. 232. 175.  93. 168. 275. 293. 281.
  72. 140. 189. 181. 209. 136. 261. 113. 131. 174. 257.  55.  84.  42.
 146. 212. 233.  91. 111. 152. 120.  67. 310.  94. 183.  66. 173.  72.
  49.  64.  48. 178. 104. 132. 220.  57.]
['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']

切分数据，组合成DateFrame数据，并输出数据集前几行，观察数据

df = pd.DataFrame(data,columns = feature_names)
df.head()
agesexbmibps1s2s3s4s5s6
00.0380760.0506800.0616960.021872-0.044223-0.034821-0.043401-0.0025920.019908-0.017646
1-0.001882-0.044642-0.051474-0.026328-0.008449-0.0191630.074412-0.039493-0.068330-0.092204
20.0852990.0506800.044451-0.005671-0.045599-0.034194-0.032356-0.0025920.002864-0.025930
3-0.089063-0.044642-0.011595-0.0366560.0121910.024991-0.0360380.0343090.022692-0.009362
40.005383-0.044642-0.0363850.0218720.0039350.0155960.008142-0.002592-0.031991-0.046641

基于线性回归对数据集进行分析

查看数据集信息，从数据集中抽取训练集和测试集

from sklearn.model_selection import train_test_split  #导入数据划分包 
x_train,x_test,y_train,y_test=train_test_split(data,target,train_size=0.25)
x_train.shape,x_test.shape,y_train.shape,y_test.shape

((110, 10), (332, 10), (110,), (332,))

建立线性回归模型，训练数据，评估模型

from sklearn.linear_model import LinearRegression
model = LinearRegression() # 建立模型
model.fit(x_train,y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
model.score(x_train,y_train) # 评估模型


0.42370530869688006

考察每个特征值与结果之间的关联性，观察得出最相关的特征

考察每个特征值与结果之间的关系，分别以散点图展示。

# 作图5行2列的图
plt.figure(figsize=(2*10,5*8))
# enumerate 枚举 相当于 
# for j in df.columns:
#     i+=1
result = {}
for i,j in enumerate(df.columns):  
#     print(i , j) 
    train_y = target
    train_x = df.loc[:,j].values.reshape(-1, 1)
    linear_model = LinearRegression()    # 构建模型
    linear_model.fit(train_x,train_y)    #训练模型
    score = linear_model.score(train_x,train_y)   # 评估模型
    axes = plt.subplot(5,2,i+1)
    plt.scatter(train_x,train_y,color="blue")
    axes.set_title("the result of " + j + " is " + str(score))
    result[j] = score
    plt.scatter(train_x,train_y)
#     # 画拟合直线
#     k =  linear_model.coef_     # 回归系数
#     b =  linear_model.intercept_   # 截距
#     x = np.linspace(train_x.min(),train_x.max(),100)
#     y = x * k + b
#     plt.plot(x,y,c='red')
print(result)

{'age': 0.03530218264671636, 'sex': 0.0018543357106460823, 'bmi': 0.3439237602253803, 'bp': 0.19490798886682947, 's1': 0.04495353245556555, 's2': 0.030294651136685613, 's3': 0.1558585524453051, 's4': 0.18528968598509687, 's5': 0.32022405096453443, 's6': 0.14629361572293453}

46546456

import operator
result = sorted(result.items(),key=operator.itemgetter(1),reverse=True)
resMax = result[0]
print("The greatest impact on diabetes is",resMax[0])
print("corresponding coefficient of determination is",resMax[1])

The greatest impact on diabetes is bmi
corresponding coefficient of determination is 0.3439237602253803

使用回归分析找出bmi特征值与糖尿病的关联性，并预测出相关结果

把相关性最高的特征值提取，然后进行数据切分

diabetes = load_diabetes()
df = pd.DataFrame(diabetes.data,columns = diabetes.feature_names)
y = target
x = df.loc[:,'bmi'].values.reshape(-1, 1)
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.25)

创建线性回归模型，进行线性回归模型训练

linear_model = LinearRegression()    # 构建模型
linear_model.fit(train_x,train_y)    # 训练模型

LinearRegression()

对测试集进行预测，求出权重系数

y_hat = linear_model.predict(x_test) # 对测试集的预测
print("the Weight factor is", linear_model.coef_[0])

the Weight factor is 619.2228206843333

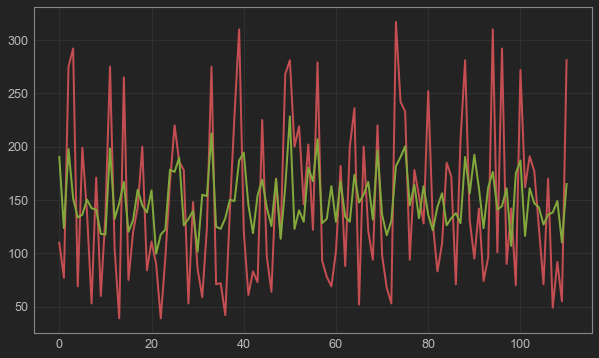
对预测结果进行评价，结果可视化

#y_test与y_hat的可视化
plt.figure(figsize=(10,6))  #设置图片尺寸
t = np.arange(len(x_test))  #创建t变量

plt.plot(t, y_test, 'r', linewidth=2, label='y_test') #绘制y_test曲线
plt.plot(t, y_hat, 'g', linewidth=2, label='y_hat')   #绘制y_hat曲线
plt.show()

8528521

plt.figure(figsize=(10,6))   #绘制图片尺寸
plt.plot(y_test,y_hat,'o',color='blue')   #绘制散点
plt.plot([30,320],[30,320], color="red", linestyle="--", linewidth=1.5) 
plt.axis([30,320,30,320])
plt.xlabel('ground truth')   #设置X轴坐标轴标签
plt.ylabel('predicted')      #设置y轴坐标轴标签
plt.grid()  #绘制网格线

485464545

from sklearn import metrics
from sklearn.metrics import r2_score
# 拟合优度R2的输出方法一
print ("r2:",linear_model.score(x_test, y_test))  #基于Linear-Regression()的回归算法得分函数，来对预测集的拟合优度进行评价
# 拟合优度R2的输出方法二
print ("r2_score:",r2_score(y_test, y_hat)) #使用metrics的r2_score来对预测集的拟合优度进行评价
# 用scikit-learn计算MAE
print ("MAE:", metrics.mean_absolute_error(y_test, y_hat)) #计算平均绝对误差
# 用scikit-learn计算MSE
print ("MSE:", metrics.mean_squared_error(y_test, y_hat))  #计算均方误差
# # 用scikit-learn计算RMSE
print ("RMSE:", np.sqrt(metrics.mean_squared_error(y_test, y_hat))) #计算均方根误差

r2: 0.27725246428335715
r2_score: 0.27725246428335715
MAE: 55.71388594300793
MSE: 4181.8215824825365
RMSE: 64.66700536195052
【Python数据挖掘课程】五.线性回归知识及预测糖尿病实例
杨秀璋的专栏
10-28 3万+
今天主要讲述的内容是关于一元线性回归的知识，Python实现，包括以下内容： 1.机器学习常用数据集介绍 2.什么是线性回顾 3.LinearRegression使用方法 4.线性回归判断糖尿病 同时这篇文章是我上课的内容，所以参考了一些知识，强烈推荐大家学习斯坦福的机器学习Ng教授课程和Scikit-Learn中的内容。由于自己数学不是很好，自己也还在学习中，所以文章以代码和一元线性回归为主，数学方面的当自己学到一定的程度，才能进行深入的分享
02_基于线性回归预测糖尿病
奔腾游子
04-07 3923
基于线性回归预测糖尿病 1、实验描述 使用Python编程，利用diabetes dataset，一个糖尿病数据集，主要包括442行数据，10个属性值，分别是：Age(年龄)、性别(Sex)、Body mass index(体质指数)、Average Blood Pressure(平均血压)、S1~S6一年后疾病级数指标。Target为一年后患疾病的定量指标。首先将数据集划分为训练集和测试集，创建线性回归模型，然后训练数据集，得到每个特征下的参数。绘图表示出真实值和预测值之间的对比。 实验时长：35
基于机器学习的糖尿病分析与预测
最新发布
weixin_67879842的博客
03-16 1433
通过合理数据分析、特征工程以及模型构建工作，构建多种模型合理预测糖尿病。
线性回归-糖尿病预测
weixin_48434899的博客
03-29 1万+
实验内容:糖尿病预测 diabetes 是一个关于糖尿病的数据集， 该数据集包括442个病人的生理数据及一年以后的病情发展情况。 该数据集共442条信息，特征值总共10项, 如下: age:年龄 sex:性别 bmi(body mass index):身体质量指数，是衡量是否肥胖和标准体重的重要指标，理想BMI(18.5~23.9) = 体重(单位Kg) ÷ 身高的平方 (单位m) bp(blood pressure):血压（平均血压） s1,s2,s3,s4,s4,s6:六种血清的化验数据，是血液
燕山大学机器学习实验一：线性回归1——糖尿病情预测
weixin_51556077的博客
01-01 4866
实操项目 1——糖尿病情预测 实验要求 一、加载糖尿病数据集 diabetes，观察数据 1.载入糖尿病情数据库 diabetes，查看数据。 2.切分数据，组合成 DateFrame 数据，并输出数据集前几行，观察数据。 二、基于线性回归对数据集进行分析 3.查看数据集信息，从数据集中抽取训练集和测试集。 4.建立线性回归模型，训练数据，评估模型。 三、考察每个特征值与结果之间的关联性，观察得出最相关的特征 5.考察每个特征值与结果之间的关系，分别以散点图展示。 思考：根据散点图结果对比，哪个特征值与结果
Python机器学习预测糖尿病
2301_78297473的博客
05-11 4961
因此，提取做好糖尿病的筛查与预警尤为重要，本系统基于机器学习算法，为用户提供了一个可以自行筛查糖尿病的预警系统，可以让用户早发现，早治疗，避免诸多糖尿病以及并发症的困扰，提高每一位患者的生活质量。如果控制不好的话，患者从头到脚、由内到外、从肉体到精神几乎无一幸免，其对患者的影响是多方面的、严重的和终身性的，与之相伴的还有长期高额的医疗支出，但最终患者还是难逃致残和早亡的结局，说糖尿病是“百病之源”可谓实至名归。样本集合中，如果所有类别的样本概率相同，那么此时“混乱程度”最高，信息熵为logk，取到最大值。
用线性回归进行糖尿病预测
不凡De老五
12-12 5991
1.导入模块 2.获取训练数据 3.创建学习模型 4.训练数据 5.预测结果 6.效果评估 7.绘图
基于机器学习算法的糖尿病预测模型研究
04-27
本文在总结前人研究的基础上，对导致糖尿病的危险因素...所以，最终选择以网络结构为 7-1-1 的人工神经网络模型为本研究中糖尿病预测的最适模型。 关键词：糖尿病；危险因素；BP 人工神经网络；支持向量机；集成学习
机器学习算法在糖尿病预测中的应用 (1).pdf
09-24
机器学习算法在糖尿病预测中的应用是机器学习技术在医学领域的重要应用之一。糖尿病是多发病和严重的慢性病，患病率呈现逐步上升的趋势。机器学习算法可以对糖尿病进行预测，从而帮助医生更好地诊断和治疗糖尿病。 ...
燕山大学机器学习实验代码
05-30
机器学习实验之不同含量果汁饮料的聚类（K-Means） 机器学习实验之肿瘤预测与分析（神经网络） 机器学习实验之肿瘤预测（决策树） 机器学习实验之顾客购买服装的分析与预测 ...机器学习实验之糖尿病预测
使用机器学习技术预测糖尿病-研究论文
06-10
在本研究中，使用了六种流行的机器学习技术，即随机森林 (RF)、逻辑回归 (LR)、朴素贝叶斯 (NB)、C4.5 决策树 (DT)、K-最近邻 (KNN) 和支持向量比较机器 (SVM) 以获得出色的机器学习技术来预测糖尿病。 我们的新...
【线性回归、岭回归、Lasso回归分别预测患者糖尿病病情】数据挖掘实验一
Lenhart001的博客
09-18 2853
（详细描述数据集：如特征属性名称及意义、记录数等）（写出项目中涉及的主要算法原理及模型评价方法）
糖尿病预测机器学习项目指南
weixin_34618526的博客
10-06 2012
本文还有配套的精品资源，点击获取 简介："Diabetes-Predictor" 是一个结合数据分析与机器学习技术的项目，致力于通过生理指标预测糖尿病风险。该项目采用Jupyter Notebook进行数据处理、模型构建与验证，并包含特征工程、模型选择、性能评估和模型部署等环节。开发者将利用公开数据集（如Pima Indians Diabetes Dataset）进行探索性...
机器学习算法构建预测糖尿病模型
2301_77801940的博客
06-25 3913
世界卫生组织近日发布报告称，糖尿病患者的数量正以惊人的速度增长，目前全球每年约有320万人死于糖尿病导致的并发症。本项目旨在通过机器学习算法构建预测糖尿病模型。这段代码展示了一个完整的机器学习项目流程，从数据加载和探索性分析开始，到数据预处理、特征工程、模型选择和评估，最后使用主成分分析和支持向量机进行建模和优化。
【毕业设计】基于机器学习与大数据的糖尿病预测
热门推荐
HUXINY的博客
09-03 2万+
本项目以体检数据集为样本进行了机器学习的预测，但是需要注意几个问题：体检数据量太少，仅有1006条可分析数据，这对于糖尿病预测来说是远远不足的，所分析的结果代表性不强。这里的数据糖尿病和正常人基本相当，而真实的数据具有很强的不平衡性。也就是说，糖尿病患者要远少于正常人，这种不平衡的数据集给真实情况下糖尿病的预测带来了很大困难，当然可以通过上采样、下采样或者其他方法进行不平衡数据集的预测。缺少时序数据使得预测变得不准确，时序数据更能够体现一个人的身体状态。
机器学习实战6-糖尿病疾病的预测与分析(随机森林算法）
微学AI的博客
05-12 3895
大家好，我是微学AI，今天给大家介绍一下机器学习实战6-糖尿病疾病的预测与分析(随机森林算法），糖尿病是一种常见的慢性代谢性疾病，由于生活方式及基因等因素的影响，全球范围内糖尿病患者人数不断增加。预测糖尿病的发生有助于早期筛查和干预治疗，以降低糖尿病带来的危害。糖尿病的预测问题可以看作是一个二分类问题：对于某个人的特征数据，根据其是否患有糖尿病进行分类预测。常用的算法包括逻辑回归、支持向量机、决策树等。
《scikit-learn机器学习》糖尿病预测（KNN）
Bessie_Lee
11-07 7606
本章看完以后的感受： 1、我们先对数据进行加载，由于确定了数据是没有问题的，所以不用对数据进行清洗 2、然后确定每行每列，找到我们需要的目标值，也就是target，在本书中的target为0或者1 3、找到目标值以后，将目标值与非目标值分离，再将数据按照比例分为测试集和训练集。 4、选择的是knn的三种模型，一种是原基础的knn，一种是带有权重的knn，还有一种是确定了半径的knn（上一篇中的knn的俩个变异就是后面的这俩种） 5、然后对他们三个进行训练集训练，选取最佳的一个模型，在对模型进行训练，通过学
线性回归糖尿病预测
m0_74261473的博客
10-30 920
平均绝对误差： 38.258451263442346。中值绝对误差: 32.600475193580735。可解释方差值： 0.5891056346459892。均方误差： 2257.798900123449。R方值： 0.585114043418069。
spark糖尿病预测
02-19
### 如何使用 Apache Spark 实现糖尿病预测模型 #### 数据预处理阶段 为了构建有效的糖尿病预测模型，数据预处理是一个至关重要的环节。这涉及到加载和清理数据集，去除缺失值或异常值，并转换数据格式以便于后续分析。具体来说，在探索糖尿病数据集中，会先对数据进行初步观察，识别可能影响健康状况的因素，如年龄、体重指数(BMI)等指标[^2]。 ```python from pyspark.sql import SparkSession spark = SparkSession.builder.appName('diabetes_prediction').getOrCreate() # 加载CSV文件作为DataFrame data_path = 'path_to_diabetes_dataset.csv' df = spark.read.option("header", "true").option("inferSchema", "true").csv(data_path) # 显示前几条记录查看数据结构 df.show(5) ``` #### 特征工程与准备 特征工程对于提高机器学习模型性能至关重要。在这个过程中，将通过`StringIndexer`来索引分类变量；利用`VectorAssembler`把不同列组合成单一特征向量用于训练模型。此外，还会考虑实施降维技术以减少维度灾难带来的负面影响，从而提升效率并改善泛化能力。 ```python from pyspark.ml.feature import StringIndexer, VectorAssembler # 对类别型字段做索引操作 indexers = [StringIndexer(inputCol=column, outputCol=column+"_indexed") \ .fit(df) for column in list(set(['Outcome']))] pipeline = Pipeline(stages=indexers) indexed_df = pipeline.fit(df).transform(df) # 组合所有数值型特征至单个向量 assembler = VectorAssembler( inputCols=['Pregnancies', 'Glucose', 'BloodPressure', 'SkinThickness', 'Insulin', 'BMI', 'DiabetesPedigreeFunction', 'Age'], outputCol="features") final_data = assembler.transform(indexed_df) ``` #### 模型选择与评估 在准备好输入特征之后，可以尝试多种不同的分类算法来进行比较，比如逻辑回归(Logistic Regression)，随机森林(Random Forest Classifier)或是梯度提升树(Gradient Boosting Trees)[^2]。这里展示了一个简单的例子——采用LogisticRegression建立二元分类器： ```python from pyspark.ml.classification import LogisticRegression from pyspark.ml.evaluation import BinaryClassificationEvaluator from pyspark.ml.tuning import ParamGridBuilder, CrossValidator # 定义LR模型 lr = LogisticRegression(labelCol='Outcome_indexed') # 设置交叉验证参数网格 param_grid = (ParamGridBuilder() .addGrid(lr.regParam, [0.1, 0.01]) .build()) cv = CrossValidator(estimator=lr, estimatorParamMaps=param_grid, evaluator=BinaryClassificationEvaluator(), numFolds=3) model = cv.fit(final_data) best_model = model.bestModel # 测试集上的表现评测 predictions = best_model.transform(test_set) evaluator = BinaryClassificationEvaluator(rawPredictionCol="rawPrediction") accuracy = evaluator.evaluate(predictions) print(f'Accuracy on test set: {accuracy}') ```
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

Gettler•Main

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值