电力系统经济运行与控制（下）-ChatGPT4o作答+清华孙宏斌电力系统分析课程

这张图片介绍了发电成本特性的数学模型，主要关注发电成本与输出功率之间的关系。

主要内容：

1. 近似二次曲线：

• 发电成本 (C(P_G)) 与发电机输出功率 (P_G) 之间的关系使用了二次方程：
  [
  C(P_G) = a + b P_G + c P_G^2
  ]
• 其中，a, b, c 是常数，代表不同的参数。
  • (c > 0)：表示该曲线有极小值，并且无极大值。
  • (b > 0)：表示极小值出现在 (P_G > 0) 时。
  • (a > 0)：表示在 (P_G = 0) 时，成本 (C > 0)。

2. 参数的意义：

• c：影响曲线的形状，控制成本的加速增长。
• b：决定最低点的位置，影响成本的上升速率。
• a：表示在最小功率输出 (P_G = 0) 时的成本。

3. 示例：

• 给出了一个300 MW容量的机组的具体成本函数：
  [
  C = 9000 + 450 P_G + 0.1 P_G^2 \ (\text{¥/h})
  ]
  • 这个成本函数表示，发电机组的运行成本由固定成本 (9000) 元、每增加 (P_G) MW 输出增加的 (450 P_G) 元，以及输出功率对成本的二次影响项 (0.1 P_G^2) 元构成。

4. 功率范围：

• 该机组的功率范围在 (150 \leq P_G \leq 300) MW之间。

结论：

这个模型描述了发电成本随功率变化的二次关系，并且可以通过给定的参数对不同发电机组的运营成本进行优化和分析。这种模型对电力系统的调度和经济调度（ED）非常重要，通过计算不同功率输出下的成本，可以帮助系统优化电力生产，减少运营成本。

该张图片介绍了经济调度（Economic Dispatch, ED）的数学模型的一般形式。我们可以从以下几个方面来解析这个模型：

1. 数学问题描述：

• 已知条件： 系统已知各节点的功率需求，并要求求解每台机组的功率输出。
• 目标： 使发电总成本最小。

目标函数表示为：
[
\min_{\mathbf{P_G}} C_T = \sum_{i=1}^m C_i(P_{G_i})
]
其中，(C_T) 为发电总成本，(\mathbf{P_G}) 为各发电机组的功率输出，(C_i(P_{G_i})) 为第 (i) 台机组的发电成本。

2. 约束条件：

• 等式约束： 有功潮流方程，这通常用于描述电力网络中电流流动的约束。
• 不等式约束： 限制发电机组的功率输出范围及线路的功率传输能力。具体包括：
  • 每台机组的功率输出必须在一定的范围内：
    [
    P_{G_i}^{min} \leq P_{G_i} \leq P_{G_i}^{max}, \quad \forall i
    ]
  • 每条支路的传输能力限制：
    [
    |P_{ij}| \leq P_{ij}^{max}, \quad \forall (i, j)
    ]
    其中 (P_{G_i}^{min}) 和 (P_{G_i}^{max}) 分别表示第 (i) 台机组的最小和最大输出功率，(P_{ij}^{max}) 是连接节点 (i) 和节点 (j) 的支路的最大功率传输限制。

3. 模型的高维性：

• 该模型属于大规模非线性规划问题，涉及大量的发电机组和电网约束，因此求解时需要考虑高维度的问题和计算的复杂性。

结论：

这个数学模型的核心目标是通过优化发电机组的功率输出，最小化整个电网的运营成本，同时满足物理约束条件，如发电机的功率输出范围、电力流动的平衡以及输电线路的容量限制。这类优化问题是电力系统调度中的重要课题，涉及到对电力系统运行成本的精细控制。

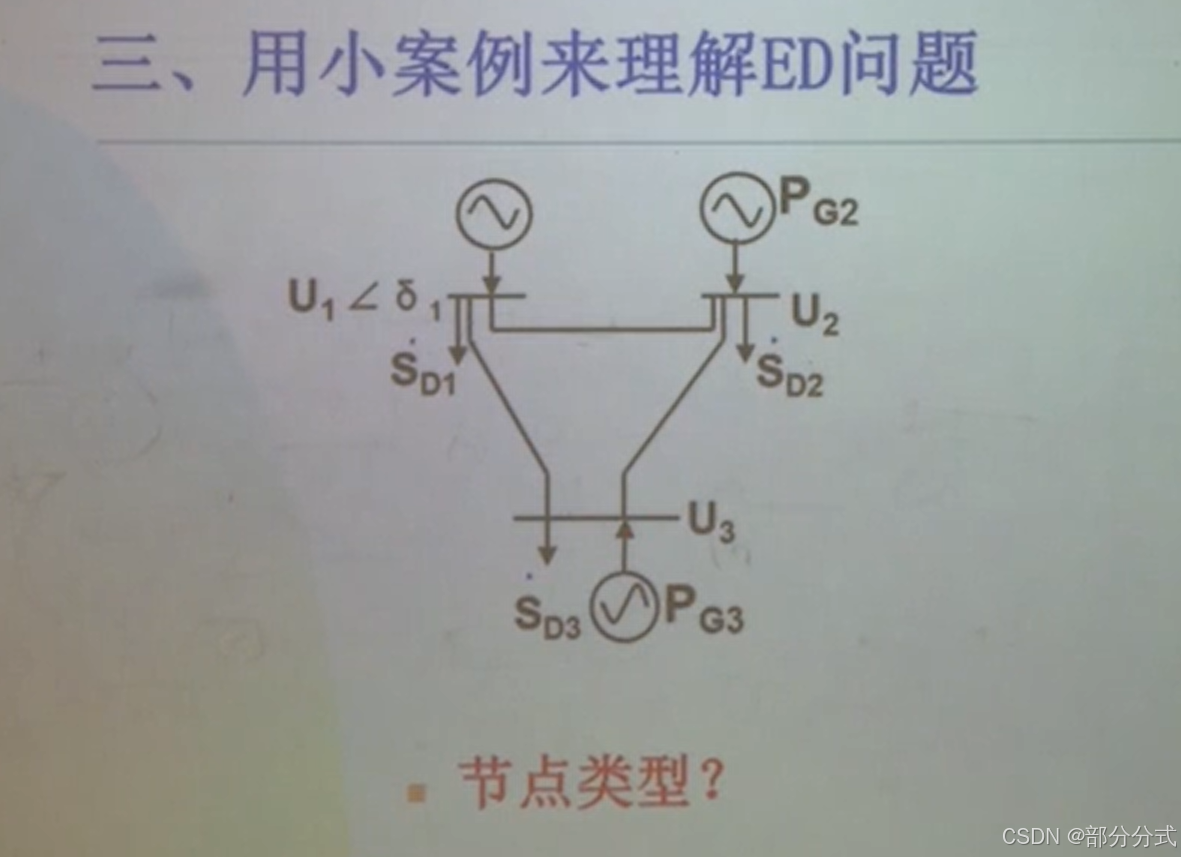
该张图片提供了一个电力系统的示意图，包含三个节点，分别为节点 1、节点 2 和节点 3。每个节点都有电压 (U) 和负载 (S) 以及对应的发电机组 (PG)。图中的问题是根据给出的示意图来理解经济调度 (ED) 的问题。

图示解释：

1. 发电机组：

   • PG2：第二台发电机组，输出功率为 ( P_{G2} )。
   • PG3：第三台发电机组，输出功率为 ( P_{G3} )。

2. 节点：

   • 节点 1 (U1, δ1)：节点 1 的电压为 ( U1 )，并且其相角为 ( \delta1 )。
   • 节点 2 (U2)：节点 2 的电压为 ( U2 )。
   • 节点 3 (U3)：节点 3 的电压为 ( U3 )。

3. 负载：

   • S D1, S D2, S D3：分别是连接节点 1、节点 2 和节点 3 的负载。

节点类型：

从该图可以推测出，节点的类型通常分为三类：

• 发电节点（Generator Node）：具有发电机组输出功率的节点，如节点 1 和节点 2。
• 负载节点（Load Node）：主要消耗电能的节点，在电力系统调度中承担重要的角色。
• 汇流节点（Slack Node）：通常用来平衡功率的流动，确保电力网络的平衡。

关键问题：

• 该系统模型帮助我们理解经济调度问题 (ED)，即在给定负荷需求的情况下，如何最优化各发电机组的功率输出，以最小化总发电成本，同时满足电压和功率平衡等约束条件。

此示意图为电力系统经济调度中的一种基本模型，展示了如何通过不同节点和发电机的功率调度来满足系统需求，并分析各节点在电力调度中的作用。

这张图片展示了一个电力系统中如何进行经济调度（ED）的问题和方法。以下是这张图的内容和分析：

1. 通过潮流计算确定发电机组功率 (P_{G1}) 和支路的功率潮流

• 潮流计算是电力系统分析的核心，用于计算每个节点的电压、支路的功率流向和发电机的输出功率。通过计算得到的发电机组输出功率 (P_{G1})，以及支路的功率流量，用来确认系统是否满足约束条件。

2. 若 (P_{G1}) 和所有支路的功率潮流不满足约束条件

• 如果给定的功率 (P_{G1}) 和系统中的功率潮流不符合电力网络的约束条件，那么需要进行调整。这个过程通常需要根据各个发电机的成本特性，来优化调度，减少总成本。

3. 解优化问题

• 通过求解优化问题，基于各个发电机的成本特性来计算该系统的总成本 (C_T)。
• 这就是所谓的经济调度 (ED)，其目标是最小化整个系统的发电成本，并确保满足负荷需求和系统稳定性。

4. 改变 (P_{G2}) 和 (P_{G3})，得到不同的可行发电组合 (C_T)

• 在系统调度过程中，可以改变其他发电机组 (P_{G2}) 和 (P_{G3}) 的输出，进而得到不同的发电组合，这些组合对应的总成本 (C_T) 会不同。

5. 寻找最小总成本的发电组合

• 通过对所有可能的发电组合进行计算，找到最小总成本的发电方案，这个方案即为经济调度的最优解。

6. 计算方法的物理意义不明确

• 该方法通过计算机模拟与优化求解，但它的物理意义在某些情形下可能并不明确，尤其是在需要进行多变量约束优化时，可能存在计算复杂性问题。

总结来说，这张图片的核心目的是说明如何通过潮流计算和经济调度的优化方法，找到满足电力需求且成本最小的发电机组组合。

这张图片展示了电力系统中经济调度问题（ED）的应用解法，主要是通过最简单的情形来简化分析。

主要内容如下：

1. 问题简化：

• 忽略线路潮流不等式约束：不考虑线路之间的功率流动约束。实际上，线路的容量和流动限制是电力系统中的重要约束条件，在复杂的经济调度模型中需要考虑，但在这个简化的模型中被忽略。
• 忽略网络损耗：在很多情况下，电力系统中存在功率损耗，这通常与电压损失、传输电流等相关。然而，在这个简化的模型中，忽略了这些损耗因素。
• 忽略发电机出力不等式约束：发电机有最大和最小功率输出的限制条件，实际调度中需要确保每个发电机的输出在规定范围内。但在简化的模型中，假设发电机的输出可以在任意范围内。

2. 数学模型简化：

• 目标函数：通过最小化总成本来进行优化，目标函数为：
  [
  min C_T = \sum_{i=1}^m C_i(P_{G_i})
  ]
  其中，( C_i(P_{G_i}) ) 是第i台发电机的成本函数，( P_{G_i} ) 是其发电功率输出。

• 等式约束：总功率输出应该等于负荷需求，即：
  [
  \sum_{i=1}^m P_{G_i} = P_D
  ]
  这是一个功率平衡的约束条件，要求发电机的总功率等于负荷需求。

3. 潮流方程是否需要约束：

• 考虑潮流方程约束：这个问题提出是否需要在经济调度中考虑潮流方程约束，即网络中各个节点的功率流向是否符合电力传输的实际条件。这个问题是值得深思的，因为尽管在简化模型中不考虑潮流约束，但在实际操作中，潮流约束至关重要，影响系统的稳定性与安全性。

总结：

这张图主要展示了一个简化的经济调度问题模型，忽略了一些实际操作中非常重要的约束条件（如潮流约束和损耗），其目标是通过优化发电机的输出功率，最小化总成本。这种简化模型对于理解经济调度的基本概念很有帮助，但在实际应用中，需要更复杂的模型来考虑所有约束条件。

这张图片进一步解释了**经济调度问题（ED）**的解决方法，特别是它的简化版本，主要侧重于最简单的情形。

主要内容：

1. 问题简化：

• 忽略线路潮流不等式约束：即假设电力系统中的功率流动不受线路限制。在实际应用中，线路潮流的限制是非常重要的，但在这个简化模型中被忽略。
• 忽略网络损耗：假设没有损失，即没有电力在传输过程中因电阻、热等因素而消耗。这意味着所有的功率都会完全到达目标节点，这也是一个简化。
• 忽略发电机出力不等式约束：忽略发电机的最大输出和最小输出限制。在实际中，发电机的功率输出有上限和下限，在这个模型中，这些限制被简化掉了。

2. 数学模型简化：

• 目标函数：通过最小化总发电成本来进行优化。目标是使得总发电成本最小化。即：
  [
  \min , C_T = \sum_{i=1}^{m} C_i(P_{G_i})
  ]
  其中，( C_i(P_{G_i}) ) 是第i台发电机的成本函数，( P_{G_i} ) 是它的发电功率输出。

• 等式约束：总的功率输出必须等于负荷需求。即：
  [
  \sum_{i=1}^{m} P_{G_i} = P_D
  ]
  这个约束条件保证了电力系统的平衡，即发电机输出的总功率必须满足负荷的需求。

3. 潮流方程是否需要约束：

• 是否需要考虑潮流约束：提出了是否需要将潮流方程的约束纳入经济调度模型的讨论。潮流约束在实际系统中是非常重要的，因为它决定了功率如何在网络中流动，并影响到电力系统的稳定性和安全性。简化模型中没有考虑这些约束，但在复杂模型中，潮流约束是必须要考虑的。

总结：

这张图展示了一个简化的经济调度问题（ED）模型，重点忽略了电力系统中的一些关键约束（如潮流约束和损耗），目的是使问题更容易求解。通过最小化发电成本来求解优化问题，并确保电力平衡。这个模型对理解经济调度的基础非常有用，但在实际应用中，必须考虑更多复杂的约束条件以确保电力系统的稳定运行。

这张图展示了传统经济调度（ED）中等微增率（IC）准则的应用及其数学推导过程。以下是该内容的详细解读：

1. 等微增率准则的重要性

• 核心思想：如果在存在最优解的情况下，所有发电机的发电成本增加率（即等微增率，IC）应该是相等的。也就是说，在最优解下，每个发电机增加单位功率所增加的成本是相同的。
• 应用背景：这个准则非常关键，因为它帮助我们确保在经济调度中，所有发电机的运行成本变化（随发电量的增加）在最优解时保持一致。若每台发电机的增量成本不相等，就说明调度尚未优化，系统可能存在更优解。

2. 数学模型的构造

• 在经济调度问题中，我们需要构造一个拉格朗日乘子法（Lagrange Multiplier Method）来求解优化问题。首先构造L函数，它将目标函数（总成本）和约束条件（功率平衡）结合起来。目标是最小化总发电成本。

  [
  \min L = C_T = \sum_{i=1}^{m} C_i(P_{G_i}) - \lambda \left( \sum_{i=1}^{m} P_{G_i} - P_D \right)
  ]

  其中：

  • ( C_T ) 是总发电成本。
  • ( P_{G_i} ) 是第( i )个发电机的功率输出。
  • ( P_D ) 是系统的负荷需求。
  • ( \lambda ) 是拉格朗日乘子，用于确保功率平衡约束。

3. L函数的最优化

• 要求最小化L函数，需要对L函数进行求导并求解。为此，我们需要对每个发电机的输出功率进行偏导数操作，得到以下方程式：
  [
  \frac{\partial L}{\partial P_{G_i}} = \frac{\partial C_T}{\partial P_{G_i}} - \lambda = 0
  ]
  该方程表示的是最优解的条件，即每个发电机的增量成本等于拉格朗日乘子。

• 此外，还需要满足功率平衡条件，即总发电功率等于负荷需求：
  [
  \sum_{i=1}^{m} P_{G_i} = P_D
  ]

4. 结论

通过这些方程，我们可以求解得到每台发电机的最优出力，从而得到全系统的最优调度方案。等微增率准则帮助我们确保所有发电机的发电成本增加率在最优解时相等，这也是最优经济调度的关键准则之一。

总结

通过拉格朗日乘子法结合等微增率准则，优化问题能够有效地求解。在实际应用中，经济调度需要综合考虑多个发电机的运行成本与功率平衡，从而达到降低成本并满足负荷需求的目标。

这张图片进一步深入讨论了传统ED（经济调度）问题的等微增率（IC）准则，具体的数学推导如下：

1. 等微增率准则的数学表达

• 在传统经济调度问题中，目标是最小化总的发电成本，公式为：
  [
  \frac{dC_i}{dP_{G_i}} = \lambda \quad \text{(对于所有发电机i)}
  ]
  这里，(\frac{dC_i}{dP_{G_i}}) 表示发电机i的增量成本，即发电机i每增加单位功率所增加的成本。根据等微增率准则，所有发电机的增量成本应当相等，即等于拉格朗日乘子 (\lambda)。

  此外，必须满足功率平衡约束条件：
  [
  \sum_{i=1}^{m} P_{G_i} = P_D
  ]
  其中，(P_{G_i}) 是发电机i的发电功率，(P_D) 是系统的负荷需求。

2. 数学模型的解释

• 线性代数方程组：这表示了一个包含 (m+1) 个方程和 (m+1) 个待求量的线性系统。在这些方程中，我们既有未知的发电功率 (P_{G_i})，也有未知的拉格朗日乘子 (\lambda)，它在模型中起到调节各发电机增量成本的作用。
• 拉格朗日乘子 (\lambda)：它不仅代表了公共成本的微增率，也代表了系统总成本的微增率。在经济调度中，它是至关重要的，因为它帮助平衡每个发电机的成本与系统整体运行成本之间的关系。

3. 经济学术语

• 边际成本：在经济学中，(\lambda) 被称为边际成本。它是指每增加一单位发电量所带来的成本增加，表示系统最优运行时每个发电机的成本变化。根据等微增率准则，所有发电机的边际成本应当相等，从而达到成本最小化。

4. 问题的实际应用

• 已知负荷时的计算：当我们知道系统的负荷需求 (P_D) 时，可以使用上面的公式来计算所有发电机的最优发电功率 (P_{G_i})，以及最优的拉格朗日乘子 (\lambda)。
• 如何通过微增量变化调整成本：当负荷需求 (P_D) 发生微小变化时，如何通过调整各个发电机的发电功率，使得系统成本的变化最小，这是等微增率准则的核心问题。

5. 总结

等微增率准则是经济调度问题中的关键概念。它通过确保所有发电机的增量成本相等来实现发电系统的成本最小化。通过数学模型和拉格朗日乘子法，我们可以求解出最优的发电功率分配，进而达到经济运行的目标。

希望这有助于你理解传统经济调度问题中的等微增率准则及其应用！

这张图片展示了一个两机系统中的经济调度（ED）问题，具体探讨了如何通过调整发电机的运行点来实现等微增率准则。下面是详细解析：

1. 等微增率（IC）准则的图形表示

• 发电机1的增量成本 (C_1(P_{G1}))：显示了发电机1随其发电功率 (P_{G1}) 增加的成本曲线，增量成本为 (IC_1)。
• 发电机2的增量成本 (C_2(P_{G2}))：显示了发电机2随其发电功率 (P_{G2}) 增加的成本曲线，增量成本为 (IC_2)。
• 在最优调度条件下，增量成本 (IC_1) 应该等于 (IC_2)，因为这符合等微增率准则。

2. 反证法说明

• 假设：假设在某一情况下，发电机1 和 发电机2 的增量成本不相等，即 (IC_1 \neq IC_2)，并且假设 (IC_1 > IC_2)。
• 根据这种假设：
  • 如果减少 (P_{G1})，则成本节省为 ( \epsilon \times IC_1)（这是通过减少发电机1的输出，减少的成本）。
  • 同时，如果增加 (P_{G2})，则成本增加为 ( \epsilon \times IC_2)（这是通过增加发电机2的输出，增加的成本）。

3. 总结

• 在最优调度中，总发电量不变，但是通过改变发电机的运行点，减少发电机1的输出并增加发电机2的输出，这将会减少总成本。
• 总成本节省：( \epsilon \times (IC_1 - IC_2) > 0 )，这意味着通过调整发电机的运行点可以节省更多的成本。
• 结论：如果增量成本 (IC_1) 不等于 (IC_2)，那么原始的运行点就不是最优解，通过调整运行点，使得 (IC_1 = IC_2)，才能得到最优解。

4. 应用

这种分析方法可以帮助确定如何根据不同发电机的增量成本，优化其发电功率分配，从而达到最低的运行成本。这种策略在经济调度问题中非常常见，特别是在需要同时考虑多个发电机的情况下。

这张图片展示了一个2机系统的具体计算示例，用于经济调度（ED）问题的解决。我们通过使用等微增率（IC）准则来找到最优解。以下是详细的解析：

1. 问题描述

我们有一个2机系统，其发电成本函数分别为：

• (C_1(P_{G1}) = 9000 + 450P_{G1} + 0.1P_{G1}^2)（单位：￥/小时）
• (C_2(P_{G2}) = 25000 + 430P_{G2} + 0.03P_{G2}^2)（单位：￥/小时）

目标是满足总负荷 (P_D = 700) MW，且通过等微增率准则找到经济调度的最优解。

2. 计算增量成本（IC）

首先，计算发电机1和发电机2的增量成本（IC），即每个发电机的成本对发电功率的导数。

• 发电机1的增量成本：
  [
  IC_1 = \frac{dC_1}{dP_{G1}} = 450 + 0.2P_{G1}
  ]

• 发电机2的增量成本：
  [
  IC_2 = \frac{dC_2}{dP_{G2}} = 430 + 0.06P_{G2}
  ]

3. 应用等微增率准则

根据等微增率准则，发电机1和发电机2的增量成本（(IC_1) 和 (IC_2)）应该相等。

• 设定 (IC_1 = IC_2)，则：
  [
  450 + 0.2P_{G1} = 430 + 0.06P_{G2}
  ]

• 由于总负荷 (P_{G1} + P_{G2} = 700)，因此我们可以求解出 (P_{G1}) 和 (P_{G2})。

4. 计算解答

通过求解上述方程组，得到：

• (P_{G1} = 84.6) MW
• (P_{G2} = 615.4) MW

从而得出：

• (IC_1 = IC_2 = 466.9) ￥/MWh

5. 结果解释

• 根据等微增率准则，发电机2 应该比 发电机1 发电更多的电，这样可以使系统的总发电成本最小化。

6. 结论

此计算过程展示了如何通过等微增率准则优化发电机的出力，以实现最小化发电成本，并确保系统满足总负荷的需求。

这张图片提出了一个电力系统中的问题：

问题描述：

• 发电出力有上下限？
• 解不满足怎么办？

这个问题是关于电力系统调度中如何处理发电机的功率上下限约束的。在实际的经济调度（ED）问题中，发电机的出力通常有最大值和最小值的限制，这会影响发电机的调度和发电成本的优化。

处理方法：

1. 设置上下限约束：
   每个发电机的出力通常会有一个最小值和最大值。例如，某个发电机的出力可能限制在50 MW到300 MW之间。这个限制是由发电机的物理特性、效率和运行条件决定的。

2. 解不满足时的应对：
   如果计算的最优解不满足这些上下限条件，通常有以下几种处理方法：

   • 调整发电机出力： 将某些发电机的出力限制在其最大或最小功率范围内，并通过其他发电机的调节来满足总负荷需求。
   • 引入惩罚项： 在优化模型中加入惩罚项，对于不能满足的负荷增加额外的成本，以确保结果更符合实际操作要求。
   • 分配约束： 如果发电机的出力限制无法满足需求，可以考虑调整负荷分配或增加备用发电机的启动，以增加系统的灵活性。

3. 优化调整：
   在一些高级调度算法中，可能会使用更加复杂的数学模型（如拉格朗日乘子法或线性规划），来确保优化问题的约束条件被满足。

总结：

这个问题涉及到如何在电力系统中有效地管理发电机的输出，并确保系统在符合物理和技术约束的情况下运行，达到最优经济调度的目标。

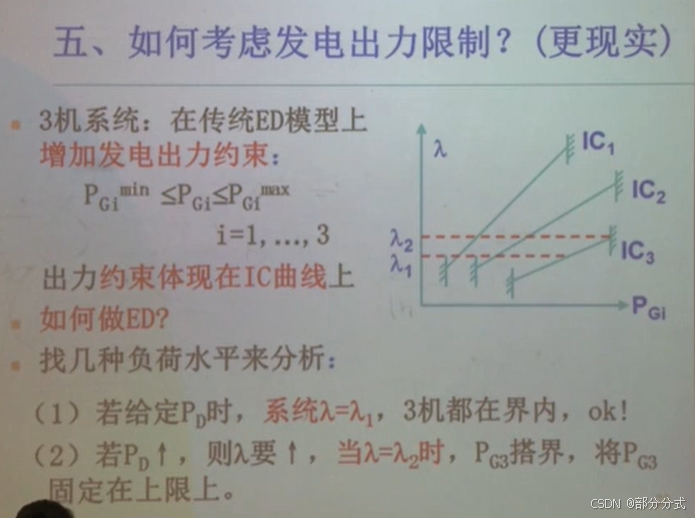
这张图片讲述了如何在电力调度中考虑发电机的输出限制，特别是在传统经济调度（ED）模型中，如何将发电机的输出功率限制加入到模型中。

问题描述：

• 在一个有3台机组的系统中，传统的经济调度（ED）模型已考虑了各机组的出力限制：
  [
  P_{Gi_{\min}} \leq P_{Gi} \leq P_{Gi_{\max}}
  ]
  其中，(P_{Gi_{\min}}) 和 (P_{Gi_{\max}}) 分别是机组的最小和最大出力。目标是找出如何在这些限制下进行经济调度。

• 然后，讨论了如何在加入这些约束条件（如功率的上下限）后，依然保证经济调度模型的有效性。

如何处理这些问题：

1. 出力约束与IC曲线：
   该图展示了IC（增量成本）曲线的变化。IC曲线用于表示随着出力增加，系统增量成本的变化。当约束条件被加入后，系统的增量成本可能出现不连续的变化，图中给出了不同出力下的IC曲线（(IC_1)，(IC_2)，(IC_3)）。

2. 增量成本与约束条件的关系：

   • 通过不同的增量成本（(IC_1)，(IC_2)，(IC_3)），可以调整系统的出力分配，以使整个电力系统的调度符合经济目标，并且满足发电机出力的上下限约束。
   • 当增加发电机的输出功率时，增量成本也会增加（根据具体的约束条件）。

3. 两种分析方式：

   • 若给定总负荷 (P_D) 时，(\lambda_1) 的值，可以确保系统中的所有机组都在其允许的功率范围内运行。
   • 若总负荷 (P_D) 已经给定，调整 (P_G) 时，系统的增量成本曲线将根据功率约束条件而变化。

结论：

• 当存在功率上限和下限时，优化模型需要根据每个机组的增量成本进行调整。
• 通过拉格朗日乘子法等优化工具，可以确保每台机组的出力在其允许范围内，并找到最低的总发电成本。

总的来说，这个问题探讨了在电力系统调度中如何平衡发电机的运行约束与经济调度的优化目标，确保在满足约束的前提下实现成本最小化。

这张图片讲述了如何在电力调度中考虑发电机的输出限制，并根据增加的负荷如何调整系统的出力和增量成本（IC）。

主要内容：

• 增量成本与负荷的关系：
  • 在电力调度中，增量成本（IC）随发电机出力 (P_{Gi}) 的增加而变化。该图展示了不同的增量成本曲线（IC1、IC2、IC3），反映了随着发电机出力的变化，系统增量成本的不同。

具体的操作步骤：

1. 若负荷 (P_D) 继续增加：

   • 系统的负荷增加时，发电机 (P_{G1}) 和 (P_{G2}) 必须承接更多的负荷。因此，这两台机组的增量成本 (IC) 必须保持相等，即 (\lambda_1 = \lambda_3)，确保两台机组在相同的增量成本下继续增加出力。

2. 若负荷继续增加：

   • 当负荷继续增加时，直到某个点，增量成本变为 (\lambda_4)，并且 (P_{G2}) 达到其最大限制。这时，增加的负荷只能由其他机组继续承担，而不再由 (P_{G2}) 承担。

3. 当负荷继续增加时，只有 (P_{G1}) 承担增加的负荷：

   • 当所有机组的输出已经达到最大输出限制时，增量成本趋于某一特定值，只能由 (P_{G1}) 承担所有剩余负荷的增加。

结论：

• 在考虑发电机的输出限制时，电力调度需要根据各机组的增量成本来决定负荷的分配。增量成本曲线 (IC) 的变化决定了负荷如何分配到各个机组中。
• 当系统负荷增加到一定程度时，某些机组可能会达到其最大输出限制，此时只能通过调整其他机组的输出或改变调度策略来满足负荷需求。

这张图的重点在于通过调整发电机的出力限制和增量成本，确保电力系统的负荷分配能够在经济调度的框架内实现，同时满足各机组的技术约束。

这张图片解释了如何在电力调度中考虑发电机的输出限制，并提出了适用于更一般电力系统调度（ED）的准则。

主要内容：

1. ED准则：

   • 在电力调度中，首先需要找到一个初始值，以确保所有机组的增量成本（IC）相等，并且满足负荷上的约束。这是电力系统调度中的一个基本准则。

2. 若无法满足负荷需求：

   • 如果负荷需求无法通过当前的发电机输出满足，则需要调整增量成本 (\lambda) 以进一步优化调度。在这种情况下，发电机的出力会逐步调整，直到满足负荷需求。

3. 发电不足与过剩：

   • 若发电机的发电不足，则调整 (\lambda)，使得输出增加到满足负荷需求的水平。
   • 若发电过剩，则需要降低 (\lambda) 来减少过剩的发电，避免浪费和不必要的成本。

4. 机组出力搭配：

   • 如果某些机组已经达到其最大输出限制（发电机出力达到上限），则在接下来的调度中，这些机组的增量成本将与其他机组继续平衡，直到满足负荷需求。

结论：

• 这些准则帮助电力调度人员在实际操作中，通过合理调整发电机出力和增量成本，确保电力系统能够在满足负荷需求的同时，以最低成本进行运作。
• 这也为如何应对负荷不满足的情况提供了指导：通过调整增量成本，系统能灵活响应变化的负荷需求。

应用场景：

• 反证法： 这部分提到的反证法主要用于验证上述调度方法的正确性。通过数学模型和推理，证明这些准则在实际应用中能够确保优化调度和负荷的平衡。

这张图片讨论了如何在电力系统调度中考虑网络损耗，并给出了相应的分析方法。

主要内容：

1. 如果发电机位于同一厂区或附近：

   • 这种情况在调度中可以直接忽略网络损耗，因为在这种情况下，发电机之间的连接比较直接，损耗相对较小。

2. 现代电力系统中的电厂分布和网络：

   • 由于现代电力系统中电厂的分布较为分散，考虑到电力网络的损耗是非常必要的。因此，传统的ED准则需要进行修正以考虑网络损耗。

3. 最简单的情况：

   • 在简单的情况下，如果系统中的所有机组都位于相同位置，则可以忽略网络损耗。在这种情况下，若考虑网络损耗，负荷中心越靠近发电机，电力的损耗就越小。

4. 更一般的情况：

   • 如果已知负荷 (P_D)，假设网络损耗为 (P_L(P_G))，则需要修正调度方案，并引入功率平衡的约束条件，公式如下：
     [
     \sum_{i=1}^{m} P_{Gi} - P_L(P_G) - P_D = 0
     ]
     这个公式表示系统中所有发电机的总输出减去网络损耗后的结果应等于负荷需求。

应用场景：

• 网络损耗的考虑： 在电力调度中，考虑电网损耗是非常重要的，尤其是在电厂分布广泛的情况下。忽略网络损耗可能导致不准确的成本计算和电力供应问题。

• 网络优化： 通过修正传统的ED模型，引入网络损耗的计算，可以更准确地预测电力系统的成本和性能，确保系统在满足负荷需求的同时，实现最优化的运行。

结论：

• 传统的电力系统调度模型通常忽略了网络损耗，但是随着电力网络的复杂化，修正后的模型能够更真实地反映系统的运行情况。在实际调度中，考虑网络损耗有助于提高电力系统的效率并减少不必要的成本。
  
  这张图片讨论了电力市场的改革及其对电力调度的影响，特别是关于电网的分开、市场竞争和成本最小化的问题。

主要内容：

1. 电力市场环境下的改革：

   • 电网分开：电力市场改革通常会导致电网与发电厂分开运营，电力公司从不同的电厂购买电力，并将电力提供给最终用户。这种分开有助于促进竞争，提高电力市场的效率。
   • 市场化交易：电力公司通过市场化的机制采购电力，意味着电力的生产和供应将更多依赖于市场的供需关系和价格信号，而不是由政府或单一电力公司控制。

2. 电网老板的目标：

   • 电网的管理方，或称电网“老板”，仍然追求在这种市场化环境下的最优调度，也就是发电成本最小化。这意味着，在电力市场竞争中，电网公司依然希望以最低的成本满足市场需求，从而确保电力系统的经济性和稳定性。

应用场景：

• 电力市场化：随着电力市场的改革，电网不再是垄断的主体，电力供应和需求更具市场化特征。在这种背景下，电力公司需要根据市场价格、需求等因素来决策，而不是依赖传统的定价模式。

• 成本最小化：尽管电网与发电厂分开，电网公司仍需要通过优化调度和购电策略来降低电力生产的整体成本，并尽量降低用户的电力费用。

结论：

• 电力市场改革促进了竞争和效率，但电网公司仍然有责任确保电力供应的经济性和可靠性。这意味着，电网公司依然需要追求发电成本最小化，以便满足市场需求并维持稳定的电力供应。