运筹优化入门---ChatGPT4o作答+Jang Stree：运筹优化科普与研究入门

这张图片提到了几个核心概念，涉及到运筹学、优化、以及与其相关的学科。以下是这些概念的详细解释：

1. Operations Research (运筹学)

运筹学（Operations Research, OR）是一门应用数学和统计学的学科，主要用于帮助决策者在复杂的系统中做出最优决策。运筹学通常结合数学建模、统计分析、计算机仿真等工具来解决实际问题。它广泛应用于各行各业，包括交通运输、供应链管理、生产调度、金融分析等。

• 运筹学的目标是通过优化模型，帮助决策者提高效率、节约成本或最大化利润。
• 运筹学的应用实例包括：
  • 运输问题：如何通过最短路径或最低成本将货物从多个仓库运送到多个目的地。
  • 生产调度问题：如何安排生产过程，使得资源使用最大化，同时尽量减少生产成本和时间。

2. Optimization (优化)

优化（Optimization）是运筹学的一个核心分支，指的是寻找在某些约束条件下，能使目标函数达到最优（最小或最大）值的过程。优化问题广泛存在于现实生活中，包括金融投资、资源分配、物流规划等。

• 优化的类型：
  • 线性优化：目标函数和约束都是线性的，常见的有线性规划（Linear Programming, LP）。
  • 整数优化：部分或全部变量是整数，常见的有整数规划（Integer Programming, IP）和混合整数规划（Mixed-Integer Programming, MIP）。
  • 非线性优化：目标函数或约束是非线性的，常见的有非线性规划（Nonlinear Programming, NLP）。

优化的目的是帮助找到一个在给定约束下最优的解，这个过程通常需要使用一些算法来求解，如单纯形法、内点法、分支限界法等。

3. 高级运筹学（高级优化）

高级运筹学/高级优化主要指对更复杂的优化问题进行深入分析，常涉及高维、大规模、非线性或者不确定性模型的优化。其应用涉及的领域包括：

• 大规模优化：处理大量变量和约束的优化问题。
• 组合优化：求解组合优化问题，如旅行商问题、背包问题等。
• 随机优化：处理在不确定性或随机条件下进行优化的情况，如库存管理、金融风险优化等。

这些高级优化技术通常要求更高的数学理论基础和更复杂的算法，例如拉格朗日乘数法、KKT条件、动态规划等。

4. 优化、最优化（Optimization, Maximization/Minimization）

这里提到的“优化”和“最优化”是优化学科的核心目标。具体来说：

• 最优化（Maximization/Minimization）意味着找到目标函数的最大值或最小值，通常是要使目标函数的值达到一个最优解。
  • 例如，在生产调度问题中，目标是最小化生产成本或者最大化生产效率。
  • 在投资组合优化中，目标是最大化投资回报或者最小化风险。

5. 运作管理、作业管理、管理科学

这一部分强调运筹学在管理科学中的重要性。管理科学（Management Science）是一种应用数学的科学方法，通常用于解决企业和组织中的决策问题，包括生产管理、资源分配、库存管理、运输与物流等。

• 运作管理：关注日常业务流程的有效管理和优化。例如，如何通过合理安排生产计划、库存控制和资源调度来提高企业运作效率。
• 作业管理：与企业日常运作中具体任务的调度和分配有关，如生产线作业调度、员工任务分配等。
• 管理科学：使用定量分析方法来支持管理决策。例如，如何通过数据分析和建模，帮助管理层作出更科学、更有效的决策。

总结

这张图片总结了优化和运筹学的核心内容，并强调了这些领域在管理、决策支持系统中的广泛应用。运筹学和优化通过建立数学模型并求解最优解，帮助各行各业提高资源利用效率、降低成本、增加盈利。

这张图片展示了“优化”在历史和应用领域的演变，尤其是与运筹学和优化相关的重要事件和发展。以下是对图片中内容的详细解读：

1. “优化”一直是生产生活中重要的部分

• 引用了莱昂哈德·欧拉（L. Euler）的名言：“Nothing at all takes place in the Universe in which some rules of maximum or minimum does not appear”（在宇宙中没有任何事情发生，而没有最大或最小的规则出现）。
• 这句话强调了优化在自然界和人类生活中的普遍性。无论是自然过程还是人工设计的系统，优化原则都在其中发挥着重要作用。

2. 20世纪40年代，现代运筹学起源于第二次世界大战（1939-1945）

• 运筹学在第二次世界大战期间得到了快速发展。使用数学模型来解决战时问题，如雷达的部署问题、飞机与长距离飞行器的调度问题以及物资储存问题。
• 标志性事件：
  • 1947年，George Dantzig 提出了单纯形法，这是一种经典的线性规划求解方法，被认为是20世纪最重要的算法之一。

3. 20世纪50-80年代，运筹学应用的扩展

• 二战后，运筹学迅速被应用到企业和政府管理中，涉及生产、服务、金融等多个领域。这个时期，数学优化方法开始深入到实际决策问题中。
• 例如，运筹学的应用主要集中在 整体规划问题，如最短路径问题、生产调度、库存管理等方面。
• 这一时期运筹学方法的快速发展，推动了诸如 线性规划、整数规划 等技术的应用。

4. 20世纪90年代，计算技术的高速发展

• 随着计算机技术和软件的不断进步，人们解决优化问题的能力不断增强，运筹学的应用也变得更加广泛。
• 软件的兴起：
  • Cplex 和 AMPL 等优化软件的出现，极大地提高了求解大规模优化问题的能力，使得更多企业和学术界能够利用这些工具来解决复杂的决策问题。

5. 21世纪，数据时代带来了新的挑战

• 随着大数据和人工智能的兴起，如何将大数据转化为优化决策成为运筹学的新挑战。这涉及到如何从大量数据中提取有效信息，并基于这些信息进行最优决策。
• 新课题：
  • 如何将数据分析与优化结合起来，实现更高效、更精确的决策过程。
  • 这一领域涵盖了数据科学、机器学习、人工智能与传统优化方法的结合，形成了更加复杂的优化模型和求解方法。

总结

这张图片的核心内容是运筹学和优化学科的发展历程，以及它们在不同历史时期的应用。优化技术的快速发展，尤其是计算机和软件工具的进步，使得我们能够在更复杂的环境中进行决策优化。随着大数据和AI技术的发展，如何将数据科学与传统优化方法结合，成为现代运筹学面临的新的重要课题。

这张图片进一步强调了“优化”和“运筹学”在决策中的核心作用，并给出了关于运筹学的定义和其应用领域。以下是图片中内容的详细解读：

1. “Science of better”

• 运筹学通常被称为“更好的科学”（Science of better）。这一说法表明，运筹学的核心目标是优化决策过程，使得资源的配置和利用达到更高的效率。通过运筹学方法，决策者能够基于数学模型和数据分析，找到最优或近似最优的解决方案。

2. “在给定资源约束下，合理调配资源进行量化决策，以实现设定目标尽可能优化”

• 这段话进一步解释了运筹学的核心任务——如何在有限的资源下，通过科学的调配与优化，达到最优或近似最优的决策结果。
• 资源约束：指的是有限的资金、时间、人员、设备等资源。
• 量化决策：指将问题转化为数学模型，通过数值化的方法进行决策分析。

3. 运筹学（Operations Research, OR）的定义

• 运筹学（Operations Research, OR）是研究如何为复杂的工程或管理问题构建数学模型，以及如何分析这些模型，进一步探索可能的解决方案的一门学科。
• 运筹学不仅仅是理论的，它强调如何将数学建模和分析方法应用于实际的决策问题，解决涉及资源配置、调度、优化等方面的问题。

4. 运筹学的定义中的关键词：

• 跨学科（interdisciplinary）：运筹学涉及到多个学科领域的知识，包括数学、计算机科学、经济学、管理学等。
• 基于科学的数据驱动策略/政策/决策（data-driven strategy/policy/decision）：强调运筹学不仅依赖于数学模型，还强调数据的使用，决策过程是通过分析大量数据来指导的。
• 复杂/不确定/动态环境（complex/uncertain/dynamic environments）：运筹学广泛应用于面对复杂和不确定环境的决策问题，解决实际系统中由于动态变化和不确定性带来的挑战。

5. 运筹学的目标和方法

• 运筹学的目标是通过合理的资源配置和决策优化，在不确定和动态环境下做出最佳决策。运筹学的方法包括数学建模、数据分析、模拟仿真等多种手段，用于指导和改进实际决策过程。

总结

这张图片中的内容深入探讨了运筹学的定义和应用，强调其在优化决策过程中的重要性。运筹学不仅仅是数学模型的应用，它是基于跨学科的科学方法，数据驱动的策略和决策制定方法，在面对复杂、不确定和动态环境时，能够帮助我们做出更好的决策。


这张图片进一步探讨了“优化”的基本概念，并通过一个图示简洁地展示了优化的过程和方法。以下是该图的详细解读：

1. 优化的定义

• 优化：指在满足约束条件的前提下，寻找使目标函数达到最大值或最小值的最优策略。优化的核心是如何在限制条件下做出最佳决策，通常目的是在某个特定目标上获得最好的结果。

2. 两个关键步骤

• 建模：
  • 将实际问题通过数学形式进行建模。建模的过程涉及把实际世界中的问题抽象成数学公式，明确决策变量、目标函数以及约束条件。
• 求解：
  • 使用有效的优化算法，通过数学模型进行求解，找到最优解。求解过程通过数学运算和计算机算法来实现，最终得到满足约束条件下的最优解。

3. 建模与求解者的不同

• 好的模型：确保数学模型能够准确地反映实际问题，并且能够通过合适的计算方法进行求解。
• 好的求解方法：在有了有效的数学模型后，选择合适的优化算法和求解方法进行求解。优化算法的选择非常关键，因为它决定了求解效率和准确性。

4. 运筹学的关键任务

运筹学的核心任务之一就是在建模和求解之间架起桥梁，设计出合适的数学模型并选择高效的算法来解决实际问题。优化模型的设计和求解方法的优化是运筹学的两大核心问题。

5. 优化过程的图示

图示展示了优化过程的一个简化版本：

• 实际问题 -> 优化模型 -> 求解。
• 优化模型包括三个主要部分：
  • 决策变量（变量）：优化过程中需要确定的量。
  • 目标函数：需要优化的函数，可能是最大化或者最小化的目标。
  • 约束条件：限制决策变量的条件，定义了问题的解空间。
• 求解：优化算法用来求解数学模型并找到最优解。

总结

这张图片的内容强调了优化过程中的两个关键步骤：建模和求解。它还展示了如何将实际问题转化为数学模型，并使用合适的优化算法进行求解。运筹学的核心任务是设计适当的模型并选择高效的算法，从而在复杂的决策问题中找到最优解。

这张图片展示了不同类型的优化模型，包括线性模型、线性整数模型和非线性模型，并通过具体的数学模型和图示解释了这些模型的应用。以下是对图片内容的详细解读：

1. 建模（Modelling）

• 线性模型（Linear model）：线性模型是优化问题中最常见的一种模型，目标函数和约束条件都是线性的。线性优化问题可以通过一些经典的算法（如单纯形法）进行求解。

• 线性整数模型（Linear integer model）：这种模型是线性模型的一个扩展，其中某些决策变量被限制为整数。常见的优化问题如“运输问题”和“背包问题”就属于线性整数规划。

• 非线性模型（Nonlinear model）：与线性模型不同，非线性模型中的目标函数或约束条件至少有一项是非线性的。求解非线性优化问题通常比线性问题更复杂。

2. 具体的数学模型示例

• 线性规划示例：

  • 目标：最小化 ( x_1 - 2x_2 )
  • 约束条件：
    • ( x_1 + x_2 \leq 40 )
    • ( 2x_1 + x_2 \leq 60 )
    • ( x_1, x_2 \geq 0 )

  这个数学模型的目标是通过优化决策变量 ( x_1 ) 和 ( x_2 )，在满足约束条件的情况下使目标函数 ( x_1 - 2x_2 ) 最小化。图中的灰色区域代表了可行解的域，所有满足约束条件的解都在该区域内。

3. 图示解释

• 图示（左图）：

  • 图中的区域 ( P ) 表示一个线性规划问题的可行域。在这个区域内的所有点（解）都满足约束条件。
  • 通过图形化的方法可以直观地看到，最优解（例如在图中可能标记为某个点）通常位于该可行区域的边界上。

• 混合整数规划（Mixed integer programming, MIP）示例（右图）：

  • 目标：最大化 ( 3x + 2y )
  • 约束条件：
    • ( 4x + 2y \leq 15 )
    • ( x + y \leq 8 )
    • ( x + y \leq 5 )
    • ( x \geq 0 )
    • ( y \geq 0 ) 且 ( y ) 为整数

  这是一个混合整数线性规划（MIP）问题，其中 ( x ) 是连续变量，( y ) 是整数变量。图中展示了不同解的结果，包括整数解（橙色曲线）和线性规划解（蓝色曲线），以及最优解。

4. 不同解的优化结果

• 优化解（Optimal IP solution）：最优整数规划解，即整数变量 ( x = 2 ) 和 ( y = 3 )，目标函数值为 12。
• 最优线性规划解（Optimal LP solution）：线性规划求解的最优解，得到 ( x = 2.5 ) 和 ( y = 2.5 )，目标函数值为 12.5。
• 最优混合整数规划解（Optimal MIP solution）：最优的混合整数规划解，得到 ( x = 2.75 ) 和 ( y = 2 )，目标函数值为 12.25。

总结

这张图片通过具体的数学模型和图示解释了不同类型的优化问题：线性模型、线性整数模型和混合整数模型。它展示了如何通过建模和求解优化问题来获得最优解，并通过图形化的方式帮助我们理解这些问题的求解过程。在实际应用中，这些优化模型广泛应用于供应链管理、生产调度、财务决策等领域。

混合整数规划（Mixed-Integer Programming, MIP）是线性规划（LP）的一种扩展，其中问题的决策变量既包括连续变量，也包括整数变量。混合整数规划广泛应用于各类实际优化问题，尤其是在工业工程、物流、金融、生产调度等领域。

1. MIP的基本概念

• 线性规划（LP）：线性规划的目标是最大化或最小化线性目标函数，约束条件也是线性的。所有的决策变量都是连续的。常见的求解方法包括单纯形法和内点法。
• 整数规划（IP）：整数规划的目标是最大化或最小化线性目标函数，但所有决策变量都被限制为整数。例如，在一个调度问题中，决策变量可能代表生产的机器数量或运输的货物数量，这些数量通常是整数。
• 混合整数规划（MIP）：混合整数规划结合了线性规划和整数规划的特点，其中一些决策变量是连续的，而其他变量是整数。MIP 问题通常用于那些需要整数决策的优化问题，如项目调度、物流配送、资源分配等。

2. MIP的数学模型

混合整数规划问题的标准形式如下：

目标函数：

[ \text{maximize/minimize} , c_1 x_1 + c_2 x_2 + \cdots + c_n x_n ]

约束条件：

[
\begin{aligned}
a_{11} x_1 + a_{12} x_2 + \cdots + a_{1n} x_n & \leq b_1 \
a_{21} x_1 + a_{22} x_2 + \cdots + a_{2n} x_n & \leq b_2 \
\vdots \
a_{m1} x_1 + a_{m2} x_2 + \cdots + a_{mn} x_n & \leq b_m \
\end{aligned}
]

变量类型：

• 连续变量：( x_1, x_2, \dots, x_p )（这些变量可以取任意实数值）。
• 整数变量：( x_{p+1}, x_{p+2}, \dots, x_n )（这些变量必须是整数）。
• 可以存在一些二进制变量：( x_i \in {0, 1} )（这些变量通常用来表示是/否决策，如开关、设施选择等）。

示例：

假设一个典型的混合整数规划问题如下：

目标函数：最大化利润

[
\text{maximize} , 3x_1 + 2x_2
]

约束条件：
[
\begin{aligned}
4x_1 + 2x_2 & \leq 15 \
x_1 + x_2 & \leq 8 \
x_1 + x_2 & \leq 5 \
x_1 & \geq 0 \
x_2 & \geq 0 \
x_1 & \text{integer} \
x_2 & \text{binary} \
\end{aligned}
]

这个问题中，( x_1 ) 是整数变量（例如生产数量），而 ( x_2 ) 是二进制变量（例如是否开设一个仓库）。

3. MIP的应用场景

混合整数规划在许多领域中都有广泛的应用，尤其在那些需要决策部分为整数或二进制的实际问题中。以下是一些常见的应用场景：

3.1 生产调度与资源分配

• 生产计划：确定在给定的生产约束下，生产各类商品的数量，以最大化收益。
• 资源调度：例如，给定资源（如机器、员工等）的数量，如何安排工作任务以实现资源的最佳利用。
• 工厂布局：如何将不同的生产线、设备和仓库安排在一个工厂中，以降低运输成本并提高效率。

3.2 物流与运输

• 运输问题：优化货物从多个仓库运输到多个目的地的运输路径，同时最小化运输成本。
• 车辆路径规划：如何规划运输车辆的路径，使得所有配送任务在最短的时间内完成，并满足约束（如车辆容量、工作时间等）。

3.3 金融与投资组合优化

• 投资组合优化：确定投资的资金分配，以最大化投资回报，同时满足一些投资限制条件（如风险、流动性等）。
• 资本预算问题：在给定预算的情况下，选择哪些项目进行投资，以最大化投资收益。

3.4 供应链管理

• 设施选址问题：如何在多个候选地点中选择最佳的设施位置，以便最大化整体效益，通常包括物流成本、土地成本、运输时间等因素。
• 库存管理：如何确定库存水平，使得总库存成本最小，同时满足需求。

4. 求解MIP问题

求解混合整数规划问题通常比纯粹的线性规划问题更为复杂。常见的求解方法包括：

4.1 分支限界法（Branch and Bound）

• 这是求解混合整数规划问题最常用的方法之一。该方法通过将问题的解空间递归地分成多个子问题（分支），并利用界限（如目标函数值的上界或下界）来裁剪不可能包含最优解的子问题（限界），逐步缩小搜索范围，直到找到最优解。
• 分支限界法的效率较低，因此通常结合启发式方法来加速求解过程。

4.2 割平面法（Cutting Planes）

• 割平面法通过引入额外的约束（割平面）来逼近最优解。这些割平面可以切割掉部分不可行的解，从而提高求解效率。

4.3 启发式算法与元启发式算法

• 在实际应用中，许多MIP问题规模庞大，完全求解可能非常耗时。因此，启发式算法（如模拟退火、遗传算法、粒子群优化等）常被用于寻找近似最优解。

4.4 商业优化求解器

• 如 CPLEX、Gurobi 和 XPRESS 等商业优化求解器可以非常高效地解决混合整数规划问题，这些工具通常采用分支限界法、割平面法等技术，同时提供了强大的并行计算能力来加速求解过程。

5. MIP的挑战

• 计算复杂度：MIP问题的求解一般是NP-hard的，因此随着问题规模的增大，求解时间呈指数级增长。
• 精度问题：由于MIP的求解需要遍历大量的子问题，可能会出现精度误差，特别是在大规模问题中。
• 整数变量的复杂性：整数决策变量使得问题的解空间更加复杂，导致求解过程中的分支数和计算量大幅增加。

总结

混合整数规划是一个非常强大且灵活的优化工具，广泛应用于那些需要整数决策的实际问题。尽管求解这类问题通常非常复杂，但随着算法的改进和计算能力的提升，MIP已经成为求解许多复杂决策问题的标准工具。

这张图片展示了一个 非线性优化问题，其中包括了一个三维图形、数学模型以及约束条件。以下是详细分析：

1. 优化问题描述

优化问题的目标是最大化目标函数 ( p(x_1, x_2) )，该函数是一个由多个部分构成的非线性函数。目标函数的形式如下：

[
\text{max} , p(x_1, x_2) = \frac{60}{1 + (x_1 + 1)^2 + (x_2 - 3)^2} + \frac{20}{1 + (x_1 - 1)^2 + (x_2 - 3)^2} + \frac{30}{1 + (x_1)^2 + (x_2 + 4)^2}
]

其中，目标函数包含三个部分，每一部分都涉及到 ( x_1 ) 和 ( x_2 )，并且都是关于这两个变量的 非线性 项。

2. 约束条件

优化问题还包括以下约束条件：

[
(x_1 + 1)^2 + (x_2 - 3)^2 \geq \frac{1}{4}
]
[
(x_1 - 1)^2 + (x_2 - 3)^2 \geq \frac{1}{4}
]
[
(x_1)^2 + (x_2 + 4)^2 \geq 4
]

这些约束条件限制了 ( x_1 ) 和 ( x_2 ) 的值，确保优化的解满足特定的区域。

3. 三维图形

图中显示了一个三维表面图，表示的是目标函数 ( p(x_1, x_2) ) 随着 ( x_1 ) 和 ( x_2 ) 变化的变化情况。可以看到，目标函数有多个局部极值点（峰值），并且随着变量的变化，目标函数的值也会变化。

• 图中展示了目标函数的 波动形态，呈现出多个局部峰值，表明该问题具有 多重局部最优解，这也表明求解该问题可能面临局部极值的挑战。
• 这些图形帮助我们直观地理解该优化问题的形态，以及如何在这些峰值和谷值之间寻找全局最优解。

4. 解的候选点

图片中还标出了几个可能的解候选点，例如：

• ((-1, 3))
• ((1, 3))
• ((0, 4))

这些点可能是潜在的局部最优解，或者在实际求解过程中需要进一步验证的解。对于非线性优化问题，通常需要利用合适的算法（如梯度下降法、遗传算法、模拟退火等）来确定全局最优解。

5. 非线性优化的挑战

• 多峰问题：正如图形所示，目标函数有多个局部极值，这使得非线性优化问题比线性问题更为复杂。优化算法可能会陷入局部最优解，因此需要采取特殊的策略来寻找全局最优解。
• 算法选择：对于这样的非线性问题，常用的求解算法包括：
  • 梯度下降法：适用于连续且可微的目标函数，但容易陷入局部极值。
  • 遗传算法、粒子群优化等元启发式算法：这些方法不依赖于目标函数的连续性或可微性，可以有效处理具有多个局部最优解的复杂问题。

总结

这张图片展示了一个非线性优化问题，并通过数学公式、约束条件和三维图形阐述了问题的复杂性。目标函数包含多个非线性项，求解此类问题通常面临局部最优解的挑战。合适的优化算法和策略对于解决这类问题至关重要。

这张图片介绍了不同类型的优化算法，特别是求解线性规划（LP）、整数规划（IP）和非线性规划（NLP）问题时使用的精确算法。以下是图片内容的详细解读：

1. 优化算法的种类

1.1 线性规划（LP）

线性规划（Linear Programming, LP）是一个经典的优化问题类型，其目标函数和约束条件都是线性的。求解LP问题时，常用的精确算法包括：

• 单纯形法（Simplex method）：单纯形法是一种广泛使用的线性规划算法。它通过在可行域的顶点之间移动，逐步逼近最优解，通常效率较高，适用于中小规模的线性规划问题。
• 内点法（Interior Point method）：内点法是一种基于从内部进入可行域的思想的求解方法。与单纯形法不同，它通过沿着路径的方向从内部移动来寻求最优解。内点法通常适用于大规模线性规划问题。

1.2 整数规划（IP）

整数规划（Integer Programming, IP）问题是线性规划的一种扩展，其中某些决策变量被限制为整数。求解整数规划问题时，常用的精确算法包括：

• 分支限界法（Branch and Bound, B&B）：该方法通过递归地分解问题，利用界限（上界或下界）来裁剪掉不可能含有最优解的子问题，从而有效地减少搜索空间。
• 分支定界法（Branch and Cut, B&C）：这是分支限界法与割平面法的结合，适用于整数规划和混合整数规划问题。
• 分支与切割法（Branch and Price, B&P）：这种方法结合了分支限界法和价格算法，适用于有大量变量的整数规划问题。

1.3 非线性规划（NLP）

非线性规划（Nonlinear Programming, NLP）是优化问题中一种复杂的类型，目标函数或约束条件至少有一项是非线性的。求解非线性规划问题时，常用的精确算法包括：

• 梯度法（Gradient method）：梯度法是一种优化方法，通过沿着目标函数梯度的方向逐步更新决策变量，逼近最优解。它适用于连续且可微的优化问题。
• 拉格朗日松弛法（Lagrangian relaxation method）：拉格朗日松弛法将原始问题的约束条件部分松弛，通过引入拉格朗日乘子，将问题转化为更容易求解的形式，适用于一些特殊的非线性优化问题。

2. 三维图示与等高线图

图片中的三个图分别展示了优化问题的图形化表示，帮助理解不同算法如何工作。

• 左侧的三维图：该图展示了一个非线性目标函数在二维空间中的表现。图中的山峰表示目标函数的局部最大值，图中的不同区域代表不同的函数值。对于非线性优化问题，找到全局最优解（位于最高点）往往是一个挑战，因为局部最优解（局部峰值）可能误导算法。

• 中间的三维图：展示了另一个优化问题的三维函数表面，其中显示了多个局部极值点。此图的形态帮助我们理解非线性优化问题的复杂性，尤其是在多峰问题中，如何避免陷入局部最优解。

• 右侧的等高线图：这是一个常见的图形表示方法，展示了优化问题的等高线图（contour plot），其中每条线表示目标函数的相同值。等高线图有助于直观地理解目标函数的形态，尤其在使用梯度下降法等优化算法时，帮助我们理解最优化的方向。

3. 总结

这张图片深入介绍了求解线性规划、整数规划和非线性规划问题的精确算法。每种算法都有其适用的场景和优缺点：

• 对于线性问题，单纯形法和内点法是最常用的选择。
• 对于整数问题，分支限界法和分支定界法是最常见的解决方法。
• 对于非线性问题，梯度法和拉格朗日松弛法是常用的优化方法。

理解这些算法的原理和应用场景，有助于我们选择合适的求解方法，解决实际优化问题。

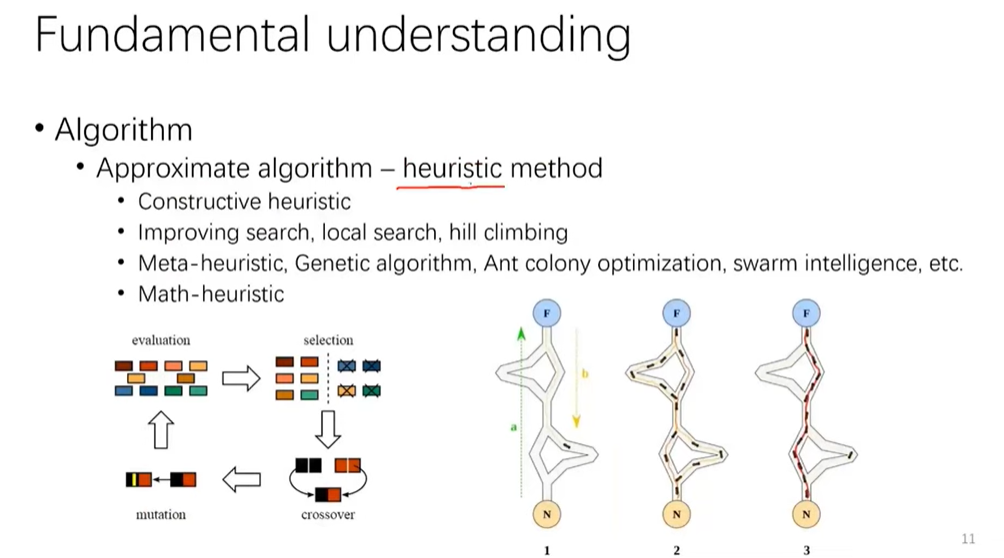
这张图片展示了启发式算法（Heuristic Algorithm）在优化问题中的应用。启发式算法是一类通过经验法则来寻找解决方案的算法，通常用于复杂的优化问题，特别是在解决大规模和复杂问题时，无法通过精确算法得到最优解时，启发式算法提供了一种近似解决方案。以下是对图片内容的详细解析：

1. 启发式算法（Heuristic method）

启发式算法是一类近似算法，用于寻找优化问题的解，通常不一定能找到全局最优解，但能够快速找到一个足够好的解。启发式算法在很多情况下比精确算法更有效，特别是当问题规模过大或计算资源有限时。

1.1 构造启发式算法（Constructive heuristic）

• 构造启发式算法通过逐步构建解决方案，通常从一个初始解开始，然后逐步添加部分解或改进现有解，直到满足一定的约束条件。
• 这类方法通常在没有明确目标函数的情况下，利用经验法则来快速构建一个可行解。

1.2 改进搜索（Improving search）

• 局部搜索（Local search）：局部搜索通过从当前解出发，搜索其邻域中的解，逐步改进解。常见的局部搜索方法包括“爬山法”（Hill climbing），通过在邻域中选择最优解并不断迭代，直到没有更好的解为止。
• 爬山法（Hill climbing）：爬山法是局部搜索的一种，类似于在山地中向上攀登，寻找局部最优解。该方法对于单峰问题有效，但在多峰问题中可能陷入局部最优解。

1.3 元启发式算法（Meta-heuristic）

• 遗传算法（Genetic algorithm, GA）：遗传算法模拟自然选择过程，通过选择、交叉、变异等过程，逐步优化解。它适用于大规模复杂问题，尤其是需要全局搜索时。
• 蚁群优化（Ant colony optimization, ACO）：蚁群算法通过模拟蚂蚁觅食的行为来寻找最优路径，尤其适用于路径规划和调度问题。
• 群体智能（Swarm intelligence）：群体智能是一类模拟自然界群体行为的优化算法，常见的如粒子群优化（PSO）。这些算法通过模拟群体的协同工作来寻找最优解。

1.4 数学启发式（Math-heuristic）

• 数学启发式方法结合了数学模型和启发式策略，通过数值优化和理论分析来指导搜索过程。它们往往依赖于问题的数学结构来引导搜索。

2. 算法流程图

图片展示了遗传算法的工作流程。遗传算法模拟了生物遗传过程，通常包括以下几个步骤：

• 评估（Evaluation）：计算每个个体（解）的适应度，适应度反映了个体在当前环境中的优劣。
• 选择（Selection）：根据适应度选择个体进行交配。适应度较高的个体被选中的概率较大。
• 变异（Mutation）：通过随机改变个体的基因（决策变量），以增加多样性并避免陷入局部最优解。
• 交叉（Crossover）：将两个个体的部分基因交换，产生新的个体，模拟基因的交换和组合，增加解的多样性。
• 下一代（Next Generation）：通过评估、选择、变异和交叉生成新一代的解。

3. 启发式算法的优缺点

• 优点：

  • 计算速度快：启发式算法通常不需要穷举所有可能的解，能够在合理时间内得到较好的解。
  • 灵活性强：可以根据问题的特点调整算法，以适应不同类型的优化问题。
  • 适用于大规模问题：对于大规模或复杂的问题，启发式算法能有效减少计算复杂度。

• 缺点：

  • 无法保证最优解：启发式算法通常无法保证找到全局最优解，而是得到一个足够好的解。
  • 依赖于初始解：有些启发式算法，如局部搜索，可能会受到初始解的影响，容易陷入局部最优解。

4. 总结

启发式算法在优化领域非常重要，尤其是在解决那些不能通过精确算法有效求解的复杂问题时。通过模拟自然过程、随机化搜索或通过局部搜索策略，启发式算法能够提供高效的解，尤其是在大规模问题或多峰问题中，常常能够找到足够好的解。

这张图片展示了管理问题与工程问题在实际应用中的不同领域及其联系，尤其强调了运筹学、管理科学以及优化技术在商业和工程领域中的广泛应用。

1. 管理问题

管理问题包括了运筹学（Operations Research, OR）、运营管理（Operations Management, OM）和管理科学（Management Science, MS）等领域，通常涉及如何通过优化、决策支持系统和资源管理来提高效率、降低成本，并实现最优运营。

• 商业（Business）：优化技术广泛应用于商业决策中，例如如何进行库存管理、资源配置、供应链管理等。目标是提升企业运作效率，最大化利润或优化生产过程。

应用场景：

• 库存管理：包括库存预定、补货、缺货问题等，确保库存水平保持在一个合理范围。
• 仓库管理：管理仓库中的存储空间、货物分类与调度等，优化存储与取货过程。
• 销售管理：包括产品的定价策略、促销策略以及产品的销售决策等。
• 物流与配送：如配送路径规划、运输资源调度等问题，确保物流系统的高效运行。
• 呼叫中心优化：通过优化人力资源和分配，提高服务效率和客户满意度。

2. 工程问题

工程问题通常涉及产品设计、生产和制造过程的优化。目标是提高产品质量、生产效率和降低生产成本。

• 工程（Engineering）：工程问题通常涉及到产品的设计、质量控制以及工艺流程优化等。优化技术可帮助解决如何在给定资源下，以最小的成本完成工程项目。
• 生产（Production）：生产优化问题涉及如何合理安排生产任务、生产线调度、资源分配等，目标是提高生产效率、减少浪费。
• 制造（Manufacturing）：制造问题集中在如何通过自动化、智能化设备与技术来提高生产效率与精度，确保产品质量并满足生产要求。

应用场景：

• 生产计划：如何高效安排生产线的工作流程，确保按时交付且降低生产成本。
• 质量控制：如何进行生产过程的监控，确保产品质量在规定标准内。
• 设施布局优化：如何合理布局生产设施，以便最大化效率和最小化物流成本。

3. 实际应用示例

• 库存与仓库管理：例如，如何通过优化库存管理来减少库存成本，同时确保产品能够及时交付。图中展示了一个仓库环境，如何根据需求进行库存补充和管理。
• 配送与物流问题：通过优化运输路线和区域划分来降低配送成本。图中展示了配送员按最优路径配送包裹。
• 呼叫中心优化：通过优化客户服务系统中人员的安排与工作流，提升响应效率，减少客户等待时间。

4. 总结

这张图片通过对管理问题与工程问题的不同应用场景分析，展示了运筹学、管理科学和优化技术在商业与工程领域的多样化应用。这些技术帮助企业和工程公司更好地管理资源、优化流程、提高生产率、降低成本，从而实现最优决策和提升竞争力。

这张图片展示了旅行商问题（TSP）和车辆路径问题（VRP），以及它们在实际应用中的不同表现和挑战。这两个问题都是典型的组合优化问题，并且广泛应用于物流、配送、运输等领域。

1. 旅行商问题（TSP）

旅行商问题（Traveling Salesman Problem, TSP）是一个经典的组合优化问题，目标是要求旅行商从一个起点出发，访问每个给定的城市一次，并且最后回到起点，要求路径最短。TSP是一个NP难题，难度随着城市数量的增加而急剧上升。

特点：

• 目标是找到一条经过所有城市的最短路径。
• 经典的旅行商问题是一个单一的路径，只有一个旅行商和一条路线。
• 图中的蓝色路径展示了TSP问题中的城市访问顺序。

2. 车辆路径问题（VRP）

车辆路径问题（Vehicle Routing Problem, VRP）是一类与TSP相关但更加复杂的问题。VRP不仅需要找到多个路径来覆盖多个地点，而且通常还包括多个限制条件，如车辆容量限制、时间窗等。

特点：

• 多个旅行商：在VRP中，我们有多个车辆（旅行商），而不是仅仅一个。
• 时间窗：每个配送任务有指定的时间窗，要求车辆在规定时间内到达。
• 容量限制：每辆车有一定的载货能力，不能超载。
• 图中的蓝色路径展示了多辆车分别执行配送任务的情况。

3. 实际问题中的挑战

图中的几个问题因素列出了TSP和VRP在实际应用中可能遇到的挑战：

1. 多个载体（Multiple carriers）：即存在多个车辆（卡车）和多个出发点。对于VRP，问题不仅仅是找到最短路径，还要合理安排每辆车的行驶路线，避免重复行驶，最大化效率。

2. 实际需求（Real-world demands）：在现实中，用户需求会随时间变化，因此必须采用适应性（adaptive）解决方法。即不断根据需求变化调整路径安排。

3. 时间窗（Time windows）：某些物品需要在特定时间内进行配送，或者需要满足客户的时间要求。如何在规定的时间内完成配送是一个重要挑战。

4. 承载限制（Capacity constraints）：每辆车的承载能力有限，因此如何合理安排每辆车的配送任务，避免超载，是解决VRP时需要考虑的重要因素。

5. 路况不确定性（Uncertainty in routes and delivery）：由于交通状况、天气等因素的变化，实际路径的时间和距离可能发生变化，因此路径规划必须考虑不确定性。

4. 总结

旅行商问题和车辆路径问题在现实生活中有广泛的应用，尤其在物流、配送和运输领域。它们在求解过程中面临的挑战主要来自于多个载体、动态需求、时间窗限制、容量限制和不确定性等因素。随着问题复杂性的增加，传统的精确算法往往无法在合理时间内求解，因此启发式算法、元启发式算法（如遗传算法、蚁群算法等）和混合整数规划（MIP）等方法成为了解决这些问题的重要手段。

这张图片强调了**优化（Optimization）**在现实生活中无处不在的广泛应用，展示了不同领域中优化技术的重要性。优化不仅仅是一个理论上的概念，它在许多实际应用中扮演着重要角色。

1. 优化在各个领域的应用

• 课堂教学（Education）：在教育领域，优化可以帮助管理课堂时间、安排课程内容、优化学生的学习进度和教学资源的分配。例如，如何通过优化教学计划，使得学生能够在有限的时间内获得最好的学习效果。

• 医疗健康（Healthcare）：在医疗领域，优化用于诊断和治疗的过程中。例如，通过优化诊断过程或治疗计划，医生可以根据患者的个体差异，找到最适合的治疗方案，提高治疗效果，并减少不必要的成本和时间浪费。

• 电力网络（Electricity network）：在电力网络中，优化技术被用来调度电力供应和需求。如何根据电网的负载情况和电力供应的可用性优化电力流向，以确保电网的稳定性和高效运行。

• 交通与路径规划（Transportation and Route Planning）：在交通领域，优化算法可以用来解决路径规划问题。例如，如何规划最短路径、最节省时间的路径，或者如何为城市交通流量设计最优的交通网络，提升出行效率并减少交通拥堵。

• 足球（Football）：在体育运动中，优化也非常重要。例如，如何优化球队的阵容配置、比赛策略和训练计划，以提高球队的整体表现。

• 生产和制造（Production and Manufacturing）：在制造业中，优化可以帮助提高生产效率、降低成本。通过优化生产线的安排、资源调度和库存管理，能够在保证产品质量的同时减少生产时间和资源浪费。

2. 总结

这张图片清晰地表明，优化不仅仅是数学和计算机科学中的一个抽象概念，而是一个在各个实际领域都非常重要的工具。无论是教育、医疗、能源、交通、体育还是生产领域，优化技术都可以帮助我们在有限资源的情况下做出最佳决策，从而提高效率、降低成本、提升效果。优化的应用几乎涵盖了我们的日常生活，并对社会的各个方面产生了深远的影响。

这张图片展示了**机器学习（Machine Learning）**在现实生活中的广泛应用以及机器学习的基本概念。

1. 机器学习的应用场景

• 垃圾邮件过滤（Spam Filtering）：机器学习可以帮助自动识别和过滤电子邮件中的垃圾邮件。通过训练模型，识别哪些邮件是垃圾邮件，哪些是正常邮件。

• 面部识别（Facial Recognition）：面部识别技术广泛应用于安防、智能手机解锁、支付验证等领域。机器学习可以通过分析人脸特征来进行身份识别。

• 视频推荐（Video Recommendation）：像Netflix这样的流媒体平台通过机器学习技术分析用户观看的历史记录，推荐可能感兴趣的内容。例如，《House of Cards》是Netflix平台根据用户兴趣推荐的视频内容之一。

• 自动驾驶（Self-Driving Cars）：自动驾驶技术利用机器学习来分析周围环境，做出行驶决策，确保汽车的安全与高效行驶。

• 智能语音助手（Voice Assistants）：例如亚马逊的Echo设备，使用机器学习来理解语音命令并执行任务（如播放音乐、控制智能家居设备、查询天气等）。

2. 机器学习的定义与类型

右侧的部分介绍了什么是机器学习，以及它的几种主要类型：

2.1 监督学习（Supervised Learning）

• 分类（Classification）：在监督学习中，分类问题指的是将数据点分配到预定义的类别中。例如，垃圾邮件检测将邮件分为“垃圾邮件”和“非垃圾邮件”两类。
• 回归（Regression）：回归问题是预测一个连续值的任务。例如，预测房价、股票价格等。

2.2 无监督学习（Unsupervised Learning）

• 聚类（Clustering）：在无监督学习中，聚类算法将数据点分为不同的组或簇，每个簇内的数据点具有相似性，而不同簇之间具有显著的差异。常用于客户分群、市场细分等场景。

3. 机器学习的重要性

机器学习无处不在，它在我们日常生活的各个方面扮演着重要角色。从邮件分类到自动驾驶，从视频推荐到语音助手，机器学习都在帮助我们提升效率和体验。随着数据量的不断增加和计算能力的提升，机器学习的应用领域也在不断扩展，成为了许多行业的核心技术。

4. 总结

机器学习不仅是一项先进的技术，它在实际生活中应用广泛，涉及从互联网到医疗、交通等多个领域。无论是通过监督学习进行分类和回归任务，还是通过无监督学习进行聚类，机器学习技术都为解决复杂问题提供了强大的工具和方法。

这张图片展示了优化和**机器学习（ML）**结合的前景，并引用了Dimitris Bertsimas的观点，强调数据在优化中的重要角色。

1. INFORMS新期刊：优化

• Dimitris Bertsimas的观点：他提到“优化领域中最大的机会之一是将数据作为主角并与机器学习结合。” 这句话表达了数据驱动优化和机器学习的潜力，意味着在未来的优化问题中，数据不仅仅是支持工具，而是优化过程的核心要素之一。

2. 优化的未来愿景

• 图片中的第二段文字展示了作者对优化未来的愿景。优化不再是仅仅依赖传统数学模型的过程，而是要结合数据分析、机器学习以及决策制定。
• 数据（Data）：数据是所有分析和模型构建的基础。通过大量的数据，可以识别出潜在的模式或趋势，为后续的模型和决策提供支持。
• 模型（Models）：模型是通过分析数据并构建的数学或统计模型，用来模拟实际问题的行为或决策。
• 决策（Decisions）：基于模型的输出，做出实际的决策。例如，在物流优化中，基于预测的需求数据做出运输调度决策。
• 预测（Predictions）：机器学习通过对数据的分析进行预测，帮助模型和决策过程更加精准。

3. 机器学习与优化结合

• 机器学习（ML）：机器学习被纳入到优化过程中，意味着通过模型训练不断改进优化策略。机器学习可以帮助优化模型从历史数据中学习，不断提高决策的准确性和效率。
• 优化（OR/Optimization）：传统的优化方法通过数学模型求解最优解，而现代的优化方法开始结合机器学习，以适应动态和复杂的现实世界问题。

4. 数据、模型和决策的互动

• 图片中的圆形图表展示了数据、模型和决策之间的互动关系。数据是优化和机器学习模型的基础，而模型通过数据进行训练，最终帮助做出优化决策。
• 数据提供了对问题的理解，模型则用来将数据转化为有意义的信息，决策则基于模型的输出进行实施，最终影响实际操作或结果。

5. 总结

这张图片强调了机器学习与优化技术的深度融合，并且展示了在未来优化问题中，数据将扮演越来越重要的角色。通过结合数据分析、机器学习和优化模型，能够在许多复杂的实际问题中找到更精确、高效的解决方案，推动各行各业的技术进步和创新。

这张图片讨论了数据分析中的三个关键领域：描述性分析（Descriptive）、预测性分析（Predictive） 和 规范性分析（Prescriptive）。这些分析方法是数据驱动决策的基础，并且通过不同的方式帮助我们理解数据、预测未来的趋势以及做出优化决策。

1. 描述性分析（Descriptive Analytics）

• 数据采集与管理：描述性分析主要关注数据的收集和管理，是数据分析的基础。通过收集并整理数据，描述性分析帮助我们理解过去发生了什么事情。
• 作用：它帮助我们回答“发生了什么”的问题，例如：
  • 数据收集与整理：组织数据，清洗和格式化数据，使其适合进一步的分析。
  • 数据总结：通过统计数据和可视化手段，提供一个整体的理解，帮助决策者掌握业务的现状。

2. 预测性分析（Predictive Analytics）

• 规律分析：预测性分析侧重于基于历史数据来识别趋势和模式，从而预测未来的情况。它主要通过统计学和机器学习技术，分析历史数据来预测可能发生的事件。
• 作用：预测性分析帮助我们回答“未来可能会发生什么”的问题。例如：
  • 基于历史数据的趋势分析：例如，利用过去的销售数据来预测未来的销售。
  • 风险预测：通过分析潜在风险的模式来预测未来可能发生的风险事件。

3. 规范性分析（Prescriptive Analytics）

• 优化与决策：规范性分析是数据分析中最为复杂的一部分，它不仅仅是预测未来，还提供了优化方案，帮助决策者选择最佳行动方案。它通过数学建模和优化算法，提出能够改进决策的方案。
• 作用：规范性分析帮助我们回答“我该怎么做”的问题，即给出最优的行动策略。例如：
  • 通过优化算法来决定最优的资源配置和生产调度方案。
  • 在面对复杂的业务决策时，提供推荐方案，以提高效率、降低成本并最大化利润。

4. 数据驱动决策的三大关键

• 数据采集与管理：收集和清洗数据，确保数据质量，为后续的分析奠定基础。
• 模型：使用预测性分析建立数学模型，揭示数据背后的规律，帮助预测未来趋势。
• 决策：通过规范性分析，应用优化模型来做出最佳决策，从而实现目标的优化。

5. 总结

数据分析不仅仅是查看数据，它涉及从历史数据中提取有用的信息、预测未来趋势以及制定优化的决策方案。随着数据科学的进步，描述性分析、预测性分析和规范性分析的结合，使得各行业能够更有效地利用数据做出更加精确的决策，提升效率、降低成本并创造更大的价值。

这张图片展示了运筹学的知识结构和前置知识要求。左侧的思维导图列出了运筹学的核心内容和相关知识点，右侧则展示了《运筹学教程》一书的封面。以下是详细的解读：

1. 运筹学的知识结构

1.1 运筹学的主要领域

运筹学是一个广泛的学科，涵盖了多种分析和优化方法。以下是运筹学中一些主要的领域和知识点：

• 目标规划：运筹学的核心问题是如何优化目标函数，找到最优解。这要求了解目标函数的构建和约束条件的处理。
• 数学规划：包括线性规划（LP）、整数规划（IP）、非线性规划（NLP）等方法。
• 排队论（Queuing theory）：用于分析和优化排队系统，广泛应用于服务业、计算机网络、制造业等领域。
• 库存理论（Inventory theory）：研究如何有效管理库存，平衡存货成本和需求。
• 博弈论（Game theory）：涉及多方决策问题，分析不同参与者在冲突或竞争中的最佳策略。
• 决策理论（Decision theory）：为决策者提供制定最优决策的方法，尤其是在不确定性条件下。
• 网络分析与设计（Network analysis and design）：运筹学在网络设计中的应用，优化如交通流、通信网络等系统。
• 动态规划（Dynamic programming）：解决具有多阶段决策过程的问题，特别是带有递归性质的问题。

1.2 前置知识

• 数学基础：线性代数、微积分、概率论和统计学等。
• 计算机科学：运筹学的许多方法需要通过计算机程序实现，了解算法和编程语言是必不可少的。
• 运筹学的起源与发展：了解运筹学的历史和基本理论，有助于更好地理解其应用。

2. 《运筹学教程》

• 右侧展示的是一本名为《运筹学教程》的书籍封面。书中可能详细介绍了运筹学的基础知识、各种优化方法及其应用，帮助读者系统学习运筹学的核心内容。

3. 总结

这张图片通过思维导图展示了运筹学的核心知识领域，并列出了学习运筹学的前置知识要求。这些内容为学习运筹学提供了结构化的框架，并指引读者从理论到实践逐步掌握运筹学的精髓。

这张图片展示了优化领域的知识组成与前置知识。它以树状图的形式详细展示了优化（Optimization）在不同类别中的细分，并且突出了各种类型优化问题的细节。以下是对该图的详细解读：

1. 优化（Optimization）

• 优化（Optimization） 是运筹学和数学建模中的核心概念，目标是找到在给定约束条件下使目标函数最优的决策。优化问题通常分为几类，根据其特征、约束类型等不同进行分类。

2. 按不确定性分类（Uncertainty）与确定性分类（Deterministic）

• 不确定性优化（Uncertainty）：这类问题考虑了外部环境的不确定性，常见的有：

  • 随机规划（Stochastic Programming）：通过考虑不确定性因素来制定决策方案。
  • 鲁棒优化（Robust Optimization）：确保解在各种可能的环境下依然具有较好的表现。

• 确定性优化（Deterministic）：假设所有信息已知且不发生变化，常见的类型包括：

  • 多目标优化（Multiobjective Optimization）：解决需要同时优化多个目标的问题。
  • 连续优化（Continuous）：在连续变量的情况下进行优化，通常用于设计、控制等问题。
  • 离散优化（Discrete）：变量是离散的，如整数规划等。

3. 按约束类型分类（Constrained vs. Unconstrained）

• 无约束优化（Unconstrained）：在此类问题中，优化变量没有任何限制。包括：

  • 非线性最小二乘（Nonlinear Least Squares）：解决最小化非线性误差平方和的问题。
  • 非线性方程（Nonlinear Equations）：求解非线性方程组。
  • 不可微优化（Nondifferentiable Optimization）：目标函数或约束函数不具备导数。
  • 全局优化（Global Optimization）：寻找全局最优解的优化方法。
  • 非线性编程（Nonlinear Programming）：目标函数或约束条件为非线性。

• 有约束优化（Constrained）：在这些问题中，优化变量受特定约束的限制。包括：

  • 半定规划（Semidefinite Programming）：处理半正定矩阵相关的优化问题。
  • 半无限规划（Semifinite Programming）：涉及有限约束的无限变量优化问题。
  • 数学规划与平衡约束（Mathematical Programs with Equilibrium Constraints）：适用于含有平衡条件的优化问题。

4. 其他类型的优化

• 整数规划（Integer Programming）：在问题中，决策变量是整数或二进制变量。
• 组合优化（Combinatorial Optimization）：涉及离散变量的组合问题，优化目标通常是排列、组合等问题。
• 网络优化（Network Optimization）：用于网络流、路由选择等问题，优化网络的传输效率。

5. 其他具体优化方法

• 混合整数非线性规划（Mixed Integer Nonlinear Programming）：结合了整数规划和非线性优化问题。
• 界限约束（Bound Constrained）：优化问题中存在变量的上下界。
• 线性约束（Linearly Constrained）：问题中有线性约束。

6. 优化问题中的补充问题（Complementarity Problems）

• 这些问题涉及互补约束和变量之间的非线性关系，广泛应用于经济学和市场模型中。

7. 总结

这张图片提供了优化领域广泛的分类，帮助我们理解不同类型的优化问题。每个优化问题的特点和要求决定了求解方法的选择。例如，随机问题需要使用随机规划或鲁棒优化，而确定性问题则可以使用传统的线性规划、整数规划或非线性编程等方法。这些知识的结合帮助解决各种实际问题，涉及到工程、金融、交通等多个领域。

这张图片展示了运筹学课程的知识组成与前置课程要求。它根据不同的学习阶段划分了基础课程、核心课程和高级课程，并列出了每个阶段所需的知识和技能。以下是详细解读：

1. 基础课程（Level 0）

• 微积分（Calculus）：学习数学分析的基础工具，掌握微分与积分的基本概念和应用。
• 线性代数（Linear Algebra）：学习矩阵、向量空间、特征值等基础内容，是运筹学的基础。
• 概率与数理统计（Probability and Statistics）：了解概率论和统计学的基本概念和方法，为分析不确定性和数据分析打下基础。
• 运筹学导论（Introduction to Operations Research）：学习运筹学的基本概念、方法和应用领域。
• 编程（Programming）：掌握至少一种编程语言（如Python、MATLAB等），用于解决运筹学中的计算和建模问题。

2. 核心课程（Level 1）

• 线性规划（Linear Programming）：学习优化问题中最基本的一类，涉及线性目标函数和线性约束条件。
• 非线性规划（Nonlinear Programming）：研究目标函数或约束条件是非线性的优化问题。
• 整数规划（Integer Programming）：解决部分决策变量是整数的优化问题，常用于调度、分配等实际问题。
• 大规模模型优化（Large-Scale Model Optimization）：学习如何求解大规模优化问题，涉及计算复杂度、内存优化等问题。
• 凸优化（Convex Optimization）：研究凸函数的优化问题，凸优化在许多工程和金融问题中都有应用。
• 多目标优化（Multi-Objective Optimization）：解决多个目标函数同时优化的问题，适用于很多实际决策问题，如资源分配。

3. 高级课程（Level 2）

• 随机优化（Stochastic Optimization）：处理存在不确定性的优化问题，适用于风险管理、金融优化等领域。
• 鲁棒优化（Robust Optimization）：优化模型考虑数据和环境的不确定性，确保方案的稳定性。
• 分布式鲁棒优化（Distributed Robust Optimization）：处理分布式系统中的鲁棒优化问题。
• 预测优化（Predictive Optimization）：结合预测模型来进行优化，广泛应用于供应链管理等领域。
• 动态优化（Dynamic Optimization）：处理时间相关的优化问题，例如多阶段决策问题。
• 马尔科夫决策过程（Markov Decision Processes）：用于决策问题中，状态转移遵循马尔科夫性质的问题。
• 近似算法（Approximation Algorithms）：解决一些难以精确求解的优化问题，利用近似方法获得可接受的解决方案。
• QCP（Quadratically Constrained Programming）与半线性规划（Semidefinite Programming）：涉及二次约束优化和半线性约束优化问题。

4. 总结

这张图清晰地列出了运筹学各个层次的知识内容，从基础的数学工具到高级的优化方法。每个阶段的课程逐渐深入，要求学生掌握越来越复杂的数学模型和优化方法。通过这样的课程安排，学生能够从基础理论到高级应用，全面掌握运筹学的各类知识和技能，为实际决策提供支持。

这张图片展示了高级课程的知识组成与前置要求。通过思维导图的方式，清晰地列出了学习高级课程所需掌握的基础知识和相关技能。

1. 基础课程要求

• 微积分（Calculus）：这是许多高级数学和优化问题的基础，学生需要理解微分和积分的基本概念。
• 线性代数（Linear Algebra）：学习矩阵、向量、线性变换等概念，是优化和建模中的基础工具。
• 概率论与数理统计（Probability and Statistics）：理解数据的不确定性、概率分布、统计推断等内容，在数据分析和优化中至关重要。
• 数学分析（Mathematical Analysis）：深入理解函数、极限、连续性等基本数学概念，有助于解决更复杂的数学问题。
• 数值计算（Numerical Computing）：使用计算方法解决数学模型中的数值问题，特别是在求解大规模问题时非常重要。

2. 高级课程内容

• 模型与数据分析：学生需要学习如何通过数据建模、回归分析和其他统计方法来分析问题。重点包括：
  • 回归分析：如何通过回归模型建立变量之间的关系。
  • 多元回归分析：在回归分析中加入多个变量，以更好地拟合实际问题。
• 模拟与优化方法：包括如何利用蒙特卡洛模拟（Monte Carlo）、优化算法等方法来求解复杂问题。
• Bootstrap方法：这是一种基于计算的统计学方法，用于估计统计量的分布。

3. 高级课程知识点

• 算法与编程：学生需要掌握编程语言（如Python、MATLAB等），并能应用于数据分析和模型求解中。
• 多目标优化（Multi-Objective Optimization）：解决多个目标需要同时优化的问题，广泛应用于资源分配、设计优化等领域。
• 非线性模型与求解：处理目标函数和约束条件为非线性的优化问题。
• 数据分析工具：包括如何使用Excel等工具进行数据分析和建模。

4. 应用场景

• 统计分析与建模：在实际应用中，学生需使用这些方法和技能进行数据的深入分析和建模。
• 决策支持系统：运用优化方法和统计工具，帮助做出最优决策，广泛应用于企业运营、物流调度等领域。

5. 总结

这张图总结了学习高级课程所需的前置知识和技能，从基础的数学工具到更复杂的模型和优化技术，每一层级的知识都为学生提供了必要的技能基础，使他们能够解决实际的优化问题。这些课程内容不仅在学术研究中至关重要，也能为学生进入工业界提供强有力的支持。

这张图片展示了与知识结构、前置要求以及就业方向相关的信息，尤其针对管理科学与工程专业的学生。以下是详细解读：

1. 考研方向：管理科学与工程专业

• 该专业的学生可以选择考研，进一步深入研究管理学、工程学和优化技术，通常与数据分析、决策支持系统和运筹学等相关。
• 管理科学与工程专业的考研方向，通常涉及到对复杂决策问题的数学建模、数据分析及优化算法的深入研究。

2. 竞赛

学生可以通过参加各种竞赛来提升自己的实践能力和创新思维：

• “互联网+”挑战杯：这是一个具有广泛影响力的比赛，参赛者通常需要解决实际问题，并提出创新的解决方案，涉及技术创新和商业应用。
• ACM竞赛：是全球著名的计算机科学竞赛，参赛者需要展示其编程能力和解决算法问题的能力。
• 全国大学生数学建模竞赛：此比赛强调数学建模、计算机应用和工程问题的解决，是应用数学与工程问题解决能力的展示平台。
• 服务外包比赛：通过解决实际的服务外包问题，参赛者展示其在优化、流程设计等领域的能力。
• 华为云大赛、阿里天池竞赛、京东大数据竞赛等：这些比赛侧重于数据分析、优化和机器学习等领域，参赛者通过实际项目来展示其解决复杂问题的能力。

3. 毕业设计与就业

• 毕业设计：学生在完成学业后，通常需要做一个综合性的毕业设计项目，结合所学知识，解决一个实际问题，展示其在数据分析、优化和决策支持方面的能力。
• 就业方向：毕业后，学生可以进入以下方向：
  • 数据分析（Data analytics）：数据分析是当前非常热门的职业方向，尤其是在大数据时代，企业和组织依赖数据来做决策。
  • 优化（Optimization）：优化技术广泛应用于制造业、物流、供应链管理、金融等领域，帮助企业提高效率、降低成本。
  • 数据可视化（Visualization）：数据可视化有助于将复杂的数据和模型结果转化为易于理解的图形和图表，支持更直观的决策过程。

4. 数据分析与优化结合

数据分析与优化技术的结合，将为学生提供更强的竞争力。数据分析帮助理解数据背后的趋势，而优化技术则帮助制定最佳决策，二者结合将在未来的工作中发挥关键作用。

5. 总结

这张图展示了管理科学与工程专业的学生如何通过参与竞赛和实践，提升自己的技能，最终将其应用于数据分析、优化决策和数据可视化等领域。专业知识、实际操作能力和创新思维将是学生未来成功的关键因素。

这张图片展示了优化问题的研究范围，通过不同的输入类型和问题特征将优化问题分为四个主要类别。以下是对这些类别的详细解读：

1. 静态与确定性问题（Static and Deterministic）

• 静态问题：静态优化问题指的是不涉及时间变化的优化问题，所有的决策和参数都是固定的，不随时间推移而变化。
• 确定性输入：确定性输入意味着问题中的所有数据都是已知的，未来没有不确定性，问题的所有变量和参数都是可以精确控制和预见的。
• 典型应用：这类问题通常涉及经典的线性规划、整数规划等问题，例如：生产调度、资源分配等问题。

2. 静态与随机输入（Static and Stochastic）

• 静态问题：与上述相同，问题本身没有时间的变化。
• 随机输入：随机输入意味着问题中包含随机变量或不确定性因素，未来的某些参数（如需求量、供应量、市场变化等）是未知的或有一定的概率分布。
• 典型应用：例如，在不确定市场条件下进行库存管理或定价决策，或者在金融领域的投资组合优化。

3. 动态与确定性问题（Dynamic and Deterministic）

• 动态问题：动态优化问题涉及随时间变化的决策问题。即决策不仅仅是在一个时间点上做出的，而是根据时间进程和状态变化来动态地调整决策。
• 确定性输入：这里的输入数据仍然是已知的，未来不含有随机性。
• 典型应用：如多阶段的决策问题，常见于供应链优化、库存控制等问题，决策者需要根据当前状态和未来的预测进行逐步决策。

4. 动态与随机输入（Dynamic and Stochastic）

• 动态问题：问题本身是动态的，涉及时间的推移和状态的变化。
• 随机输入：问题中的输入不仅随时间变化，还包括不确定性因素，未来的某些数据是随机的，可能具有一定的概率分布。
• 典型应用：这类问题是最为复杂的，广泛应用于金融工程、库存控制、能源调度等领域。决策者需要在不确定和动态环境中不断调整策略。

5. 总结

这张图通过将优化问题分为四类，清晰地展示了如何根据不同的输入类型和问题的时间特性来分类优化问题。在实际应用中，很多问题往往是这几类的组合。例如，现代供应链问题既有时间变化，又涉及不确定性因素，因此需要同时考虑动态性和随机性。在研究和解决这些问题时，选择合适的优化方法至关重要。

这张图片展示了**大规模混合整数规划（MIP）**问题的矩阵/向量表示和扩展形式。

1. 矩阵/向量表示（Matrix/Vector Representation）

这是混合整数规划（MIP）问题的一种简化表示方法，通常用于数学建模和算法求解。具体形式为：

• 目标函数：最小化 ( c^T x )，其中 ( x ) 是决策变量向量，( c ) 是目标函数的系数向量。
• 约束条件：( A x \geq b )，其中 ( A ) 是约束的系数矩阵，( x ) 是决策变量向量，( b ) 是约束的右侧向量。
• ( x \in \mathbb{Z}_+^n )：表示决策变量 ( x ) 是非负整数。

这种表示方式能够紧凑地描述线性约束和目标函数，并用于计算机算法中进行求解。

2. 扩展形式（Expanded Form）

扩展形式是将矩阵/向量表示转换为具体的线性方程形式，能够直观地展示各个约束条件。

• 目标函数：( \min \sum_{j=1}^{n} c_j x_j )
• 约束条件：每个约束条件的展开形式为线性方程，例如：
  [
  a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n \geq b_1
  ]
  这表示每个约束条件都可以展开为多个变量的加权和，具有明确的数学意义。

这种展开形式通常用于数学推导、模型验证和问题分析，使得每个约束条件的具体含义更加清晰。

3. 总结

这张图片展示了大规模混合整数规划问题的两种常见表示形式。矩阵/向量表示通常用于简洁表达和计算机求解，而扩展形式则能帮助我们更好地理解模型的具体细节。MIP广泛应用于各种优化问题，尤其是在需要决策变量为整数时，涉及的问题通常较为复杂，需要高效的求解方法（如分支限界法、割平面法等）。

这张图片展示了如何研究线性规划（LP）和整数规划（IP），尤其是在大规模MIP问题的研究中。

1. 如何研究LP和IP（How to study LP and IP for research）

这部分提到研究线性规划（LP）和整数规划（IP）时需要掌握的三项关键技能或方法。

2. 几何直觉（Geometric intuition）

• 几何直觉：研究优化问题时，几何直觉起着重要作用。通过几何方法，可以帮助我们更直观地理解问题的结构和性质。例如，通过绘制约束的可行区域，我们可以直观地理解线性规划的可行解集和最优解的位置。
• 作用：几何直觉能让我们对优化问题有更清晰的认识，并且在此基础上进行一些推测和猜想，有助于问题的进一步分析与求解。

3. 代数运算（Algebraic manipulation）

• 代数运算是用于描述和推导优化问题的主要方法。通过代数操作，我们可以精确描述线性和非线性约束条件，以及目标函数的形式。
• 作用：代数方法帮助我们规范化问题的结构，并为求解过程提供理论支撑。通过这些工具，我们能够得到许多求解算法的推导和证明。

4. 计算机编程（Computer programming）

• 计算机编程：运筹学和优化问题的求解通常涉及大量的计算和算法迭代。现代优化问题几乎都需要借助计算机来实现，尤其是大规模的问题。
• 作用：编程可以帮助我们实现迭代算法框架，从而求解复杂的LP和IP问题。计算机能够快速解决无法手工计算的大规模问题，因此编程是现代优化研究不可或缺的工具。

5. 总结

这张图片强调了研究LP和IP时，几何直觉、代数运算和计算机编程的三大核心技能。几何直觉帮助我们理解问题的本质，代数运算提供了数学化的工具，而编程则是实现这些工具和方法的关键。对于大规模MIP问题，计算机编程尤其重要，因为它能够处理复杂的计算和大量的数据。

这张图片展示了大规模混合整数规划（MIP）问题的研究范围，具体包括了线性规划（LP）、整数规划（IP）和大规模组合优化的相关内容。以下是详细分析：

1. 线性规划（Linear Programming）

• LP标准形式：这指的是线性规划问题的一般标准形式，通常包括目标函数的最大化或最小化，以及线性约束条件。
• LP如何求解：研究LP问题的求解方法，包括经典的单纯形法和内点法等。
• 单纯形法（Simplex Method）：这是求解线性规划问题最常用的算法之一，通过在可行解的顶点之间移动，找到最优解。
• 对偶理论（Duality Theory）：线性规划中的对偶理论帮助我们从问题的对偶形式中获得更多的优化信息。通过对偶问题的求解，通常可以获得原问题的最优解或者提供下界/上界。
• 内点法（Interior Point Methods）：内点法是一种解决线性规划问题的现代方法，通常用于大规模线性规划问题，具有较好的收敛性能。

2. 整数规划（Integer Programming）

• 基本认识：整数规划问题是一类特殊的线性规划问题，其中部分或全部决策变量必须取整数值。
• 分支限界法（Branch and Bound, B&B）：这是一种用于求解整数规划问题的常见方法。通过递归地分割问题空间，并对每个子问题进行求解，利用上下界剪枝来减少计算量。
• 割平面法（Cutting Plane）：割平面法是另一种用于求解整数规划问题的技术，主要通过将可行区域分割成更小的区域，从而得到整数解。

3. 大规模组合优化（Large Scale Combinatorial Optimization）

• 分支定界（B&B）：分支定界法是一种广泛使用的算法，适用于解决各种组合优化问题，例如整数规划问题。它通过分割问题空间来逐步逼近最优解。
• 分支定价（B&P）：分支定价法结合了分支定界法和列生成技术，主要应用于处理大型整数规划问题。
• 分支切割（B&C）：分支切割法是分支定界法和割平面法的结合，适用于整数规划和混合整数规划问题。
• 拉格朗日松弛（Lagrangian Relaxation）：通过松弛一些约束，使问题变得更容易解决，然后利用拉格朗日乘子调整松弛度。
• 列生成（Column Generation）：用于处理大型整数规划问题的技术，逐步生成新的列，以优化目标函数。
• DW分解与Benders分解（DW and Benders Decomposition）：这些方法常用于大规模优化问题的分解与求解，尤其在多阶段决策问题中，能够通过分解技巧来简化求解过程。

4. 总结

这张图片概述了大规模混合整数规划（MIP）问题的不同方面，涵盖了线性规划、整数规划的基础知识和相关算法，以及如何将这些算法应用于大规模组合优化问题。通过掌握这些方法，研究人员可以有效地解决复杂的优化问题，尤其是在工业和工程应用中。

这张图片展示了**大规模混合整数规划（MIP）**研究的不同学习和研究阶段。它将研究内容分为三个层次，分别是基础层次、核心层次和高级层次。以下是每个层次的详细解读：

1. Level 0: 基础层次（Modeling + Tools）

• 建模（Modeling）：在这一阶段，学习的重点是掌握如何建立优化模型，理解如何将实际问题转化为数学模型，这对于优化问题的求解至关重要。
• 工具（Tools）：此阶段需要掌握一些优化求解工具，例如：
  • Cplex：一个广泛使用的线性规划和整数规划求解器，能够高效求解各种优化问题。
  • Gurobi：另一个强大的优化工具，支持各种线性、非线性及整数优化问题。
  • 其他工具：还包括其他可能的建模和求解工具。

2. Level 1: 核心层次（Modeling + Heuristic Algorithms）

• 建模（Modeling）：继续加强优化问题建模的能力，尤其是在面对复杂的实际问题时，如何通过合适的建模技巧进行问题抽象和表达。
• 启发式算法（Heuristic Algorithms）：学习并应用一些启发式算法，以解决大规模和复杂的优化问题。常见的启发式算法包括：
  • 分支限界法（Branch-and-Bound, B&B）：一种常用的求解整数规划问题的算法，通过分治法来缩小问题的搜索空间。
  • 分支与切割法（Branch-and-Cut, B&C）：结合了分支限界法和割平面法，用于求解更加复杂的整数规划问题。

3. Level 2: 高级层次（Advanced Modeling Techniques, Decomposition Techniques, B&P&C）

• 高级建模技术（Advanced Modeling Techniques）：学习更加复杂的建模方法，能够处理更为复杂的约束、非线性问题或更大规模的问题。
• 分解技术（Decomposition Techniques）：学习如何将大规模的优化问题分解为多个更容易处理的小问题，这些技术有助于提高求解效率，常用于大规模优化问题。
• 分支与定价法（Branch-and-Price）：一种结合了分支限界法和列生成技术的方法，适用于求解具有大量变量的整数规划问题。
• 分支与切割法（Branch-and-Cut）：继续研究分支与切割技术的扩展和应用。

4. 总结

这张图提供了大规模混合整数规划（MIP）研究的路径。通过从基础的建模和工具使用，到核心的启发式算法，再到更高级的分解技术和优化方法，逐步建立起全面的优化求解能力。理解这些层次的内容，将帮助学生和研究人员逐渐掌握求解大规模优化问题的技能，并在实际应用中取得更好的效果。

这张图片展示了经典的整数规划（IP）问题，涵盖了多个领域中的常见优化问题。以下是对这些经典问题的详细解析：

1. 背包问题（Knapsack Problem）

背包问题是经典的整数规划问题之一，通常用于资源分配和最大化效益的场景。

• 0-1背包问题（0-1 Knapsack Problem）：每个物品只能选择放入背包或者不放，目标是最大化背包的总价值。
• 整数背包问题（Integer Knapsack Problem）：物品可以选择多次，目标是最大化总价值，且每个物品的选择次数是有限的。
• 多维背包问题（Multidimensional Knapsack Problem）：涉及多个约束维度，例如，物品在多个资源限制下的分配问题。

2. 指派问题（Assignment Problem）

指派问题通常用于任务分配和资源调度问题。

• 0-1指派问题（0-1 Assignment Problem）：每个任务只能被分配给一个资源，目标是最小化成本或最大化效益。
• 二次指派问题（Quadratic Assignment Problem）：在此问题中，目标函数是二次的，通常涉及设施布局等复杂问题。
• 广义指派问题（Generalized Assignment Problem）：允许更多复杂的任务与资源之间的关系，如任务需要多个资源的情况下。
• 匹配问题（Matching Problem）：涉及两个集合的元素之间的匹配，例如，在二分图中找到最大匹配。

3. 与集合相关的问题（Set Covering Problems）

集合覆盖问题通常涉及如何选择最少的集合来覆盖所有元素。

• 集合覆盖问题（Set Covering Problem）：选择最少的子集以覆盖所有元素。
• 划分问题（Partition Problem）：将集合划分为若干子集，目标是最小化划分的差异。
• 包裹问题（Packing Problem）：选择不同的元素进行优化，通常是为了最大化资源的使用。

4. 与网络相关的问题（Network Problems）

网络优化问题在物流、运输、通信等领域非常常见。

• 最小费用网络流问题（Minimum Cost Flow Problem）：在网络中寻找最小费用的流量配置。
• 最大流问题（Maximum Flow Problem）：计算在给定网络中能流动的最大流量。
• 最短路径问题（Shortest Path Problem）：计算从一个节点到其他节点的最短路径。
• 多商品流问题（Multicommodity Flow Problem）：涉及多种商品在网络中的流动，优化各条路径上的流量。

5. 与选址相关的问题（Location Problems）

选址问题广泛应用于物流、供应链管理、设施布局等领域。

• 设施选址问题（Facility Location Problem）：优化设施（如仓库、工厂等）的位置选择，以最小化总成本或最大化服务效益。

6. 与路径相关的问题（Routing Problems）

路径规划问题广泛应用于交通运输、物流调度等领域。

• 旅行商问题（TSP, Traveling Salesman Problem）：找到一条最短的路径，使得销售员能够访问所有城市，并且每个城市只访问一次。
• 车辆路径问题（VRP, Vehicle Routing Problem）：优化车辆的路径，以最小化总运输成本，广泛应用于快递、运输调度等领域。

7. 与机器生产相关的问题（Machine Production Problems）

这些问题通常涉及生产调度和工作流的优化。

• 流水车间问题（Flow Shop Problem）：优化生产过程中多个工序的排列，以最小化生产总时间。
• 作业车间问题（Job Shop Problem）：在多个机器之间安排作业，以最小化总的生产时间。

8. 总结

这张图列举了许多经典的整数规划问题，涵盖了从资源分配、任务调度到网络流和路径优化等多个领域。每类问题都有其独特的求解方法和应用场景，通过这些问题的研究和优化，能够帮助解决实际中的复杂决策问题。这些经典问题也是运筹学和优化学科的基础，广泛应用于实际的工业、交通、物流等领域。

这张图片展示了不确定性优化（Optimization under Uncertainty）的研究范围，并引用了两位著名人物的名言：

1. 研究范围：不确定性下的优化（Optimization under Uncertainty）

• 该部分强调了在不确定性条件下进行优化的问题。这是优化学中的一个重要领域，涉及如何在面对不确定因素时做出最优决策。由于很多实际问题中存在大量的不确定性（如市场需求、生产时间、供应链延误等），因此不确定性优化在许多领域中具有广泛应用，如金融、供应链管理、工程设计等。

2. 引用的名言

• 伏尔泰（Voltaire）：“不确定性是一个不舒服的状态，但确定性是一个荒谬的状态。” 这句话传达了不确定性在实际生活中无处不在，而过于依赖确定性可能会导致不切实际的预期。优化问题中往往会遇到不确定性，解决这些问题需要考虑如何在不完全信息下做出最佳决策。

• 乔治·丹齐格（George Dantzig）：他是线性规划的奠基人之一，他在其85岁生日时提到：“我致力于不确定性下的规划。这是我认为最重要的领域，也是未来的发展方向。” 这句话表明了不确定性优化问题在运筹学和优化领域中的重要性，并且展望了这一领域的未来发展。

3. 总结

这张图片强调了不确定性优化的重要性。随着技术的发展和现实世界问题的复杂性增大，如何在不确定的条件下做出决策和优化，已经成为学术界和工业界关注的核心问题之一。在许多实际应用中，优化决策不仅仅依赖于确定的参数，还需要考虑多种可能的变化因素。因此，研究不确定性优化问题具有重要的理论和实践意义。

这张图片展示了不确定性优化的应用案例，尤其是与路径选择和旅行时间相关的优化问题。

1. 背景描述

在这个例子中，研究的目标是如何在存在不确定性的情况下选择最佳路线。我们有两条从地点 A 到地点 B 的路线，且每条路线的旅行时间存在不确定性。每条路线的预计旅行时间和可能的变动范围都已知，目标是选择最佳路线，考虑不同情况下的期望时间和风险。

2. 路线选择与不确定性

• 路线 1：
  • 预计时间：12.4分钟，并且有80%的概率在20分钟内到达，有20%的概率超过20分钟。
• 路线 2：
  • 预计时间：12.2分钟，并且有95%的概率在20分钟内到达，有5%的概率超过20分钟。
• **不确定性分析：**在此场景中，不同的概率给出了每条路线可能的延迟时间，因此，在做出决策时，需要考虑的不仅是期望时间，还要考虑风险（如某条路线有较高的延迟概率）。

3. 第二个图示（不同概率和延迟）

• 路线 1：
  • 预计时间：10分钟，有80%的概率在10分钟内到达，20%的概率需要22分钟。
• 路线 2：
  • 预计时间：10分钟，但95%的概率只需10分钟，5%的概率需要54分钟。
• **不确定性分析：**在这种情况下，尽管两条路线的平均时间相同，但第二条路线的高风险（5%的概率需要54分钟）可能使其成为不理想的选择，特别是在高度重视时间的情境下。

4. 决策分析

• 风险与回报：不确定性优化的关键是权衡每个选择的平均效果和潜在的风险。在这个例子中，虽然路线 2的平均时间较低，但其高风险可能会导致不稳定的结果，尤其是在重要时间窗口内。
• **优化目标：**根据具体的需求（如是否容忍延迟），可以通过分析每条路线的概率分布和平均时间来做出最佳选择。

5. 总结

这张图展示了不确定性优化在路径选择中的应用，如何通过概率和平均值来评估不同选择的风险和回报。面对不确定性时，优化决策不仅要考虑期望结果，还需要评估潜在的风险（如延误的概率），这是实际应用中的一个重要考量。

这张图片展示了不确定性优化的不同方法和技术，特别是数据驱动的静态优化（Data-driven static optimization），以及几种解决不确定性问题的策略。以下是详细的解读：

1. 随机优化（Stochastic Optimization）

• 随机优化用于处理那些含有不确定性元素的问题。这些不确定性可能来自外部环境、需求波动、供应链变化等。目标是找到在不同随机环境下最优的解决方案。

2. 鲁棒优化（Robust Optimization）

• 鲁棒优化是一种优化方法，旨在考虑所有可能的不确定性，求解最坏情况下的最优解。通过鲁棒优化，可以在面对不确定性时确保解决方案在各种不利情况下都能达到良好的表现。

3. 随机模型（Stochastic Modeling）

• 随机模型考虑不确定性因素，使用概率分布来表示问题中的随机变量。该方法用于捕捉现实中不可预测的情况，并基于这些模型进行优化决策。

4. 马尔可夫决策过程（Markov Decision Process, MDP）

• 马尔可夫决策过程是用于决策分析的一种数学模型，特别适用于动态环境下的优化问题，其中未来的决策仅依赖于当前的状态，而不依赖于过去的状态。

5. 数据驱动的静态优化（Data-Driven Static Optimization）

• SAA（Sample Average Approximation）：样本平均近似方法，使用历史数据或样本数据来近似真实的随机分布，从而进行优化求解。
• Robust Optimization（鲁棒优化）：如上所述，鲁棒优化在数据驱动的框架下进一步加强了对不确定性的考虑，适用于决策中存在不确定性的情况。
• SP+O（Smart Prediction Then Optimize）：智能预测后优化方法，首先使用机器学习或其他方法预测未来的需求或情况，然后再进行优化决策。
• Retro（Retrospective Optimization）：回顾性优化方法，通过回顾过去的决策过程来优化未来的决策，常用于分析历史数据并找出改进的空间。
• Advo（Adversarial Optimization）：对抗性优化，通常涉及对抗模型，在优化过程中考虑到不确定性和恶意行为的可能性。
• ODA（Operational Data Analytics）：运作数据分析，通过实时收集和分析操作数据，帮助进行更灵活和快速的决策。

6. 总结

这张图片展示了不确定性优化的多种方法，强调如何通过数据驱动的策略来优化决策。面对不确定的环境，优化问题不仅依赖于传统的优化方法，还需结合数据分析和预测技术，帮助制定更加稳健的决策方案。

这张图片展示了不确定性优化的几种常见方法，包括随机规划（Stochastic Programming）、鲁棒优化（Robust Optimization）和分布式鲁棒优化（Distributionally Robust Optimization）。以下是每种方法的详细解读：

1. 随机规划（Stochastic Programming）

• 已知的概率分布：随机规划通常假设问题中的不确定性可以通过已知的概率分布来描述。目标是在这种不确定性下寻找最优解。
• 期望值最小化：在这种方法中，优化目标是最小化期望值，表达式为：
  [
  \min_x \mathbb{E}_p[f(x, \tilde{d})]
  ]
  其中，( f(x, \tilde{d}) ) 是目标函数，( p ) 是不确定性参数 ( \tilde{d} ) 的概率分布，( \mathbb{E}_p ) 表示对不确定性因素进行期望计算。
• 应用场景：适用于那些概率分布已知且可以使用统计数据进行建模的优化问题。

2. 鲁棒优化（Robust Optimization）

• 不确定性集：鲁棒优化关注的是在不确定性条件下对最坏情况的优化。其核心是定义一个不确定性集，这个集包含了所有可能的输入值，常见的不确定性集有：
  • 有界支撑集（Bounded support）
  • 多面体不确定性集（Polyhedral）
  • 预算不确定性集（Budgeted）
• 最坏情况性能：鲁棒优化的目标是最小化最坏情况下的目标函数。即：
  [
  \min_x \max_d f(x, \tilde{d})
  ]
  这里的 ( \tilde{d} ) 是不确定性变量，优化是在最坏情况下进行的。
• 应用场景：鲁棒优化特别适用于那些面临严重不确定性，并且需要保证在最坏情况下也能获得好的解的情况。

3. 分布式鲁棒优化（Distributionally Robust Optimization）

• 模糊不确定性集（Ambiguity set）：分布式鲁棒优化考虑的是不确定性分布本身的不确定性，即我们对概率分布的知识不完全，存在模糊性或不确定性。它通常定义一个不确定性分布的集合，称为模糊不确定性集。
• 最坏情况分布：其优化目标是通过考虑所有可能的分布，最小化在最坏情况下的目标函数：
  [
  \min_x \sup_{p \in \mathcal{F}} \mathbb{E}_p[f(x, \tilde{d})]
  ]
  这里的 ( \mathcal{F} ) 是可能的概率分布集，目标是最大限度地降低最坏情况的风险。
• 应用场景：适用于当我们无法完全知道不确定性分布，但仍需要对不确定性进行建模并优化决策的情况。

4. 总结

这张图展示了处理不确定性问题的三种主要方法，它们的核心区别在于如何定义和处理不确定性：

• 随机规划假设不确定性有已知的概率分布。
• 鲁棒优化关注最坏情况下的表现，适用于不确定性范围已知的情况。
• 分布式鲁棒优化考虑不确定性分布的不确定性，适用于不完全知道概率分布的情况。

这些方法为解决具有不确定性的优化问题提供了不同的视角和技术，广泛应用于供应链管理、金融决策、工程设计等领域。

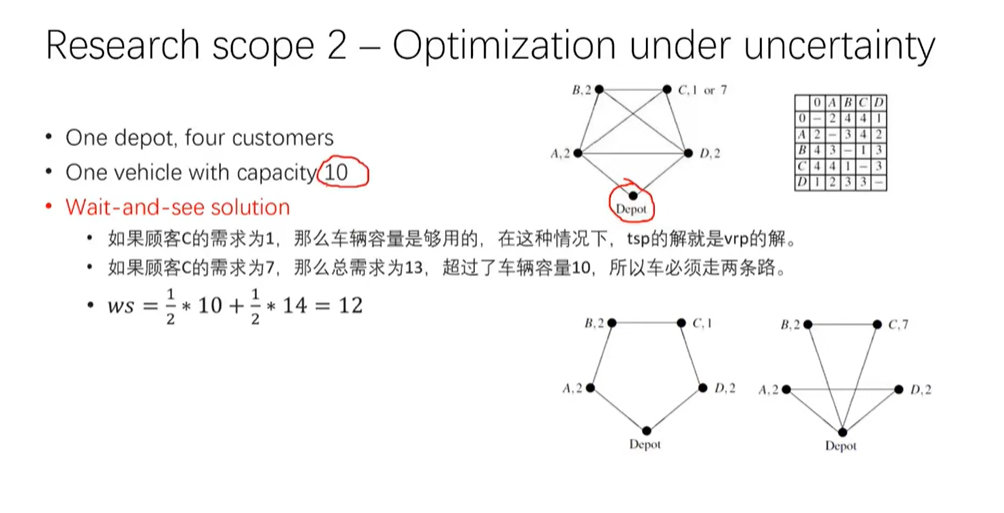
这张图片展示了不确定性下的优化应用，具体是与车辆路径规划（Vehicle Routing Problem, VRP）相关的例子。以下是对该场景的详细分析：

1. 问题描述

• 仓库（Depot）：这是车辆出发和返回的起点，通常是一个固定的地点。
• 四个客户（Four customers）：有四个不同的客户，每个客户的需求量是随机的（可能是不确定的）。
• 一辆容量为 10 的车辆：车辆的容量限制为10，这意味着每次只能运输最多10单位的货物。
• 路径规划：需要确定从仓库到客户的最佳路径，以便在满足容量限制的前提下完成所有客户的配送。

2. Wait-and-See Solution（等待与观察策略）

该策略涉及在知道所有需求量后再做决策。在这个例子中，我们首先计算两个可能的情景，并根据不同的客户需求量来选择适当的路径。

• 第一种情况：客户C的需求为1：

  • 如果客户C的需求量为1，那么车辆的容量足够，可以正常为客户C提供服务。在这种情况下，TSP（旅行商问题，Travelling Salesman Problem）的解就是VRP（车辆路径规划问题）的解。

• 第二种情况：客户C的需求为7：

  • 如果客户C的需求量为7，那么总需求量为13，超出了车辆的最大容量10。此时，车辆必须走两条路径才能完成配送。

3. 计算期望运输成本（Wait-and-See Expected Solution）

在等待与观察策略下，我们需要计算基于不同客户需求量的期望值。

• 期望值计算公式：
  [
  ws = \frac{1}{2} \times 10 + \frac{1}{2} \times 14 = 12
  ]
  其中，10是第一种情况（客户C需求为1）的路径成本，14是第二种情况（客户C需求为7）的路径成本。由于每种情况出现的概率是50%，所以我们取期望值。

4. 总结

该示例展示了在面对不确定性（如客户需求量不确定）的情况下，如何使用等待与观察策略来进行决策。通过根据不同情境的概率计算期望值，优化决策者可以做出更合适的路径规划决策。

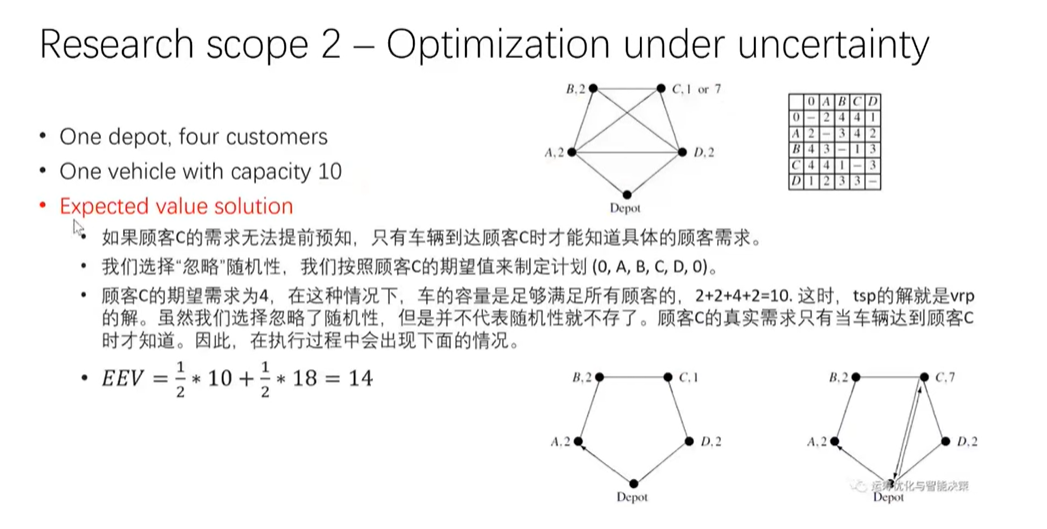
这张图片展示了不确定性优化在车辆路径规划问题（VRP）中的应用，具体内容涉及递归解法（Recourse solution）以及期望成本的计算。

1. 问题描述

• 一个仓库、四个客户：在此优化问题中，有一个仓库和四个客户需要配送，目标是为车辆路径选择最优方案。
• 一辆容量为 10 的车辆：车辆的最大容量为10，表示每次只能运输最多10单位的货物。

2. 递归解法（Recourse Solution）

该方法基于逐步决策的思想，其中在知道当前需求后做出最佳决策，然后继续执行后续的路径规划。

• 情况 1：客户C的需求为1：

  • 当到达客户C时，发现客户C的需求量为1，车辆能够满足该需求，并继续按照原计划执行。此时的路径规划是正常的，最终行驶距离为10。

• 情况 2：客户C的需求为7：

  • 如果在到达客户C时，需求量为7，超出了车辆的最大容量10。此时，车辆将需要进行一次额外的操作：先返回仓库再去配送其他客户。这样整个路径将变得更加复杂，最终的行驶距离为17。

3. 期望成本计算（Recourse Path Cost）

• 根据递归解法，期望的路径成本是根据不同的情境（客户需求为1或7）计算出来的。这里有50%的概率客户C的需求为1，50%的概率需求为7。
• 期望成本计算公式：
  [
  RP = \frac{1}{2} \times 10 + \frac{1}{2} \times 17 = 13.5
  ]
  这表示在这两种情境下，期望的行驶距离是13.5。

4. 一般规则（General Rule）

• 期望成本（WS）应小于或等于递归路径成本（RP），而递归路径成本应小于或等于期望效用值（EEV）。这个规则帮助我们评估不同策略下的优化效果。

  [
  WS \leq RP \leq EEV
  ]

• 这个规则表明，优化决策应该在递归求解的基础上，考虑到不确定性因素的影响，从而做出最优的决策。

5. 总结

• 这张图展示了在不确定性条件下，如何通过递归方法来优化车辆路径问题。通过计算不同需求情境下的路径成本，并结合期望值，可以帮助决策者做出更好的优化决策。在实际应用中，这种方法适用于物流、配送等具有不确定需求的场景。
  
  这张图片展示了不确定性下的优化中的一个应用方法：先预测再优化（Predict then Optimize）。具体来说，方法结合了智能预测与优化（Smart Predict + Optimization）以提高决策质量。

1. 预测后优化（Predict then Optimize）

• 在面对不确定性时，我们通常首先通过预测来了解未来可能的情况，然后基于这些预测结果进行优化决策。此方法结合了机器学习和传统优化技术。
• 这个方法主要分为两部分：
  • 智能预测（Smart Prediction）：利用模型（如回归、分类、深度学习等）对未来的不确定因素进行预测。
  • 优化（Optimization）：在获得预测结果后，运用优化方法选择最佳的决策。

2. 图1：回归模型与优化

• 回归模型：左侧的图展示了一个简单的线性回归模型，其中 ( y = mx + b ) 表示预测模型，目标是拟合一个直线（红色直线）来预测输入 ( x ) 对应的输出 ( y )。
• 优化公式：优化目标是最小化预测误差，公式如下：
  [
  \min \sum_{i} e_i^2, \quad y_i = m \cdot x_i + b + \epsilon_i, \quad x_i \in X
  ]
  其中 ( e_i ) 是误差项，( \epsilon_i ) 是预测误差。
• 该回归模型从数据点（灰色点）中学习，并通过调整线性函数的参数（斜率 ( m ) 和截距 ( b )）来最小化误差。

3. 图2：分类与黑箱模型

• 分类问题：右侧的图展示了一个分类问题，数据点被划分为不同的类别（如蓝色、绿色、红色等），这些类别可以对应不同的预测值（如 ( y_1, y_2, y_3 )）。
• 黑箱模型：图中的“黑箱”表示一个复杂的学习模型，如深度学习模型，通常用于处理无法直接解释的复杂数据。在这种模型下，输入 ( x ) 通过一个复杂的函数映射（( \phi )）到高维空间，再通过分类器进行预测。
• 相似性约束：模型通过学习找到相似的数据点，并确保它们具有相似的预测结果。即优化目标是使得所有输入 ( x \in X ) 和其预测 ( f(\phi(x)) ) 在相似性上匹配。

4. 总结

• 这张图展示了如何将智能预测和优化决策相结合，以应对不确定性。通过预测未来的不确定性因素并基于预测结果进行优化，可以在实际应用中做出更有效的决策。这种方法广泛应用于很多领域，如供应链管理、金融投资、工程设计等，尤其是在面临动态变化和复杂决策环境时。

这张图片展示了不确定性下的优化方法，特别是结合智能预测与优化的策略。这种方法的核心思想是首先通过预测模型对不确定性进行估计，然后基于预测结果做出最优决策。

1. 整体流程

• 数据（Data）：首先收集并使用相关的数据，这里示例为配送数据（Delivery Data），例如过去的运输记录、需求数据等。
• 预测模型（Prediction Model）：使用预测模型来估计未来的不确定性。例如，图中的不确定性信息（Uncertainty Information）描述了配送时间、需求等可能的变动情况。
• 解决方案（Solution）：根据预测模型和不确定性信息，利用优化方法找到最佳决策，从而最小化成本或提高效率。

2. 决策与分析类型

这张图通过三个不同的分析方式将问题联系起来：

• 描述性/预测性分析（Descriptive/Predictive Analytics）：这一部分侧重于从历史数据中提取信息并预测未来。这包括对配送数据的分析，确定需求量和可能的配送时间。
• 规范性分析（Prescriptive Analytics）：这一部分使用优化技术来推荐最优决策，比如确定运输路线、调度资源等。
• 估计/预测（Estimation/Prediction）：在这个阶段，我们使用预测模型（如回归分析、SVR等）来估算不确定性参数。

3. 模型与方法

下方列出了几种常见的预测模型，并评估了它们的可追踪性（Traceability）和可解释性（Interpretability）：

• LASSO, Ridge, Elastic Net：这些是线性回归的变种，适用于高维数据的回归分析。它们具有较好的可解释性，但在某些复杂数据上，可能没有深度学习方法那么强的预测能力。
• 线性支持向量回归（Linear SVR）：适用于回归任务，尤其是在数据存在噪声时表现良好，具有较好的可追踪性。
• RBF支持向量回归（RBF SVR）：使用径向基函数内核的支持向量回归，适用于复杂的非线性问题，具有较强的预测能力，但可解释性较差。
• 随机森林（Random Forest）：基于树的集成方法，适用于高维和非线性数据，具有较强的预测能力，但其决策过程的可解释性较低。

4. 总结

• 预测再优化结合了数据分析、预测建模和优化决策的三个步骤。通过智能预测模型，先估计不确定性因素，然后基于这些预测结果通过优化模型找到最优解。这种方法广泛应用于供应链、物流调度、金融风险管理等领域。
• 在选择合适的预测模型时，需要综合考虑模型的可追踪性和可解释性，尤其是在决策过程中能够理解模型的工作原理是非常重要的。

这张图片展示了动态过程中的确定性动态问题（Deterministic Dynamic Programming）。它重点讨论了如何在多个阶段中做出优化决策，并使用**动态规划（DP）**来解决问题。

1. 最优性原理（Optimality Principle）

• 最优性原理说明：如果一个决策序列是最优的，那么每个子序列也应该是最优的。这意味着，做出一个最优决策后，我们需要对每个子问题做出最优决策，确保每个阶段的决策都能引导到整体最优解。
• 这种方法尤其适用于多阶段决策问题（Multi-stage Decision Making Problems），其中每个阶段的决策都会影响到未来阶段的状态和最终结果。

2. 多阶段决策（Multi-stage Decision Making）

• 这类问题通常涉及多个阶段，每个阶段的决策不仅依赖当前状态，还会影响到后续的决策。每个阶段的优化目标都是找到在当前阶段下的最优决策，最终使整个过程达到最优。

3. 动态规划中的要素

• Stage ( k )：当前的阶段，通常表示决策过程中的一个时间步骤或阶段。
• State ( s_k )：当前阶段的状态，通常是问题的某个关键变量的值，决定了在当前阶段的决策。
• Action ( a_k )：在当前阶段的决策，即需要选择的行为或动作。
• Reward ( r_k )：在当前阶段做出决策后获得的回报或成本，通常是优化目标的一部分。

4. 动态规划应用

• 最短路径问题（Shortest Path Problem）：这是动态规划的一种经典应用，通过在每个阶段选择最短的路径，最终找到从起点到终点的最短路径。
• 顺序决策问题（Sequential Decision Problem）：在多个阶段的决策过程中，每个阶段的决策都会影响后续阶段的决策，动态规划可以帮助确定在各阶段的最优决策。
• 混合整数规划（MIP）：在涉及整数决策变量的优化问题中，动态规划也能应用于处理这些复杂的决策问题。

5. 示意图

图中显示了一个简单的网络图，展示了多阶段决策问题的结构。节点表示不同的状态，箭头表示从一个状态到另一个状态的转移，决策者在每个阶段根据当前状态做出决策（如选择路径）。

6. 总结

• 动态规划（DP）是解决多阶段决策问题的有效工具，尤其是在面对复杂的决策问题时，它通过分解问题，将大问题转化为多个小问题来求解最优解。通过最优性原理，动态规划能够有效地处理阶段性决策，并确保每个子问题的解能达到全局最优。

这张图片展示了随机动态（Stochastic Dynamic）中的一些核心概念，特别是与马尔可夫决策过程（Markov Decision Process, MDP）和强化学习（Reinforcement Learning, RL）相关的内容。

1. 随机动态（Stochastic Dynamic）

随机动态系统是指在一个不断变化的环境中进行决策的过程，其中未来的状态和奖励是随机的或不确定的。决策者（或智能体）需要根据当前状态做出决策，以最大化未来的奖励。

2. 马尔可夫决策过程（Markov Decision Process, MDP）

MDP 是一种数学模型，用于描述在不确定环境下的决策过程，包含以下要素：

• 状态（State ( S_t )）：在时间 ( t ) 时，系统的当前状态。
• 动作（Action ( A_t )）：在时间 ( t ) 时，智能体可以采取的行动。
• 奖励（Reward ( R_t )）：在采取某个动作后，系统给予的反馈奖励，通常是一个数值，用来衡量智能体的行为。
• 转移概率：描述从一个状态到下一个状态的概率分布。

最优性原则：根据马尔可夫决策过程，给定一系列最优决策序列，每个子序列也必须是最优的。

3. 强化学习（Reinforcement Learning, RL）

强化学习是机器学习中的一种方法，基于奖励和惩罚机制让智能体学会在环境中采取一系列行动，以最大化长期回报。智能体通过与环境的交互来学习最优策略：

• 智能体（Agent）：执行决策的主体，它根据当前的状态选择行动。
• 环境（Environment）：智能体与之互动的外部系统，它对智能体的行动做出反应，返回新的状态和奖励。
• 决策过程：智能体通过选择动作 ( A_t )，执行动作后，环境给出新的状态 ( S_{t+1} ) 和奖励 ( R_{t+1} )。
• 反馈机制：智能体的目标是最大化从环境中获得的奖励，因此它需要根据过去的经验（即从奖励中学到的策略）做出决策。

4. 图示说明

图示描述了强化学习中的智能体与环境的交互过程：

• **智能体（Agent）**从当前状态 ( S_t ) 开始，选择一个动作 ( A_t )。
• 环境根据选择的动作改变状态 ( S_t ) 并返回奖励 ( R_t )。
• 然后，智能体基于新的状态做出下一个决策，继续与环境互动。

5. 策略与目标

• 决策（Decision）：智能体在每个时间步根据当前状态选择最优的动作。
• 动作（Action）：智能体采取的行为，这会影响未来的状态和奖励。
• 奖励（Reward）：根据智能体的行动给出的反馈，用于指导智能体学习。
• 最大回报（Max Return）：智能体的目标是最大化它所获得的总回报，通常通过不断学习和优化决策策略来实现。

6. 总结

• 强化学习和马尔可夫决策过程是解决随机动态决策问题的两种重要方法。通过MDP模型，智能体能够在面对不确定性和随机性的环境下，通过与环境的交互来学习最佳的决策策略。
• 这种方法广泛应用于机器人控制、游戏AI、金融决策、自动驾驶等领域，特别是在环境变化和决策不确定性较高的情境下。

这张图片列出了与运筹学、管理科学、工业数学等领域相关的一些主要学术和研究组织，具体包括：

1. INFORMS 和 POMS

• INFORMS：Institute for Operations Research and the Management Sciences（运筹学与管理科学学会）。这是一个全球领先的运筹学和管理科学研究组织，致力于推动决策科学和优化方法的发展与应用。
• POMS：Production and Operations Management Society（生产与运营管理学会）。这个组织关注生产、运营管理以及相关的优化和管理科学问题，特别是在制造、物流、供应链等领域的应用。

2. 中国运筹学会

• 中国运筹学会（Chinese Operations Research Society，CORS）是运筹学和管理科学领域的一个重要学术组织，致力于推动国内外学者之间的合作与交流，并在中国推广运筹学的应用研究。

3. SIAM

• SIAM：Society for Industrial and Applied Mathematics（工业与应用数学学会）。这是一个国际学术组织，聚焦于数学在工业、工程和技术中的应用，促进数学与各学科领域之间的交流合作。

4. IET 和 IEEE

• IET：The Institution of Engineering and Technology（工程与技术学会）。这是一个致力于促进全球工程技术领域交流和发展的组织，成员遍布多个工程领域。
• IEEE：Institute of Electrical and Electronics Engineers（电气和电子工程师学会）。全球最大的技术专业组织之一，主要专注于电气工程、电子工程、计算机科学等领域，推动科学技术的创新与应用。

总结

这些学术组织为从事运筹学、优化、工业数学、工程学等领域的研究人员提供了一个良好的平台，促进了学术交流、研究合作与技术推广。

这张图片展示了全球运筹学与管理科学领域的主要研究组织的历史发展和时间线。从图中的信息可以看到这些组织在全球不同地区的建立和发展。

主要信息概览：

1. 国际运筹学与管理科学联合会（IFORS）

   • 成立时间：1955年。
   • IFORS 是全球运筹学与管理科学领域的主要国际组织，致力于促进学术研究、专业发展与国际合作。

2. INFORMS（运筹学与管理科学研究协会）

   • 成立时间：1998年。
   • INFORMS 是全球最大的运筹学学术组织之一，致力于推动运筹学在各行业的应用。

3. 其他重要的区域性组织

   • 欧洲运筹学会（EURO）：1972年成立，旨在促进欧洲地区的运筹学研究。
   • 亚洲运筹学会（APORS）：1985年成立，涵盖亚洲地区的运筹学活动。
   • 中国运筹学会（CORS）：成立时间：1958年，致力于推动运筹学在中国的发展。
   • 国际铁路运筹学会（IAROR）：专注于铁路运输领域的运筹学应用。
   • 运筹学与管理科学研究协会（MOS）：强调数学优化与运筹学的结合。
   • 运筹学与管理科学学会（CSIAM）：中国工业数学学会，专注于数学与工业领域的结合。

4. 运筹学与管理科学相关的辅助组织

   • AGIFORS：航空领域的运筹学组织，成立于1963年。
   • ORSSA：南非运筹学会，成立于1961年，专注于南非的运筹学发展。

5. 中国相关学会与协会

   • 中国运筹学会（CMS）：成立于1935年，是中国运筹学领域的奠基性学会。
   • 中国工业数学学会（CSIAM）：致力于工业数学的研究和应用。

总结：

这张图清晰地展示了运筹学与管理科学领域的一些国际和区域性学术组织的演变过程，并突出了它们在全球范围内的重要性和影响力。运筹学领域的研究组织不仅在促进学术交流和技术合作方面起着至关重要的作用，还推动了学术成果在各行各业的广泛应用。

这张图片显示了运筹学与管理科学（OR & MS）领域的重要期刊以及它们在UTD24 Journal List中的排名。

期刊列表

• Management Science（管理科学）
• Operations Research（运筹学）
• Journal of Operations Management（运营管理期刊）
• Manufacturing and Service Operations Management（制造与服务运营管理）
• Production and Operations Management（生产与运营管理）

这些期刊都在1990年加入了UTD24 Journal List，该列表是学术界广泛认可的期刊排名，特别适用于运筹学与管理科学（OR & MS）领域。

图片右侧的内容：

图片右侧展示了一个学术会议的场景，其中一位教授正在讲解运筹学的基本概念。演讲内容包括：

• 定义新的问题领域：为学科开辟新的研究方向。
• 创新概念的引入：为问题提出新的思路或新的数学公式。
• 为操作性问题提供新的见解：通过新的视角解决问题。
• 开发新方法论：为已知或新的问题开发新的方法论。
• 将运筹学方法应用于有趣的应用领域：促进运筹学方法与实际应用领域的结合。

总结：

这张图显示了运筹学与管理科学领域的顶级期刊，并强调了运筹学研究中的创新和方法论的重要性。

这张图展示了运筹学与优化的基本概念，以及建模与求解的框架，进一步阐述了运筹学中的不同类型问题与方法。

图中内容解析：

1. 优化模型的构建与求解：

   • 实际问题：从现实世界的问题出发。
   • 优化模型：将实际问题转化为数学模型，通常涉及决策变量、目标函数和约束条件。
   • 求解：应用优化算法求解模型，得到最优解。

2. 运筹学教材内容：

   • 图下部展示了典型的运筹学教材中的章节主题。包括：
     • 排队论（Queuing theory）
     • 库存理论（Inventory theory）
     • 博弈论（Game theory）
     • 决策理论（Decision theory）
     • 运筹学的创新发展方法。

3. 运筹学问题的分类：

   • 静态与确定性问题：所有参数已知且不随时间变化的优化问题。
   • 静态与随机问题：参数是已知的，但带有不确定性的优化问题。
   • 动态与确定性问题：问题在不同时间节点的决策中不断变化，且不涉及随机性。
   • 动态与随机问题：在时间和随机因素的双重影响下进行决策的问题。

4. 运筹学、机器学习与优化的关系：

   • 在右侧部分，图表展示了数据、模型和决策之间的关系，运筹学和机器学习（ML）如何结合来优化决策过程。数据流入模型，模型输出决策，并且模型基于数据做出预测。

总结：

这张图清楚地总结了运筹学在实际问题中的应用流程，涉及了从问题建模、算法求解到最终决策制定的全过程。此外，运筹学的相关理论知识如排队论、库存理论等也是解决实际问题的基础。

这张图展示了运筹学总结部分的内容，主要包括：

1. 知乎专栏：

• 专栏标题是《运筹学》，该专栏专注于人工智能、数据科学与运筹学的交叉领域。
• 访问链接：运筹学专栏。

2. 微信公众号：

• 运筹OR快嗨和ORAI-China是两个微信公众号，提供与运筹学相关的内容。
• 数据魔术师：秦虎，华中科技大学的专家。
• 运筹说：包括一些学者如徐小峰等，来自中国石油大学（华东）。
• 复杂性：胡志华，上海海事大学的学者。

通过这些渠道，大家可以深入了解运筹学的前沿进展和相关领域的研究。

专栏《运筹学》主要关注人工智能、数据科学和运筹学三者的交叉领域。它不仅探索运筹学的经典理论，还介绍如何将现代数据分析和机器学习技术应用到实际问题的优化与决策中，特别是在不确定性、复杂系统以及大规模计算方面。

专栏内容概述：

1. 运筹学与数据科学的结合：

   • 运筹学的优化算法与数据科学的统计学习、深度学习相结合，开辟了新的研究领域。专栏深入探讨了如何通过数据驱动的优化方法来解决传统运筹学中的挑战，尤其是对大规模问题、动态优化问题和非线性问题的研究。

2. 实际应用：

   • 专栏中会涉及多个行业的案例，如物流、交通、供应链管理、金融等领域。通过具体的应用实例，解释运筹学如何帮助决策者优化资源分配、提高运营效率。

3. 最新研究进展：

   • 该专栏还会跟进运筹学及其相关学科（如博弈论、排队论、网络优化等）的最新研究动态，分析运筹学领域的新技术、新工具和新的应用场景。

4. 机器学习与优化结合：

   • 特别强调机器学习与优化算法的结合，介绍了如何使用机器学习模型来增强传统优化算法的表现，尤其是在面对大量数据和复杂约束条件时的优势。

专栏受众：

• 学术界：包括运筹学、计算机科学、经济学、管理学等学科的研究人员，专栏提供了一个跨学科的视野，帮助学者们更好地理解运筹学与现代技术的融合。
• 业界从业者：特别是那些在供应链管理、物流、金融、制造业、IT和通信等领域工作的决策者和分析师，专栏提供了实用的优化模型和案例，帮助他们提高决策质量和执行效率。
• 学生和爱好者：对于运筹学、数据科学、机器学习等感兴趣的学生，专栏是一个获取知识、理论、案例的好平台。

典型话题：

• 运筹学基础理论与进展：包括线性规划、整数规划、动态规划、博弈论等经典话题的应用与发展。
• 优化方法的创新：介绍一些现代优化方法如启发式算法、遗传算法、模拟退火等，以及它们在复杂问题中的应用。
• 数据驱动的优化：如何通过大数据技术和机器学习方法，利用海量数据进行建模和优化，尤其是在不确定性环境下如何做出更好的决策。

这个专栏是一个很好的资源，适合那些希望将运筹学与现代技术结合、解决实际复杂问题的人。