单调栈、图、并查集与前缀树

单调栈

场景：

通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了。

单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素，优点是只需要遍历一次。

1、单调栈里存放的元素是什么？

单调栈里只需要存放元素的下标i就可以了，如果需要使用对应的元素，直接T[i]就可以获取。

2、单调栈里元素是递增呢？ 还是递减呢？

注意一下顺序为 从栈头到栈底的顺序

构建一个从顶部到底部单调递增的栈。

1、新元素比栈顶小，直接插入

2、新元素比栈顶大，栈出栈，直至满足1

例题

请根据每日 气温 列表，重新生成一个列表。对应位置的输出为：要想观测到更高的气温，至少需要等待的天数。如果气温在这之后都不会升高，请在该位置用 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

var dailyTemperatures = function (temperatures) {
    const n = temperatures.length;
    const res = Array(n).fill(0);
    const stack = [];  // 递增栈：用于存储元素右面第一个比他大的元素下标
    stack.push(0);
    for(let i=1;i<n;i++){
        while(temperatures[i]>temperatures[stack[stack.length-1]]&&stack.length){
            let top=stack.pop()
            res[top]=(i-top)
        }
        stack.push(i)
    }
    return res
};

---

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

• 输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
• 输出：6
• 解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

//单调栈 js数组作为栈
var trap = function(height) {
    const len = height.length;
    if(len <= 2) return 0; // 可以不加
    const st = [];// 存着下标，计算的时候用下标对应的柱子高度
    st.push(0);
    let sum = 0;
    for(let i = 1; i < len; i++){
        if(height[i] < height[st[st.length - 1]]){ // 情况一
            st.push(i);
        }
        if (height[i] == height[st[st.length - 1]]) {  // 情况二
            st.pop(); // 其实这一句可以不加，效果是一样的，但处理相同的情况的思路却变了。
            st.push(i);
        } else { // 情况三
            while (st.length !== 0 && height[i] > height[st[st.length - 1]]) { // 注意这里是while
                let mid = st[st.length - 1];
                st.pop();
                if (st.length !== 0) {
                    let h = Math.min(height[st[st.length - 1]], height[i]) - height[mid];
                    let w = i - st[st.length - 1] - 1; // 注意减一，只求中间宽度
                    sum += h * w;
                }
            }
            st.push(i);
        }
    }
    return sum;
};

 思路

首先套路固定

1、定义stack(只存储下标)

2、遍历元素（for）

3、遇见不同单调性的元素考虑运用栈顶元素和栈顶距离最新端的长度

(while（栈不为0，违反单调性）)

难点

单调性：考虑什么样的元素与结果有关，出现这样的元素时需要维护单调性。

---

图

dfs（递归）

三步骤

1、确认递归函数，参数

2、确认终止条件

        我们是处理当前访问的节点，还是处理下一个要访问的节点。这决定 终止条件怎么写。

        1、处理当前访问的节点，当前访问的节点如果是 true ，说明是访问过的节点，那就终止本层递归，如果不是true，我们就把它赋值为true

// 写法一：处理当前访问的节点
void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
    if (visited[key]) { // 本层递归是true，说明访问过，立刻返回
        return;
    }
    visited[key] = true; // 给当前遍历的节点赋值true 
    vector<int> keys = rooms[key];
    for (int key : keys) {
        // 深度优先搜索遍历
        dfs(rooms, key, visited);
    }
}

        2、处理下一层访问的节点

// 写法二：处理下一个要访问的节点
void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
    // 这里 没有终止条件，而是在 处理下一层节点的时候来判断
    vector<int> keys = rooms[key];
    for (int key : keys) { 
        if (visited[key] == false) { // 处理下一层节点，判断是否要进行递归
            visited[key] = true;
            dfs(rooms, key, visited);
        }       
    }
}

3、处理目前搜索节点出发的路径

有递归就有回溯，回溯就在递归函数的下面

BFS(队列，while循环)

无向图求最短路，广搜最为合适，广搜只要搜到了终点，那么一定是最短的路径

字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列：

• 序列中第一个单词是 beginWord 。
• 序列中最后一个单词是 endWord 。
• 每次转换只能改变一个字母。
• 转换过程中的中间单词必须是字典 wordList 中的单词。
• 给你两个单词 beginWord 和 endWord 和一个字典 wordList ，找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0。

var ladderLength = function(beginWord, endWord, wordList) {
    // 将wordList转成Set，提高查询速度
    const wordSet = new Set(wordList);
    // Set元素个数为0 或者 endWord没有在wordSet出现，直接返回0
    if (wordSet.size === 0 || !wordSet.has(endWord)) return 0;
    // 记录word是否访问过
    const visitMap = new Map();// <word, 查询到这个word路径长度>
    // 初始化队列
    const queue = [];
    queue.push(beginWord);
    // 初始化visitMap
    visitMap.set(beginWord, 1);
    
    while(queue.length !== 0){
        let word = queue.shift(); // 删除队首元素,将它的值存放在word
        let path = visitMap.get(word); // 这个word的路径长度
        for(let i = 0; i < word.length; i++){ // 遍历单词的每个字符
            for (let c = 97; c <= 122; c++) { // 对应26个字母ASCII值 从'a' 到 'z' 遍历替换
                // 拼串得到新的字符串
                let newWord = word.slice(0, i) + String.fromCharCode(c) + word.slice(i + 1);
                if(newWord === endWord) return path + 1; // 找到了end，返回path+1
                // wordSet出现了newWord，并且newWord没有被访问过
                if(wordSet.has(newWord) && !visitMap.has(newWord)) {
                    // 添加访问信息
                    visitMap.set(newWord, path + 1);
                    queue.push(newWord);
                }
            }
        }
    }
    return 0;
};

---

并查集

1.集合树：所有节点以代表节点为父节点构成的多叉树
2.节点的代表节点：可以理解为节点的父节点，从当前节点出发，可以向上找到的第一个节点
3.集合的代表节点：可以理解为根节点，意味着该集合内所有节点向上走，最终都能到达的节点
来个图帮助理解

一、首先，对于边集合edges的每个元素，我们将其看作两个节点集合

比如边[2, 3],我们将其看作节点集合2，和节点集合3

二、在没有添加边的时候，各个节点集合独立，我们需要初始化各个节点集合的代表节点为其自身

father[i]=i

即i的父节点是i

三、然后我们开始遍历边集合，将边转化为集合的关系 

找集合的代表节点（根），将根节点相连

构建集合

从节点3出发，father[3]=4, father[4]=4,于是找到节点3所在集合的代表节点为4
从节点2出发，father[2]=2, 找到节点2所在集合的代表节点为2
于是，将4的代表置为2，father[4]=2, father[2]=2
对应的father[0, 2, 2, 4, 2, 5]
对应的index [0, 1, 2, 3, 4, 5]
集合变化如下图：

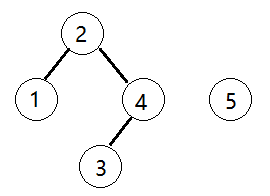
并查集可以解决什么问题呢？

主要就是集合问题，两个节点在不在一个集合，也可以将两个节点添加到一个集合中。

这里整理出我的并查集模板如下：

int n = 1005; // 节点数量3 到 1000
int father[1005];

// 并查集初始化
void init() {
    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }
}
// 并查集里寻根的过程
// 顺便更新节点
int find(int u) {
    return u == father[u] ? u : father[u] = find(father[u]);
}
// 将u-->v 这条边加入并查集
void join(int u, int v) {
    u = find(u);
    v = find(v);
    if (u == v) return ;
    father[v] = u;
}
// 判断 u 和 v是否找到同一个根
bool same(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

并查集主要有三个功能。 

1. 寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个
2. 将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
3. 判断两个节点是否在同一个集合，函数：same(int u, int v)，就是判断两个节点是不是同一个根节点

例题

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

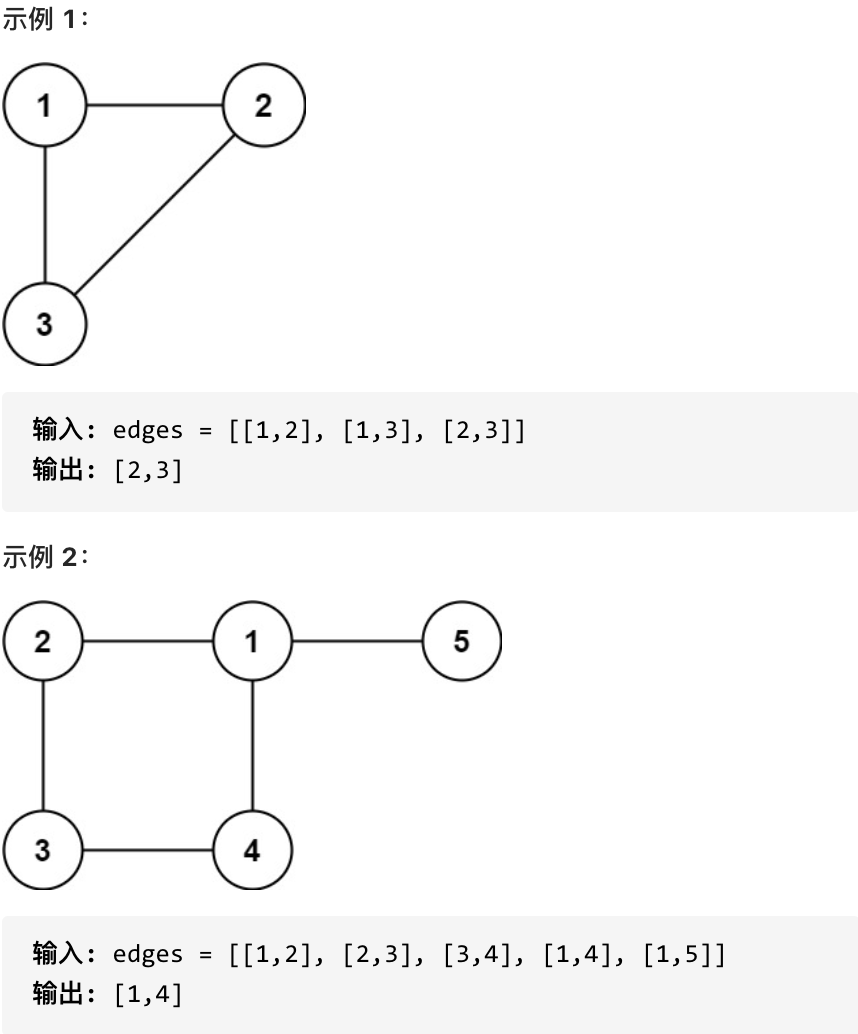
const n = 1005;
const father = new Array(n);
// 并查集里寻根的过程
const find = u => {
    return u == father[u] ? u : father[u] = find(father[u]);
};

// 将v->u 这条边加入并查集
const join = (u, v) => {
    u = find(u);
    v = find(v);
    if(u == v) return;
    father[v] = u;
};

// 判断 u 和 v是否找到同一个根，本题用不上
const same = (u, v) => {
    u = find(u);
    v = find(v);
    return u == v;
};

/**
 * @param {number[][]} edges
 * @return {number[]}
 */
var findRedundantConnection = function(edges) {
    // 并查集初始化
    for(let i = 0; i < n; i++){
        father[i] = i;
    }
    for(let i = 0; i < edges.length; i++){
        if(same(edges[i][0], edges[i][1])) return edges[i];
        else join(edges[i][0], edges[i][1]);
    }
    return null;
};

 

---

前缀树

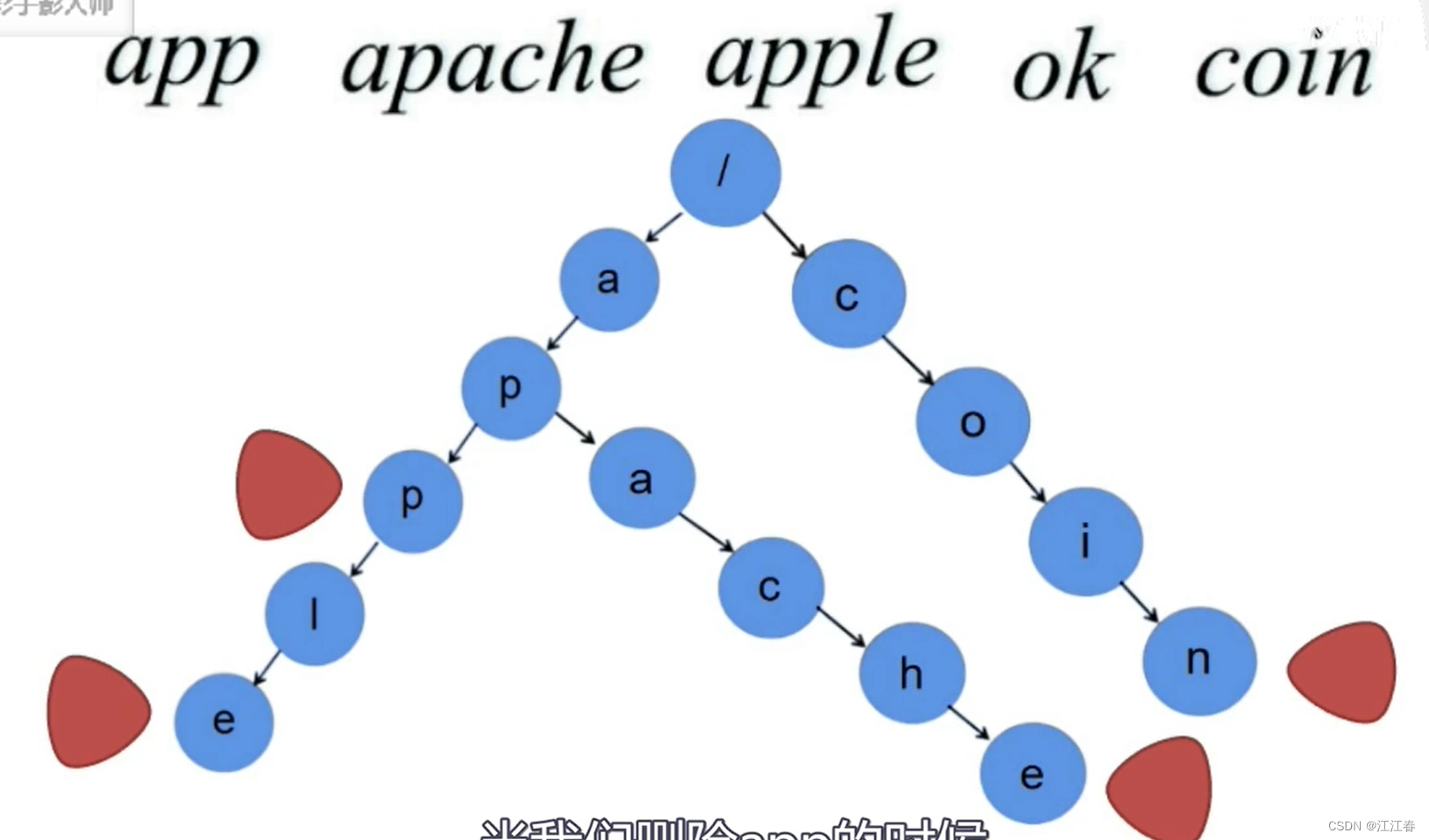
 具体来说，Trie一般支持两个操作：
1. Trie.insert(W)：第一个操作是插入操作，就是将一个字符串W加入到集合中。
2. Trie.search(S)：第二个操作是查询操作，就是查询一个字符串S是不是在集合中。

var Trie = function() {
    this.children = {};
};

Trie.prototype.insert = function(word) {
    let node = this.children;
    for (const ch of word) {
        if (!node[ch]) {
            node[ch] = {};
        }
        node = node[ch];
    }
    node.isEnd = true;
};

Trie.prototype.searchPrefix = function(prefix) {
    let node = this.children;
    for (const ch of prefix) {
        if (!node[ch]) {
            return false;
        }
        node = node[ch];
    }
    return node;
}

Trie.prototype.search = function(word) {
    const node = this.searchPrefix(word);
    return node !== undefined && node.isEnd !== undefined;
};

Trie.prototype.startsWith = function(prefix) {
    return this.searchPrefix(prefix);
};

 

---

树

满二叉树

如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

 

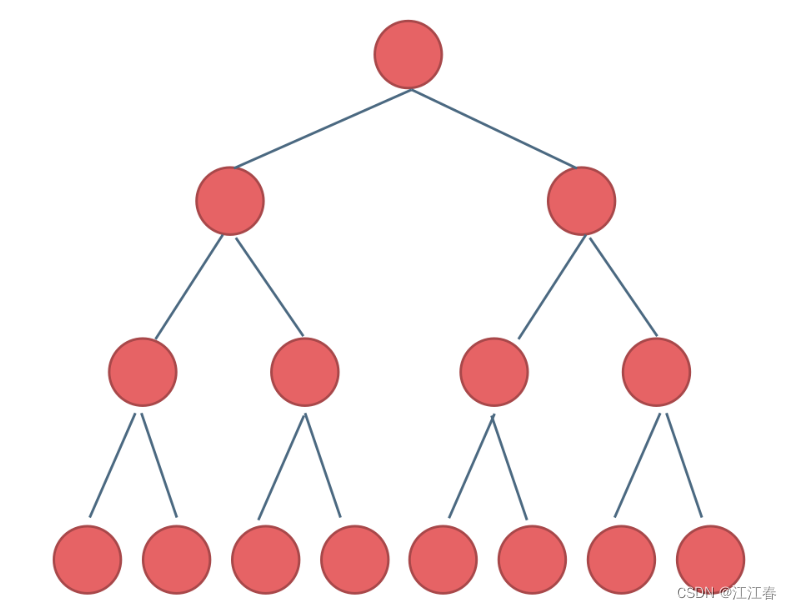
完全二叉树

在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1)  个节点。

从左到右填满

 

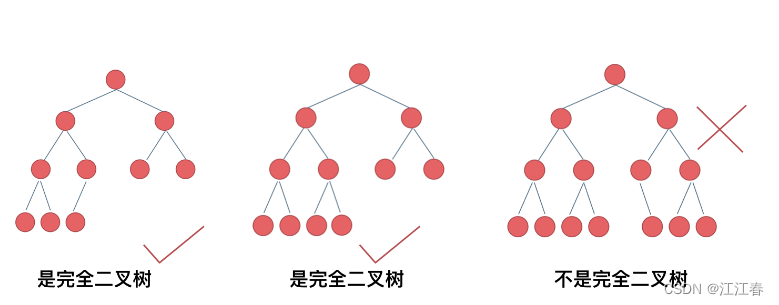
 堆就是一棵完全二叉树，同时保证父子节点的顺序关系

二叉搜索树

左小右大 

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树
• 

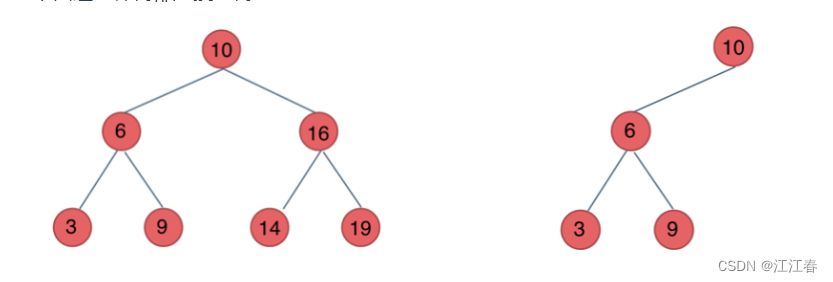
平衡二叉搜索树

 左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

 

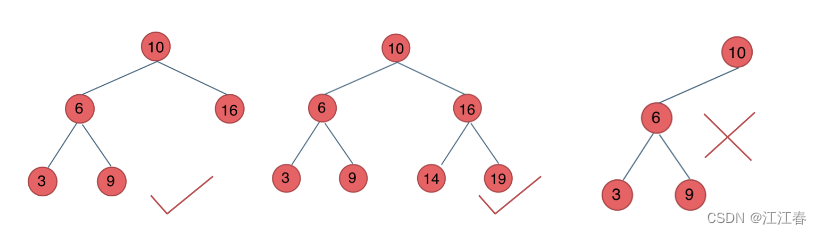
• 涉及到二叉树的构造，无论普通二叉树还是二叉搜索树一定前序，都是先构造中节点。

• 求普通二叉树的属性，一般是后序，一般要通过递归函数的返回值做计算。

• 求二叉搜索树的属性，一定是中序了，要不白瞎了有序性了。

---

时间复杂度

大O用来表示上界的，当用它作为算法的最坏情况运行时间的上界，就是对任意数据输入的运行时间的上界。 

递归算法的时间复杂度

: 递归的次数 * 每次递归中的操作次数。