【软件分析/静态分析】chapter7 课程09/10 指针分析基础（Pointer Analysis Foundations）

V 表示程序中所有变量的集合
F 表示程序中所有field的集合
O 表示程序中所有对象的集合，（因为我们allocation-sites抽象，所以这里的O对应的也是程序中创建点的集合，用 $o_{i}, o_{j}$ 来指代具体的对象）
一个instance field是由一个对象和一个field 组合起来构成的一个指针，所以它的域就是O与F的乘积，具体的instance field会用 $o_{i}.f$ 这样的来指代
Pointer表示程序中所有的指针，由两部分构成：程序中所有的变量V 和所有的instance fields。

有了这些域，就可以表示指向关系，用 $pt$ 来表示，pt 本身是个映射(key是指针-value是相应的对象的集合)，指针集就是把具体的指针Pointer→对象集合的映射，P(O)表示O的幂集，用pt(p)表示变量p的points-to集合（指针集/指针域）

7.1.2 Rules 规则

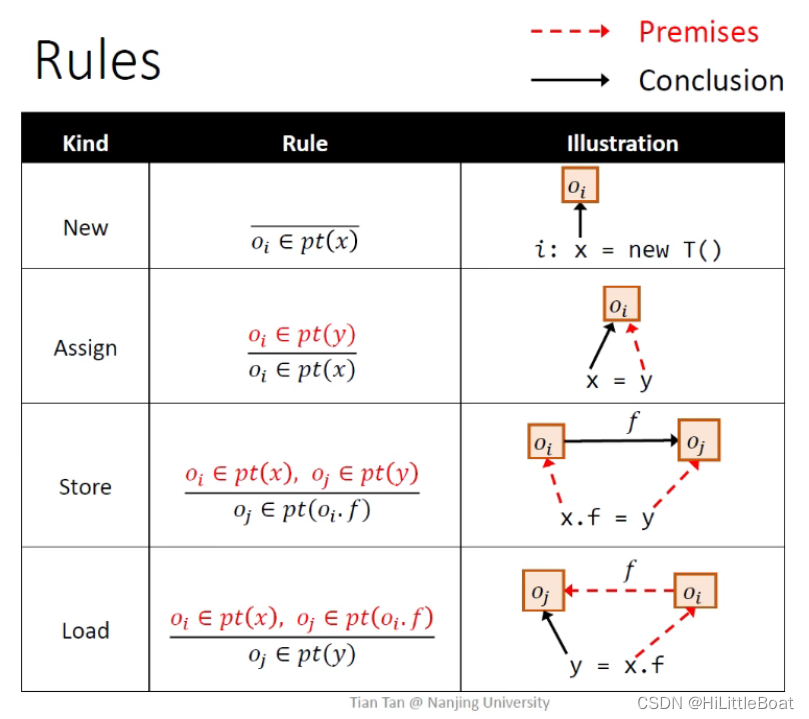
下表就是处理四种语句的规则，横线上边表示前提条件premises，下边是结论conclusion，对于某个语句，如果前提条件满足，就能推导出结论。对于第一条语句比较特殊，是无条件的unconditional：

1. New语句的规则

如图所示，i 表示代码所在位置，oi 表示allocation-sites，也表示在这一点创建出来的对象。

new语句右侧没有指针域，所以没有前提条件，直接得出结论。指针分析对于new语句需要做的就是，让x 指向 oi，图中的实线箭头表示这条规则产生的新的指向关系即x→oi，即规则中的oi∈pt(x)，将这条语句new T对应的对象oi 加入变量x 的指针集pt(x)中。

2. Assign语句的规则

对于赋值语句，例如x=y，就是，y指向什么，就让x指向什么。做指针分析的时候就是把y指向的东西加入到x中。

如图所示，如果已知 y指向oi，那么指针分析就让x也指向oi。

3. Store语句的规则

store语句的语义：如果x指向某个对象oi，y指向另一个对象oj，需要让oi的field f 指向oj。

指针分析要做的就是，如果满足两个前提条件条件，就把oj加入到oi.f的指针集中。

4. Load语句的规则

与store类似，这里是取x.f的数据，将等号右侧的对象x的field f的指针集的数据oj加载到等号左侧的y的指针集中。

5. 总结

7.2 如何实现指针分析

7.2.1 实现的关键

本质上，指针分析是将points-to信息（指向信息）传播到由variable & fields组成的指针之间的过程。指针分析可以看作是一系列的指针之间的包含约束（inclusion constraints）。例如说x=y，就可以看作，指针x包含指针y的所有对象的信息。指针分析就是根据这一系列的约束，进行求解，解出最后一个结果可以满足这一系列约束的包含关系。

要实现指针分析的关键：当指针x的指针集pt(x)发生改变的时候，要把改变的部分传播给与x相关的指针。

处理问题的方式：用图去连接相关指针；当一个pt(x)发生变化的时候，将变化的部分传播给x的后继。

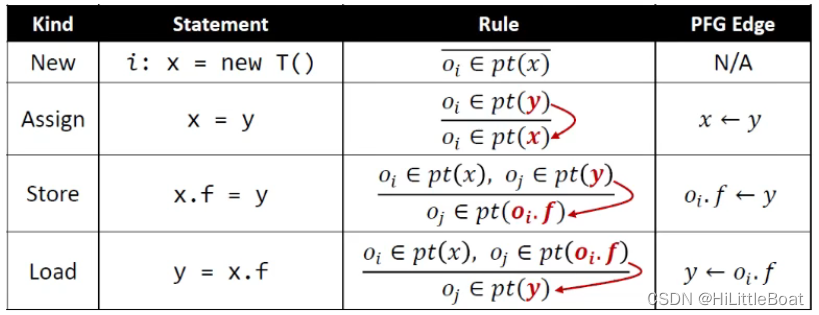
7.2.2 指针流图（Pointer Flow Graph, PFG）

程序的指针流图是一个有向图(directed graph)，它表示程序中的对象在指针之间是如何流动的。由边和节点组成：

Nodes 节点： Pointer = V ∪ (O × F)
节点n 代表一个variable 或者一个抽象对象的field
Edges 边：Pointer × Pointer
边 x → y 代表意味着指针x指向的对象可能流向指针y指向的对象，可以理解为 y = x ⇒ x → y ⇒ pt(x) ∈ pt(y)

PFG的边是根据程序中的语句、处理指针分析的规则建立的，如下图所示，PFG的边就是画出来的几条边：

7.2.3 一个例子🌰

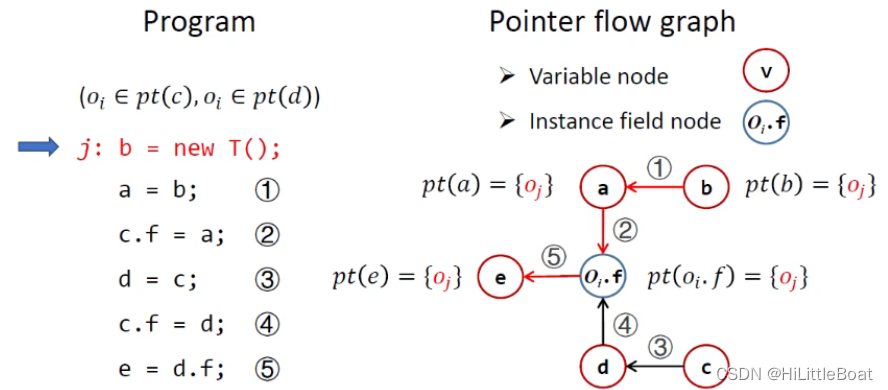
接下来，我们通过一个例子感受一下PFG是怎么绘制。如下图所示，对左边的程序，建立PFG，这里有两种node：variable node 和 instance field node，

此程序有个前提假设，就是c和d都指向oi（c指向oi说明oi肯定在c的指针集中，但是c的指针集中可能还有别的），也就是说二者是利用同一个类创建的对象。第一句和第二句可以画出两条边，代表b流向a，a流向 c.f 即 oi.f ；同理第三句第四句可以划出下面的两条边，代表c流向d，d流向 c.f 即 oi.f ；第五句代表 d.f 流向e，又因为前提条件中c和d都指向oi，所以得到第五条边。

上段内容参考博主童年梦的笔记：【软件分析/静态程序分析学习笔记】8.指针分析基础知识(Pointer Analysis Foundations)_童年梦的博客-CSDN博客

有了PFG，指针分析的问题就可以变成在PFG上求传递闭包（transitive closure）的问题。

例如PFG中的指针e可以从b可达，意味着b所指向的对象 may flow to 并被e所指向。假如加一条语句 j: b=new T()，也就是说这条语句创建的对象b的指针集里包含oj，接下来我们就根据这个图传递指向关系，oj可以从b 传播到 a 再传播到 oi.f 最后传播到e，如下图所示。

由上述过程，可以总结出指针分析主要有两个过程，① 画指针流图PFG；②在指针流图中传播指向信息，这两个过程相互依赖着动态进行的。例如在画第五条边的时候就需要前面的指向信息才能画出。

7.3 指针分析的算法⭐

7.3.1 算法总体

如下图所示为整个算法。

这里涉及到三个结构：

输入S：要分析的程序的语句的集合
WL：work list，存放有待处理的指向信息，
PFG：指针流图，在算法中表示为边的集合

其中WL 存放了一系列的指向信息，表示为 𝑊𝐿 ⊆ <Pointer, 𝒫(O)>，也就是一系列的<指针，指针集> 的列表，例如 [<𝑥, {𝑜𝑖}> , <𝑦, {𝑜𝑗, 𝑜𝑘}> , <𝑜𝑗.𝑓, {𝑜𝑙} >…] 的形式。

7.3.2 初始化——处理New 和 Assign语句

如下图所示，为初始化阶段核心代码，可以分为3个步骤：

1. 将 WL和 PFG初始化为空

2. 循环处理New语句

遍历所有new语句，然后根据规则，将每个指针与对应的域绑定传入WL中；

3. 循环处理Assign语句

遍历所有assign语句，然后根据规则，例如代码 x=y，需要增加 y→x 的边，这里需要调用📞AddEdges(y, x)函数来进行加边操作，addEdeges(s,t)函数见7.3.3

7.3.3 AddEdge(s, t) 用于加边的函数

这个函数的作用就是往PFG里加一条边( s 表示source; t 表示 target; 即赋值语句 t=s，就是要将s的指针域流向t，边就是s→t )具体过程如下：
① 如果 s→t 在PFG中已经存在，就什么都不用做
② 如果 s→t 不存在，则增加 s→t 到PFG：
③ 加完边之后，如果 s 的指针域pt(s)不为空，则需要将<t, pt(s)>加入WL（为了保证s指向的对象，t也可以指向）

注意，y→x 并不是指向的意思，而是流向，意思就是说y指向的指针集，可以流向x指向的指针集，想要保证这一点，就需要将pt(y)里的对象与 x组成一个对，放入WL中，在后续处理。

7.3.4 主体部分Ⅰ——差分传播

在初始化完成后，算法会循环处理WL中的对pair，直到WL为空，循环停止。循环内部主要做了如下步骤，其中2和3步就是重要的差分传播：

1. 从WL中取出来一对pair <n, pts>

2. 取pts和pt(n)的差集，即去除pts中所有已经存在于n指针域中的指向信息，得到Δ；例如：

3. 再对n和Δ做一个📞 Propagate 传播操作，调用Propagate(n, pts)函数如下所示：

① 如果pts 为空，就不做任何操作；
② 如果pts 不为空，则将传入的指针域pts 加入n的指针域，⭐
③ 然后将 pst 与 n的所有后继s 构成对pair，加入WL中。⭐

结合之前的Δ，传播的过程可以理解为，将n缺少的指向信息加入n的指针域中，然后将这变化部分传播给n的后继。算法中pt(n) ⋃= pts 也是整个算法里唯一一处改变指针集的地方。
Insight: 之所以需要做差分，也是为了进行去重，避免冗余操作，减少系统开支。pt(n) 中已有的指向信息已经传播到n的继承者，这些信息不需要再被传播。

7.3.5 主体部分Ⅱ——处理Store 和 Load语句

在初始化的时候，已经将所有的New语句和Assign语句处理过了，此时只有Store和Load语句需要分析。

这部分代码仍是在work list不为空的循环体内。在从WL中取出一个对<n, pts>并进行差分传播过程后，如果 n 是一个变量，则查看所有在Δ中的指向信息，然后在程序语句中找到与这个变量有关的 n.f 然后进行对应的7.3.3中的 AddEdge操作。（为什么是查看Δ呢？因为这里的对象是真正x之前没有指向的对象，也就是需要我们进行处理的。）

新的指向信息可能会引入新的边。（为什么说可能呢？因为，例如说处理x.f=y 的时候，产生的新的指向关系是y→oi.f，但是程序中可能有另外一句话，a.f=y，且a也指向oi，所以这个边可能已经连上了）

7.3.6 总结

以上便是整个指针分析的算法，首先对整个程序语句进行分析，用其中的New语句和Assign语句进行初始化，得到一个部分的PFG，然后利用WL的迭代反复补充指向关系和流向关系，完善PFG中的边和节点的指向信息。代码的模块拆分版如下图所示，干净纯享版在7.3.1中。

7.3.7 举个栗子🌰

因为是流不敏感的分析，所以最开始，是把这7条语句作为一个集合S传给算法中，并不区分算法的先后顺序。

初始化：接下来先遍历程序中的new语句，放入WL中。再处理赋值语句，往PFG中加边（AddEdge核心有两步：一个是加边，另一个是把等号右边的变量的指针域，给左边的变量，例如说a=b，就是要把<a, pt(b)>加入WL，让后续处理，但是因为此时b的指针域是空的，所以没有执行AddEdge的第二步）此时 WL中有new语句放进来的待处理信息，PFG中有赋值语句增加进来的两条边（每个节点旁边的{}中会记录该节点的指针域），如下图所示：

然后就进入WL队列啦，先取出来一个对<b, {o1}>，执行差分传播以及处理有关b的store和load语句（没有与b有关的store和load语句，所以这个只执行差分传播）：

差分传播：因为pt(b)本来是空集，所以Δ仍是{o1}，再进行Propagate操作（其核心也是两步：先将传入的指针集pts即{o1} 加入自己的指针集pt(b)，然后再让该指针域能传入其后继节点：将 pst 即{o1}与 b的所有后继a 构成对pair即<a, {o1}>，加入WL中）

由于程序中没有与b有关的store和load语句，所以关于<b,{o1}>的处理结束，再从WL中取出下一个pair <c,{o3}>，在执行差分传播和处理有关c的store和load语句：

差分传播：同理，因为pt(c)本来是空集，所以Δ仍是{o3}，再进行Propagate操作：先将传入的指针域pts即{o3} 加入自己的指针集pt(c)里，然后将 pst 即{o3}与 c的所有后继d 构成对pair即<d, {o3}>，加入WL中。

处理有关c的store和load语句：（需要找到Δ里的每一个oi，分别对这每条store和load语句进行加边（加边的主要操作：图里添加边，并把等号右边的变量的指针域，给左边的变量（通过加入WL的方式））这里即第4和6行的c.f相关的store语句，且Δ为{o3}，所以是执行AddEdge(a,o3.f),和AddEdge(d,o3.f)，具体加边操作是：先在PFG中加边a → o3.f ，并将a的指针域赋值给o3.f（这里a的指针域为空，所以忽略）；同理，在PFG中加边d → o3.f ，并将d的指针域赋值给o3.f（这里d的指针域为空，所以忽略）。所以这个操作总共是加了两条边。

再从WL中取出下一个pair <a,{o1}>，在执行差分传播和处理有关a的store和load语句：

差分传播：pt(a)为空，没有o1，Δ={o1}，再执行propagate(a, {o1})，即①将o1放入自己的指针域pt(a)，②将{o1}与a的后继节点形成对，加入WL，即<o3.f, {o1}>加入 WL。

处理有关a的store和load语句：无

再从WL中取出下一个pair <d, {o3}>，在执行差分传播和处理有关d的store和load语句：

差分传播：d的域中没有o3，所以Δ仍={o3}，再执行propagate(d, {o3})，即①将o2放入d的指针域pt(d)，②再将o3与d的后继o3.f，构成对<o3.f, {o3}>，加入WL

处理有关d的store和load语句：即第7句e=d.f，然后对Δ{o3}的每个值o3，形成o3.f，与e一起进行加边操作AddEdge(o3.f, e)，即①PFG上加边o3.f→e，②把等号右边的变量的指针域，给左边的变量，形成对，加入WL，等号右边的变量的指针域为空，所以不执行这步操作。

再从WL中取出下一个pair <o3.f, {o1}>，执行差分传播和处理有关o3.f的store和load语句：

差分传播：o3.f 的指针域中没有o1，所以Δ仍为{o1}，再执行propagate(o3.f, {o1})，即①将o1放入o3.f的指针域pt(o3.f)，②再将o1与o3.f的后继e，构成对<e, {o1}>，加入WL。

        处理有关o3.f的store和load语句：无。

        再从WL中取出下一个pair <o3.f, {o3}>，执行差分传播和处理有关o3.f的store和load语句，同理，这里不再赘述，简单介绍变化：差分传播时候①将o3放入o3.f的指针域pt(o3.f)，②再将o3与o3.f的后继e，构成对<e, {o3}>，加入WL。

最后只剩的两个有关e的操作，就比较简单了，不再详细介绍，因为e没有后继，也没有store和load语句，所以就是把o1，o3 都加入e的指针域即可，也不会有新的对加入WL。

至此，算法结束，得到的PFG如上图所示。

7.4 指针分析如何处理方法调用

7.4.1 方法调用时的指针分析

1. 过程间指针分析需要调用图

如果程序中有方法调用，那我们的程序分析就是过程间的，需要call graph。例如下边的程序，如果我们想知道pt(a)，就需要知道谁调用了foo方法，才可以知道把什么参数传给了a，同理，要算pt(b)也需要知道谁调用的bar()方法，返回值是什么。

void foo(A a){ //pt(a) = ??
    ...
    b = a.bar(); //pt(b)=??
    ...
}

2. CHA vs 指针分析

回顾第5章，CHA方法可以用来解call graph，对比指针分析，针对上述代码，对比如下：

CHA：基于 a的声明类型A 来处理调用信息，不精确，会引入虚假的调用边和指向关系。
Pointer analysis：基于 a的指针域pt(a) 来处理调用信息，比较精确，因为用指针分析构造call graph，所以同时考虑到调用图和指向关系。

利用指针分析构建call graph，实际是在指针分析的过程中做call graph，我们称这种方式为 on-the-fly call graph construction。

在这节课中，不仅会学习指针分析如何处理方法调用，还会学到如何用指针分析做过程间分析。

7.4.2 Rule 规则

1. 调用语句的规则

针对如下调用语句，规则如上图所示，有3个前提→3个结论，主要完成4件事情，用到了4个符号，并连接了2种边。

l: r = x.k(a1,...,an) //x为变量，k为调用的函数名称（方法签名），a1~an为n个参数

① 指针分析处理调用的时候一般负责如下4件事情：

dispatch → 传递receive objects → 传参数 → 传返回值

② 解释一下规则中用到的4个符号：

Dispatch(oi, k)：根据oi的类型(即实例对象x的类型)和 k(调用点上的方法签名)，解析出实际的目标方法
- 解的过程与CHA的dispatch作用相同，就看oi对应的类型有没有k方法，没有继续在该类型的父类里去找，直到找到这个真正的目标方法为止）
- 在规则中就是解析为目标方法后赋予给 m，然后才有后续的定义）
：目标方法m 的 this 变量
- 传this，如图中的虚线箭头，将x指向的oi 传递给m_this 的指针域，但是这个是不建边的
：目标方法m 的第 j 个parameter(参数)
- 为了方便传参，实参→形参，会用边连起来
：目标方法m 的返回值
- 如果一个对象ov属于目标方法的m_ret指向的对象，拿就需要让调用的对象r也可以指向ov，即程序中，ret指向的对象，也要让r可以指向，返回值→变量，会用边连起来，如图红色箭头

③ 再来解释一下规则：

为什么 x 到 this，不建立边呢？因为对于一个类里的this而言，直指向自己，而如果从x到this有一条边，那么x里的所有指向都会给这个this，从而产生错误指向，如下图所示：

所以实际的做法，不把这条边连上，我们就老老实实地根据规则，pi∈pt(m_this)，把oi传给相应的this，而不是通过边流过去。

7.4.3 算法

1. 整体算法

上图即整个算法，其中黄底的代码是相对7.3的算法新增的部分。

算法的输入有所改变：之前算法的输入是所有语句的集合S，这里的算法的输入是 $m^{entry}$ 即输入程序的入口方法（即main方法）。这样的话，每次操作只分析从当前处可以到达的方法，可以有效地减少分析时间，提高分析精度。

2. 初始化

（1）初始化的数据结构：

WL：work list 同7.3
PFG：指针流图，同7.3
S：可达的语句（reachable statements）的集合，初始化为空
- $S_{m}$ ：方法m的语句的集合
RM：可达的方法的（reachable methods）集合，初始化为空
CG：调用图的边，初始化为空

（2） 对于入口节点添加可达性方法，AddReachable( $m^{entry}$ )，具体

3. AddReachable(m) 添加可达性方法

如上图所示，即AddReachable(m)的代码，传入的参数为一个方法m，首先判断 m 是不是已经在RM 的集合里，如果已经存在，则不对m做处理，如果不存在，说明是个新方法：
① 将这个方法 m 加入RM，并将其语句的集合 Sm 加入所有可达的语句的集合 S
② 对新发现的语句更新WL和PFG：
Ⅰ. New 语句：<x, {oi}> 加入WL
Ⅱ. 赋值语句：加边AddEdge(y,x)，这里的函数同7.3.3 的函数（AddEdge核心有两步：一个是加边，另一个是把等号右边的变量的指针域，给左边的变量，例如说x=y，就是要把<x, pt(y)>加入WL）

这个函数会在两个时候被用到：

算法一开始的时候的入口函数，会被调用，以找到其可达性节点
当新调用边被发现的时候

为什么在这里只处理了new 和赋值语句，没有处理store 和 load语句呢？

对于store 和 load语句，例如说 x.f = y，需要根据x的指向信息才能进行处理。如果是刚刚加进来的新方法，方法里的对象x的指向信息还是空的，无法处理store和load语句。
对于new 和赋值语句，不需要知道他们的指向信息，只通过语句本身，就可以进行处理
等后续 x 发生变化的时候，在大循环中，自然会处理，为了做到这一点，所以有一个操作就是：初始化的时候将所有与m相关的语句都加入S里边，以便后续处理

4. 主体部分Ⅰ Ⅱ：差分传播和处理store & load 语句

上图中红色框框内为算法的主体部分，除了最后一句，前边的都与7.3 的主体部分一致。

循环体内，主要完成的工作是：
Ⅰ 从WL中取出来一对pair，然后把这个pair的指针集做一个差集，得到Δ，然后进行传播
Ⅱ 如果 pair里的变量涉及到 store 和 load 语句，就再处理一下加边操作
Ⅲ 如果 pair里的变量涉及到方法调用，就调用ProcessCall，进行处理

在第Ⅰ步中计算了Δ，这里边的对象对于取出来的pair中的指针n 而言都是新的，都是n的指针域里没有的，我们需要对这些新的对象做一系列操作（处理store、load、call）。

前两步骤同 7.3.4 和7.3.5 这里不再赘述，第Ⅲ步的主要内容如下：

5. 主体部分Ⅲ：处理call语句 ProcessCall(x, oi)

处理call语句，主要通过 ProcessCall(x, oi)函数来实现，根据7.4.2中的call语句的规则，传入了两个参数，调用者x，和流入调用者的新对象oi。就像7.4.2中所讲的，首先取出来所有有关x的调用语句：
① 对于每个调用语句，先通过Dispatch函数，解出目标方法（被调用的方法）赋给m（Dispatch函数的实现，见第五章的笔记，5.2.4，这里的dispatch 不会直接根据声明类型，而是根据其声明语句时候的 new）
② 然后将<m_this, {oi}>加入WorkList中（在后续处理的时候，就会把receiver object 传递给 this 变量）
③ 接下来检测 l → m 这个边是否已经在CG中，如果不在就加入，然后对这个m进行AddReachable操作，④ 并将对应的参数和返回值用边相连。(因为这个语句可能在处理同方法的时候已经连接过了，所以要判断一下是否在CG中)

7.4.4 举个例子🌰

左图为算法的主要代码，接下来，将对右图的代码进行分析：

初始化：将WL,PFG,S,RM,CG都置为空，其中RM存放待处理的函数，S存放待处理的函数里的方法（这个省略了，就不展示了）

处理可达的方法和语句 AddReachable（这个方法的主要步骤是：如果这个方法不在RM中，则加入RM，再将这个方法里的语句加入S，并对S中的new和赋值语句进行处理，更新WL和PFG）：将main节点传入这个函数，进行处理，首先main方法还不在RM中，证明没被处理过，则将main 加入RM，再main的语句(line 3-5)都加入S，然后处理main里的new语句和赋值语句，这里只有两个new语句即line3、4，则分别将<a, {o3}>,<b, {o4}>加入WL，


   然后就进入WL队列啦，先取出来一个对<a, {o3}>，执行差分传播以及处理有关b的store和load和call语句，差分传播就不再详细写了，且a没有load、store、call语句，所以直接跳过。

再取出来下一个对<b, {o4}>，执行差分传播后如下：

b没有相应的store和load语句，有call语句第5行，则对Δ里的每一个对象执行ProcessCall命令，即执行ProcessCall(b, o4)：

① 先通过Dispatch(o4, foo) 解目标方法，根据o4是 new B，则在B方法里找，有foo方法，则返回B.foo，存入m中，即m=B.foo(A)
② 传this：将<B.foo_this, {o4}>传入ML
③ 建立CG，增加可达的方法：这里我们拿行号作为label，即将 5→B.foo(A) 加入CG（如果是CHA方法，在前边Dispatch 的时候，会根据b的声明类型A来找，就会多一个A.foo，导致假边），然后对这个新方法B.foo(A) 进行AddReachable操作（这个方法的主要步骤是：如果这个方法不在RM中，则加入RM，再将这个方法里的语句加入S，并对S中的new和赋值语句进行处理，更新WL和PFG）这里涉及到一个new语句，即把<r,{o11}>加入WL
④ 传参，传返回值：要对每个参数和返回值执行AddEdge()操作（加边，更新WL），这里就是传参的时候加边：a→y；然后把对应的a的指针域与y形成对<y,{o3}>加入WL；传返回值的时候加边：r→c；然后因为r的指针域还是空的，所以不用往WL里加对。

剩下的WL中的三个对，同理，就不复杂了，他们三个都不涉及store、load、call语句，所以只进行差分传播即可，这里不再详细写了。算法最终结果如下图所示：

至此分析完成！

经过上述的关于指针分析的例子，感觉清晰多了，但是依然还有一点点问题，例如：

1. 形参y，以及函数里的返回值r是否需要标记是某个函数的？

2. 变量名如果有重复怎么办，一般是不是得带上方法名？

3. PFG能否与CG放在一起？

4. 如何从变量，再去获取当前函数信息、类信息？函数信息可能可以直接从RM取出来，存一下，那类的信息怎么保存？

这个例子中没有涉及到store、load、赋值语句，所以画出来的图也不是特别复杂，大致过程是理解了，但是关于实现的细节，为什么这样实现，以及从整体架构上把握还有待进一步的实践和回顾。希望能够与各路大佬或初学者一起探索。