基于EasyX学习图形学中的二维几何变换——旋转

Lose&recall

已于 2024-07-04 10:15:29 修改

阅读量3.1k

点赞数 8

分类专栏：图形学文章标签：学习几何学 c++ 算法

于 2022-05-17 12:34:08 首次发布

本文链接：https://blog.csdn.net/qq_46820097/article/details/124805079

版权

图形学专栏收录该内容

7 篇文章

订阅专栏

本文介绍了在图形学中如何通过旋转矩阵实现二维图形的旋转，详细讲解了旋转原理、核心代码示例，并展示了使用EasyX库进行线条旋转的实战过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

几何变换系列文章目录

easyx实现图形学中的二维变换——平移

前言

之前发布过学习图形学中的平移，这次学习图形学中的旋转，旋转相对较麻烦些，但道理基本一致

一、旋转的变换方法？

旋转变换是基于原点进行旋转的，而原先的角度则是和X轴的夹角α，规定逆时针旋转的角度为正值，所以当旋转了一个角度β后，和X轴的夹角则变成α+β，如下图所示
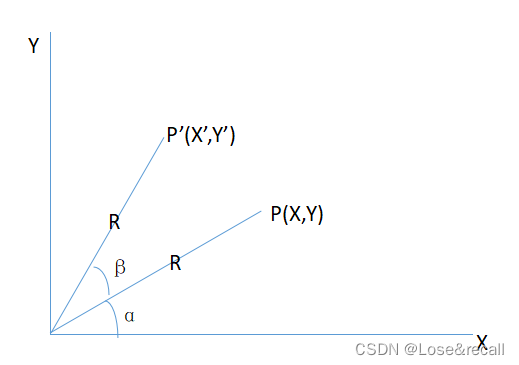
根据点的极坐标表示法可以知道原先的P点的极坐标表示为X=Rcosα，Y=Rsinα,而旋转后变为X’=Rcos(α+β),Y’=Rsin(α+β)，根据三角函数公式cos(a＋b)＝cosacosb－sinasinb，sin(a+b)=sinacosb+sinbcos a，便可以推断出X’=Xcosβ-Ysinβ，Y’=Xsinβ+Ycosβ便可以将其表示为矩阵乘法
从图中便可以看出二维旋转变换矩阵为

由此可以看出只需要有个旋转角度便可以进行旋转，当顺时针旋转时，角度变为负数，此时sin会变化，可以算出顺时针的旋转矩阵
在实际应用中可能会存在不是绕原点旋转，此时就需要借助平移将参考点移动到原点然后旋转完后再平移至原地方

二、核心代码

//前面的代码可以参考上一节平移中的代码
//此处只展示了旋转部分代码
void E_Transform::E_Rotate(double thet)
{
	Identity();
	T[0][0] = cos(thet); T[0][1] = -sin(thet);
	T[1][0] = sin(thet); T[1][1] = cos(thet);
	MultiplyMatrix();
}

//主函数调用测试（线条的旋转）
	HWND hwnd = initgraph(500, 500);
	setbkcolor(WHITE);
	cleardevice();
	setlinecolor(LIGHTBLUE);
	setlinestyle(PS_SOLID, 2);
	setorigin(250, 250);//重新设置原点
	setaspectratio(1, -1);//重新设置y轴方向
	E_Point P[2] = {
		{0,0},
		{200,200}
	};
	E_Transform Rorate;
	Rorate.SetMatrix(P, 2);
	for (; 1;) {
		moveto(P[0].x, P[0].y);
		lineto(P[1].x, P[1].y);
		Rorate.E_Rotate(PI / 6);
		
		Sleep(1000);
		cleardevice();
	}
	closegraph();
	return 0;