Dijkstra和Floyd算法

Dijkstra和Floyd算法

Dijkstra算法

Dijkstra算法用于求解从图的一个点出发到任意一个点的最短距离的算法，他可用于求解正权图中的最短路径算法，不能够用于求解负权图，时间复杂度为O(n^2)

• 算法思路

构建三个集合，一个初始集合S，一个待求解集合U，一个距离集合W

• S集合存放已经找到最短路径的节点
• U存放还未找到最短路径的节点
• W中存放从起始节点出发到各个节点的最短路径的集合

具体思路

1. 假设有a,b,c,d,e五个节点，从a节点出发寻找到b,c,d,e各个节点最短的节点，起始S = {a},U = {b,c,d,e},W = {INF,INF,INF,INF,INF},INF为无穷大不可到达，首先需要初始化W，遍历b,c,d,e节点，如果a节点能直接到对应位置，则更新W对应位置，否则为INF

2. 然后从U中找出一个据a点最短的路径节点，假定为b,此时：S = S + b, U = U - b

3. 然后遍历W的每一个位置，如果W(a,i) > W(a,b) + dir(b,i),dir为b到i的距离，W(a,i) = W(a,b) + dir(b,i)

4. 然后冲入2，3的操作，直到U集合为空，此时得到的W集合为从a出发的到其它节点的最短路径

伪代码为:

INIT SET S, U, W
while(U非空)
    FIND MIN DIR NODE FORM U WHICH IS CALLED node
    S = S + node
    U = U - node
    FOR W
     if W(a, i) < W(a, node) + DIR(node, i)
         W(a, i) = W(a, node) + DIR(node, i)
END

比如说下面有一个图

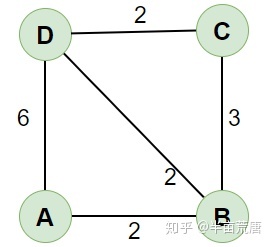
从A出发寻找A到BCD的最短路径的过程为

首先初始化S={a},U={b,c,d},W={0,2,INF,6}

从U中寻找到据a最短的那个节点,发现为b,此时S={a,b},U={c,d}

遍历W,更新W,此时
$$\begin{gathered} W(a,a)=0 \\ W(a,b)=2 \\ W(a,c)=5 \\ W(a,d)=4 \end{gathered}$$
第一个操作之后S={a,b},U={c,d},W={0,2,5,4}

再次从U中找出一个据a最小的节点，为d,此时S={a,b,d},U={c}

遍历W,更新W,此时
$$\begin{gathered} W(a,a)=0 \\ W(a,b)=2 \\ W(a,c)=5 \\ W(a,d)=4 \end{gathered}$$
然后又是同样的操作，最终得到的集合为S={a,b,c,d},U={},W={0,2,5,4}

算法代码为

假定有下面的一个图，从中寻找从节点1出发到其他节点的最短路径

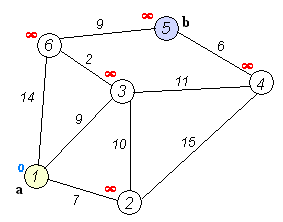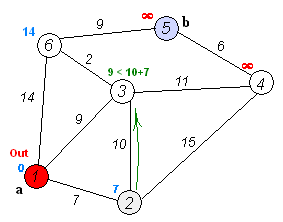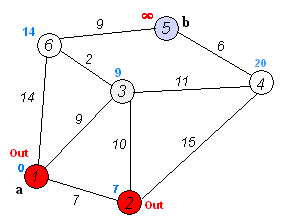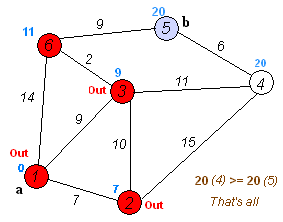
邻接矩阵为

	1	2	3	4	5	6
1	0	7	9	0	0	14
2	7	0	10	15	0	0
3	9	10	0	11	0	2
4	0	15	11	0	6	0
5	0	0	0	7	0	9
6	14	0	2	0	9	0

import numpy as np

graph_matrix = np.array([[0, 7, 9, 0, 0, 14],
                        [7, 0, 10, 15, 0, 0],
                        [9, 10, 0, 11, 0, 2],
                        [0, 15, 11, 0, 6, 0],
                        [0, 0, 0, 7, 0, 9],
                        [14, 0, 2, 0, 9, 0]])


def Dijkstra(matrix, s_node, nodenums):
    """
    Dijkstra算法
    matrix: 邻接矩阵
    s_node: 起始节点
    nodenums: 节点总数
    -1代表无穷大
    """

    # 初始化S,U,W集合
    S = [s_node]
    U = [node for node in range(nodenums) if node != s_node]
    W = []
    for idx in range(nodenums):
        if idx == s_node:
            W.append(0)
        else:
            if matrix[s_node][idx] != 0:
                W.append(matrix[s_node][idx])
            else:
                W.append(-1)

    # 开始进入算法流程
    while len(U) != 0:
        # 从U中寻找距离s_node距离最小的节点
        min_dir_idx = U[0]
        min_dir = W[min_dir_idx]
        for idx in U:
            if W[idx] != -1 and W[idx] < min_dir:
                min_dir = W[idx]
                min_dir_idx = idx
        # U = U - node, S = S + node
        U.remove(min_dir_idx)
        S.append(min_dir_idx)
        if min_dir == -1:
            continue
        # 遍历W，更新W
        for idx in range(nodenums):
            if idx != s_node:
                # if W[id] > W[n] + dir(n, id)
                # W[id] = W[n] + dir(n, id)
                if matrix[min_dir_idx][idx] != 0:
                    if W[idx] == -1:
                        W[idx] = min_dir + matrix[min_dir_idx][idx]
                    else:
                        W[idx] = min_dir + matrix[min_dir_idx][idx] if W[idx] > min_dir + matrix[min_dir_idx][idx] else W[idx]
    # Print the result
    for idx in range(nodenums):
        print(f"Form Node{s_node+1} to Node{idx+1} Min Dir is: {W[idx]}")
    # End


Dijkstra(graph_matrix, 0, 6)

输出结果

Form Node1 to Node1 Min Dir is: 0
Form Node1 to Node2 Min Dir is: 7
Form Node1 to Node3 Min Dir is: 9
Form Node1 to Node4 Min Dir is: 20
Form Node1 to Node5 Min Dir is: 20
Form Node1 to Node6 Min Dir is: 11

Floyd算法

Floyd算法能计算任意两点之间的最短路径，其时间复杂度为O(n^3),关键是它可以理解为n次Dijkstra算法