算法设计知识点及易错习题

最新推荐文章于 2022-09-27 15:03:43 发布
最新推荐文章于 2022-09-27 15:03:43 发布
阅读量545 收藏 8
点赞数 1
分类专栏： 算法 文章标签： 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_48566899/article/details/122023095
版权

时间复杂度

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
为防止递归的无休止调用，在递归函数中要及时返回，这就是结束条件的作用。我们应当看到，在所有的递归函数中都有一个终止递归的条件判断在这里插入图片描述
斐波纳契数列的递推式为：

F(n)=     1          n=1 || n=2
       F(n-1)+F(n-2)   n>2

<1>从数学上讲，上面式子与下面式子等价

  F(n)=     1           n=1 || n=2
         F(n+1) - F(n-1)   n>2

但是我们能写成下面的递归函数吗？

int f(int n)
{
   if(n==1 || n==2) return 1;
   else return f(n+1)-f(n-1);
}//分析函数异常的原因。

简要分析，按上面递归式展开，有：

F(n)=   F(n+1)    -   F(n-1)
     =[F(n+2)-F(n)]-[F(n)-F(n-2)]

也就是说F(n)在递归展开后，又重新回到了F(n)，这样导致永远无法递归退出。暂时我们可以定义其为“递归回路”，即a处结果建立在b处结果基础上，按递推式却发现b处结果又建立在a处结果基础之上。
这种特征的递归是比较容易碰到的，其参数在右侧递归中既有>n的也有<n的，即递归参数不是单调的往一个方向变化。这种情况我们要学会分析、识别【它不能直接使用后面介绍的dp算法，如果能改进成不是回路型的，则可以考虑dp】。

  1. 消除“递归回路”一个例子 例如下图所示：m*n方格中摆放着价值不等的宝贝（价值可正可负），从左上角到达右下角的所有可能路线中，能捡到宝贝的最大值是多少？注：每个格子只能走一遍，并且走到的格子宝贝一定会被捡起。
    假设宝贝价值存放在数组a[M][N]中，用f(i,j)表示从a[i][j]出发到达右下角a[m-1][n-1]能捡到的最大价值和，调用f(0,0)即可，尝试着分析下面<1><2>的关于f(i,j)的递推关系式。
    在这里插入图片描述

<1>如果只能从当前格子向右或向下走到相邻格。 //这种情况不存在“递归回路”，因为只要走出去了，永远都不会走回去。
<2>如果只能从当前格子向上、向下或向右走到相邻格。（选做）
//这种情况存在“递归回路”，但可以想办法增加递归个数来消除递归回路，有兴趣可以思考尝试,也可以文件夹中“百度之星”的一道题目解题思路。
<3>如果从当前格子能向上、向下、向左、向右走到相邻格。 //这种情况存在的“递归回路”无法消除，最终只能采用搜索型算法。

qsort/sort

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

动态规划

在这里插入图片描述
在这里插入图片描述
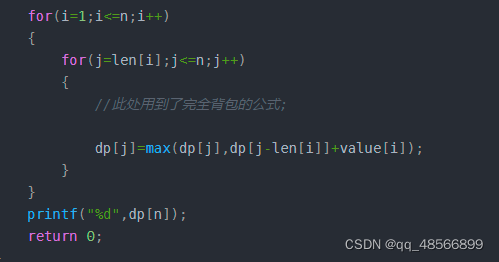
https://blog.csdn.net/qq_43788669/article/details/108985146?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0.no_search_link&spm=1001.2101.3001.4242.1

#include<iostream>
#include<cstdio>
using namespace std;

int main()
{
	int n,i,j,k,len[1005]={0},value[1005]={0},dp[1006]={0};
	scanf("%d %d",&n,&k);
	for(i=1;i<=k;i++)
	{
		scanf("%d",&len[i]);	
	} 
	for(i=1;i<=k;i++)
	{
		scanf("%d",&value[i]);
	}
	
	for(i=1;i<=n;i++)
	{
		for(j=len[i];j<=n;j++)
		{
			//此处用到了完全背包的公式; 
			
			dp[j]=max(dp[j],dp[j-len[i]]+value[i]);
		}
	}
	printf("%d",dp[n]);
	return 0;
}

原文链接：https://blog.csdn.net/qq_43788669/article/details/108985146

在这里插入图片描述
在这里插入图片描述

整数拆分

在这里插入图片描述

求解数字和为sum的方法数问题

long solve(){
	for(int i = 0; i <= n; ++i)
    {
        dp[i][0] = 1;
    }
    
    for(int j = 1; j <= sum; ++j)
    {
        dp[0][j] = 0;
    }
    
    for(int i = 1; i <= n; ++i)
    {
        for(int j = 1; j <= sum; ++j)
        {
            if(a[i] > j)
            {
                dp[i][j] = dp[i-1][j];
            }
            else
            {
                dp[i][j] = dp[i-1][j] + dp[i-1][j-a[i]];
            }
        }
    }
    return dp[n][sum];
}

求解资源分配问题

void Plan()
{
	int maxf, maxj;
	for (int j = 0; j <= n; j++)
		dp[0][j] = 0;

	for (int i = 1; i <= m; i++)
	{
		for (int s = 1; s <= n; s++)
		{
			maxf = 0;
			maxj = 0;
			for (int j = 0; j <= s; j++)
			{
				if ((v[i][j] + dp[i - 1][s - j] >= maxf))
				{
					maxf = v[i][j] + dp[i - 1][s - j];
					maxj = j;
				}
			}
			dp[i][s] = maxf;
			pnum[i][s] = maxj;
		}
	}
}

求解编辑距离问题

void solve()
{
	int i, j;
	for (i = 1; i <= a.length(); i++)
		dp[i][0] = i;
	for (j = 1; j <= b.length(); j++)
		dp[0][j] = j;

	for (i = 1; i <= a.length(); i++)
	{
		for (j = 1; j <= b.length(); j++)
		{
			if (a[i - 1] == b[j - 1])
				dp[i][j] = dp[i - 1][j - 1];
			else
				dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
		}
	}
}

求解会议安排问题

#include <stdio.h>
#include <string.h>
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
#define MAX 101
struct NodeType
{
    int b;                            //开始时间
    int e;                            //结束时间
    int length;                        //订单的执行时间
};
 bool cmp(const NodeType &a,const NodeType &b)
{    //用于排序的运算符重载函数
        return a.e<b.e;                //按结束时间递增排序
}
int n;                            //订单个数
NodeType A[MAX];    //存放订单
int dp[MAX];                    //动态规划数组
int pre[MAX];                    //pre[i]存放前驱订单编号

void solve();
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
      cin>>A[i].b>>A[i].e;
    for (int i=0; i<n; i++)
        A[i].length=A[i].e-A[i].b;
    solve();
    cout<<dp[n-1]; //结果在这个单元中，则递归模型调整成f(n)形式 
    return 0;
}

/* 请在这里填写答案 */
void solve() //从函数参数、返回值形式看，显然只能写成循环型写法 
{//f(i)结果存入dp[i]，按依赖关系，显然从左往右计算 
	sort(A,A+n-1,cmp);//A[0]~A[n-1]按结束时刻递增 排序
	int i,k;
	for(i=0; i<=n-1; i++) //从左往右
	{
		for(k=i-1;k>=0;k--)
		   if(A[k].e <= A[i].b) break; //a[k]是可以安排在A[i].b时刻之前的且序号最大的活动
		if(k<0) dp[i] = max(dp[i-1] , A[i].length); //安排A[i]后，已经没有其它可以安排的活动了 
		else    dp[i] = max(dp[i-1] , A[i].length + dp[k]);		
	}	 
}

兔子繁殖

在这里插入图片描述

int F1[MAX],G1[MAX];//对应f(n),g(n)的存储
int g1(int n)//根据g(n)等价的递推关系式而写
{
	if(n<1)   return 0;//异常
	if(G1[n]) return G1[n];//如果G[n]已经计算过，直接返回结果
	if(n==1)  return G1[n]=1;//保存结果并返回
	else      return G1[n]=g1(n-5)+g1(n-4)+g1(n-3)+g1(n-2);
}

int f1(int n)//求f(n)
{
	int k;
	if(n<1)   return 0;//异常
	if(F1[n]) return F1[n];//如果F[n]已经计算过，直接返回结果
	for(k=n-4;k<=n;k++) 
		F1[n] += g1(k); //对应f(n)=∑g(k) ，n-4<=k<=n
	return F1[n];
}

int G2[MAX]={0};//
int g2(int n)//根据g(n)等价的递推关系式而写
{
	int i;
	if(n<1)   return 0;//异常
	for(i=1;i<=n;i++)
		if(i==1)  G2[i]=1;
	    else      
		{
			for(int j=i-5;j<=i-2;j++)
			  if(j>0) G2[i] +=G2[j];//g[i]=g[i-5]+g[i-4]+g[i-3]+g[i-2]
              //i,j都表示月份，i值可能为2,3,4,5,里面有j<1情况 
		}
	return G2[n]; 
	/* 按g(n)常规写法的代码如下
	for(i=1;i<=n;i++)
		if(i==1)  G2[i]=1;
		else if(i==2) G2[i]=0; 
		else if(i==3) G2[i]=1;
		else if(i==4) G2[i]=1;
		else if(i==5) G2[i]=2;
	    else      
		{//处理i>=6 
		    G2[i]=G2[i-5]+G2[i-4]+G2[i-3]+G2[i-2];
			//for(int j=i-5;j<=i-2;j++) 
			   //if(j>0) G2[i] +=G2[j];//i>=6时，if(j>0)可以省 
		}
	*/
}

int F2[MAX]={0};
int f2(int n)//求f(n)
{
	int i; 
	if(n<1)  return 0;//异常
	for(i=n-4;i<=n;i++) 
		F2[n] += G2[i]; //对应f(n)=∑g(k) ，n-4<=k<=n
      //此处G2[i]也可以改为调用了g2(i)，因为g2算的结果已经放在全局G2[]中，所以可以直接引用已经算好的值 
	return F2[n];
}

//G3[6]为f3,g3共享，存放近6个月新生兔子对数
int G3[6];//压缩存储写法：只用存储g(n-5)~g(n)这6个值
int f3(int n)
{
	int i,s=0;
	if(n<1)  return 0;//异常
	if(n>5)  n=5; //如果n>5，直接将G3[0]~G3[4]累加返回即可
	for(i=0;i<n;i++) 
		s += G3[i]; //对应f(n)=∑g(k) ，n-4<=k<=n
	return s;
}
int g3(int n)
{
	int i,j;
	memset(G3,0,6*sizeof(int));
	G3[0]=1;
	G3[1]=0;
	G3[2]=1;
	G3[3]=1;
	G3[4]=2; //初始化前5个月新生兔子数，类似于斐波那契数列初始时f1=1;f2=1;
	for(i=6;i<=n;i++)//求第i个月新生兔子数，存放在G3[5]中
	{
		G3[5]=G3[0]+G3[1]+G3[2]+G3[3];
		for(j=0;j<5;j++) G3[j]=G3[j+1];//覆盖已经无用的G3[0],即第i个月~第i-4个月的新生兔子数依次存放在G3[4]~G3[0]中
	}
	//当for结束后，则第n个月~第n-4个月的新生兔子数依次存放在G3[4]~G3[0]中
	if(n<5) return G3[n-1];
	else    return G3[4];
}

杨辉三角

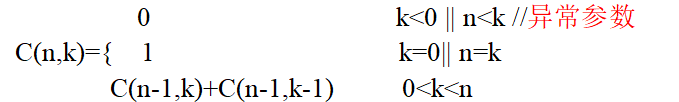
在这里插入图片描述
递归型写法


int a[N][N]; //均初始化为0了
int f1(int n,int k)  
{
   If(k<0 || n<k)  return 0; //异常语句在最前面
   If(a[n][k])     return a[n][k]; //该语句不能在最前面的原因？
If(k==0 || k==n) return a[n][k]=1;
   else          return a[n][k]=f1(n-1,k)+f1(n-1,k-1);//注意这里是递归调用
}

可以在输入n后对n做出限制
if(n>=50) return 1; // n太大时组合数会超出int范围

非递归写法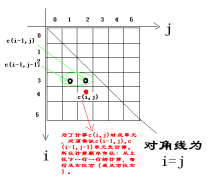在这里插入图片描述

二维数组中，只用到了主对角线的下半部分，所以函数为

Int f2(int n,int k)
{
   Int I,j,b[N][N]={0}; //与f1函数的存储分开，互不干扰
   for(i=0;i<=n;i++)
     for(j=0;j<=i;j++)
       if(j==0 || j==i) b[i][j]=1;
       else         b[i][j]= b[i-1][j]+b[i-1][j-1]; 
   return b[n][k];
}

写法三：//压缩存储写法，结果在b1[],b2[]数组中

//压缩版本1
Int f3(int n,int k)
{
   Int I,j,b1[N],b2[N]; //与f1,f2函数的存储分开，互不干扰
   Int *p1=b1, *p2=b2,  *p; //p1是上一行，p2是下一行
   for(i=0;i<=n;i++)
   {
     for(j=0;j<=i;j++)
     { 
       if(j==0 || j==i) p2[j]=1;
       else         p2[j]=p1[j]+p1[j-1]; 
      }
     p=p1; p1=p2; p2=p; //两个指针交换
   }
   return p1[k]; //for结束后，p1是最后一行
}

//压缩版本2 
Int f3(int n,int k)
{
   Int I,j,b1[N],b2[N]; //与f1,f2函数的存储分开，互不干扰  
   for(i=0;i<=n;i=i+2)//一次算2行
   {
     for(j=0;j<=i;j++)//先算奇数行b1[ ]
     { 
       if(j==0 || j==i) b1[j]=1;
       else         b1[j]=b2[j]+b2[j-1]; 
     }
     for(j=0;j<=i+1;j++)//后算偶数行b2[ ]
     { 
       if(j==0 || j==i) b2[j]=1;
       else         b2[j]=b1[j]+b1[j-1]; 
     }
   }
   If(n%2) return b2[k]; //b2[]存储了n=1,3,5,7…行的组合数
else   return b1[k]; //b1[]存储了n=0,2,4,6…行的组合数
}

//压缩版本3 
Int f3(int n,int k) //压缩成一个数组
{
   Int i,j,a[N]; //
   for(i=0;i<=n;i++)//循环体中计算C(i,j)
   {
     for(j=i;j>=0;j--)//
     { 
       if(j==0 || j==i) a[j]=1;
       else         a[j]=a[j]+a[j-1]; 
     }
   }   
return a[k]; //a[k]即为C(n,k)
}

一副扑克牌（两张鬼牌除外）任取k张牌，不计花色

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

整数2019分解成不同质数之和，有多少种方法

在这里插入图片描述

回溯、分枝限界

在这里插入图片描述

在这里插入图片描述

1~n的全排列

int  X[100],used[100],n, cnt=0; //键盘输入的n小于100
int  xianjie(int k, int i)//判断X[k]能否取i
{
   if(used[i] >0)  return 0; //used[i]>0时表示数字i已经被使用过
   //if(cnt>=20)  return 0; //此剪枝可选用：只输出前20个排列结果
   return 1;
}
void  f(int k)
{  int  i;
   if(k-1==n)  { 输出++cnt:    输出X[1]~X[n]; }
   else for(i=1;i<=n;i++)
       if(xianjie(k,i))
       {   
X[k]=i;
used[i]++; //数字i已经被使用的次数+1，从而在递归f(k+1)里面used[i]都是增加1之后的值
         f(k+1); //遍历  x[k]取i  处的一颗子树
         used[i]--;//f(k+1)结束后，准备遍历旁边一棵子树（即x[k]取i+1 处的子树），x[1]~x[k-1]没有变化，
//仅X[k]换成 i+1了，所以在旁边这棵子树中数字i的使用次数应-1
}
}
void main(void)
{
   cout<<"Enter n:";
   cin>>n;
   f(1);
}

n皇后的结果

int  X[100],n; //键盘输入的n小于100
int  a[100],b[200],c[200];  //初始值均为0
//b[]记录所有45度对角线上是否有皇后，c[]记录135度方向
int  xianjie(int k, int i)//判断X[k]能否取i，即第k行皇后能否摆在i列
{  int  j;   
if(a[i]        //i列已经有皇后了
|| b[k+i-1]    //(k,i)位置45度方向已经有皇后了
|| c[k-i+n])   //(k,i)位置135度方向已经有皇后了
return 0; 
   return 1;
}
void  f(int k)
{  int  i;
   if(k-1==n)  输出X[1]~X[n];//也可以改进成输出二维矩阵
   else for(i=1;i<=n;i++)
       if(xianjie(k,i)) //检验k行皇后能否摆在i列
       {   
X[k]=i; 
a[i]=1;  b[k+i-1]=1;  c[k-i+n]=1;
         f(k+1); 
a[i]=0;  b[k+i-1]=0;  c[k-i+n]=0; //状态量还原
}
}
void main(void)
{
   cout<<"Enter n:";
   cin>>n;
   f(1);
}

输出由数字0,1,3,4,6,7,9构成的所有能够被9整除、数字允许重复、十位数>=个位数的、 m位奇数（1<m<100，由键盘输入）、而且9的出现次数不少于m/3。

int  X[100],m; //键盘输入的m小于100
int  a[]={0,1,3,4,6,7,9};  
int  xianjie(int k, int i)//判断X[k]能否取a[i]
{  int  j,sum=0,count9=0;   
	if(k==1 &&a[i]==0)  return 0;  //最高位数字X[1]不能等于0
	if(k==m) //判断个位数字能否等于a[i]
	{
   		if(X[m-1]<a[i])   return 0; //十位数比个位数小，不允许
   		if(a[i]%2==0)    return 0; //a[i]不是奇数
   		if((sum+a[i])%9)  return 0; //该数不能被9整除
	}
	if(a[i]!=9)
{
  	 	if(count9+ ( m-k) < m/3)  return 0; //9的次数不可能达到m/3个
}
   	return 1;
}
void  f(int k)
{  int  i;
   if(k-1==m)  输出X[1]~X[m]; 
   else for(i=0;i<=6;i++)
       if(xianjie(k,i)) //检验数字X[k]能否取用a[i]
       { 
		X[k]=a[i];  
		sum=sum+a[i];
		if(a[i]==9) count9++;
        f(k+1); 
		sum=sum-a[i];   //递归调用结束后，状态量对称还原
		if(a[i]==9) count9--;
		}
}
void main(void)
{
   cout<<"Enter m:";
   cin>>m;
   f(1);
}

子集的元素之和为S

在这里插入图片描述

int  a[100]= {0,9,7,5,3,2,1}; //本程序中不用a[0]，解其它集合时可以补写初始化函数
int  X[100] , n=6,S=15; 
int  sumS=0, leftS=27; //leftS初值为集合元素之和。
int xianjie(int  k,  int  t)//判断X[k]能否取t，即集合元素a[k]能否划分到子集t
{  
   if(t==1 &&  sumS+a[k]>S)  return 0;//如果a[k]划分到子集1导致其和大于S
   //上面语句是X[k]取1的约束逻辑，下面代码是X[k]取0的约束逻辑
   if(t==0 && sumS+leftS-a[k]<S)  return 0;//在X[k]待定时leftS中包含了a[k]
   return  1;
}
void  f(int k)
{  	int  i;
	if(k-1==n) //到叶子节点的标志
	{	if(sumS==S) //如果子集1的元素和为S，则输出该子集
		{
			cout<<endl<<"{";
			for(i=1;i<=n;i++)
				if(X[i]==1) cout<<a[i]<<", ";
				cout<<"}";
		}
	}
	else for(i=0;i<=1;i++)
     if(xianjie(k,i))
	 { 	X[k]=i;
        if(i==1) sumS=sumS + a[k];
        leftS =leftS - a[k];
		f(k+1); 
        if(i==1) sumS=sumS - a[k]; //共享状态量必须还原
        leftS =leftS + a[k];
	 }
}
void main(void)
{
	f(1);
}

1-n表达式

#include<stdio.h>
char a[]=" +-*/";
int x[100],n=9,cnt=0,used[100];//used[0]~used[4]记录运算符次数 

/*在1~n(=9)的数字之间任意加入加、减、乘、除或不加，
输出所有可能的表达式
还可以增加约束：
  至少3个加，至少3个乘，不能用除，乘不能连续出现3个 
  
  分析.本质就是从0~4任取8个（允许重复取）进行全排列 
  所以回溯函数的框架如f(k)函数，上面4个约束由
  jianzhi(k,i)函数控制实现。 
  
*/ 

void output()
{
	int i;
	printf("\n%d:",++cnt);
	for(i=1;i<n;i++) 
	   printf("%d%c",i,a[x[i]]);
	printf("%d",n);
}

int jianzhi(int k,int i)
{
	int j;
	
	//不允许连续出现3个乘 
	if(i==3 && k>2 && x[k-1]==3 && x[k-2]==3)
	    return 0;
	//至少3个加
	if(i!=1 && used[1]+8-k<3) return 0;
	//至少3个乘 
	if(i!=3 && used[3]+8-k<3) return 0;
	//隐含剪枝逻辑:加与乘 出现次数和 >= 6 
	if(i!=1 && i!=3 && used[1]+used[3]+8-k<6)
	                    return 0; 
	//不能用除 
	if(i==4) return 0;
	return 1; 
} 

void f(int k)//x[1]~x[k-1] 
{
	if(k>8) output();
	else for(int i=0;i<=4;i++)
	   if(jianzhi(k,i)) 
	   {
		  x[k]=i;
		  used[i]++; 
		  f(k+1);
		  used[i]--;
	   }
}

int main()
{
	//scanf("%d",&n);
	f(1);
	return 0;
}

分枝限界

在这里插入图片描述
在这里插入图片描述

迷宫

回溯

#include<iostream>
using namespace std;
int mg[9][9]=
{
 {1,1,1,1,1,1,1,1,1},
 {1,0,0,1,0,0,1,0,1},
 {1,0,0,1,1,0,0,0,1},
 {1,0,1,0,1,1,0,1,1},
 {1,0,0,0,0,1,0,0,1},
 {1,1,0,1,0,1,0,0,1},
 {1,1,0,1,0,1,0,0,1},
 {1,1,0,1,0,0,0,0,1},
 {1,1,1,1,1,1,1,1,1}
};
int n,a,b,c,d,Min,step;
int offset[4][2]={{1,0},{-1,0},{0,1},{0,-1}};

int jianzhi(int x,int y,int i)
{
	int x1=x+offset[i][0],y1= y+offset[i][1];
	if(x1<0 || x1>8 || y1<0 || y1>8) return 0;
	if(mg[x1][y1]) return 0;
	if(step>Min)  return 0;
	return 1;
}

void f(int x,int y)
{//回溯最大的缺点，运算量难以控制 
	if(x==c && y==d)
	{
	   if(step-1<Min) Min=step-1;		
	}
	else for(int i=0;i<4;i++)
	  if(jianzhi(x,y,i))
	  {	 int x1=x+offset[i][0],y1= y+offset[i][1];	 
	  	 mg[x1][y1] = step;
	  	 step++;
	  	 f(x1,y1);
	  	 mg[x1][y1] = 0;
	  	 step--;
	  }
}

int main()
{
	cin>>n;
	while(n--)
	{
		cin>>a>>b>>c>>d;
		Min=100;
		step=1;
		f(a,b);	
		cout<<Min<<endl;	
	}
	return 0;
}

广搜

#include<iostream>
#include<memory.h>
#include<queue>
using namespace std;
int mg[9][9]=
{
 {1,1,1,1,1,1,1,1,1},
 {1,0,0,1,0,0,1,0,1},
 {1,0,0,1,1,0,0,0,1},
 {1,0,1,0,1,1,0,1,1},
 {1,0,0,0,0,1,0,0,1},
 {1,1,0,1,0,1,0,0,1},
 {1,1,0,1,0,1,0,0,1},
 {1,1,0,1,0,0,0,0,1},
 {1,1,1,1,1,1,1,1,1}
};
int n,a,b,c,d,m[9][9];
int offset[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
struct node{ int x,y,step;};//起点到(x,y)，已经走了step步骤 

int jianzhi(node e,int i)
{	int x1,y1;
	x1 = e.x+offset[i][0];
	y1 = e.y+offset[i][1];	
	if(x1<0 || x1>8 || y1<0 || y1>8) return 0;
	if(m[x1][y1] || mg[x1][y1])      return 0;//(x1,y1)为已跳过、障碍物，m[][]，mg[][]
	return 1;
}

int main()
{   
    int i;
    node e,e1;
	cin>>n;
	queue<node>Q;	
	while(n--)
	{
		cin>>a>>b>>c>>d;
		e.x = a; e.y = b; e.step = 0; //根节点
		m[a][b]=1;
		Q.push(e); 
		memset(m,0,sizeof(m));
		while(!Q.empty())
		{	
		   e=Q.front();
		   Q.pop();
		   if(e.x==c && e.y==d) break;
		   for(i=0;i<4;i++)	
		      if(jianzhi(e,i)) 
			  {
			  	e1.x = e.x + offset[i][0];
			  	e1.y = e.y + offset[i][1];
			  	e1.step = e.step +1;
				m[e1.x][e1.y]=1;
			  	Q.push(e1);
			  }
		}
		if(e.x ==c && e.y ==d) cout<<e.step<<endl ;
		else  cout<<"无法到达"<<endl;
		while(!Q.empty())	Q.pop();
	}
	return 0;
}

A星

#include<iostream>
#include<memory.h>
#include<queue>
#include<algorithm>
using namespace std;
int mg[9][9]=
{
 {1,1,1,1,1,1,1,1,1},
 {1,0,0,1,0,0,1,0,1},
 {1,0,0,1,1,0,0,0,1},
 {1,0,1,0,1,1,0,1,1},
 {1,0,0,0,0,1,0,0,1},
 {1,1,0,1,0,1,0,0,1},
 {1,1,0,1,0,1,0,0,1},
 {1,1,0,1,0,0,0,0,1},
 {1,1,1,1,1,1,1,1,1}
};
int n,a,b,c,d,m[9][9];
int offset[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
struct node{ 
	int x,y,step,len;
	bool operator < (const node &a) const
	{
		return step+len > a.step+a.len; //小的优先排队头
	}
};
//起点(a,b)到(x,y)，已经走了step步骤,到(c,d)至少还要走len步

int jianzhi(node e,int i)
{	int x1,y1;
	x1 = e.x+offset[i][0];
	y1 = e.y+offset[i][1];	
	if(x1<0 || x1>8 || y1<0 || y1>8) return 0;
	if(m[x1][y1] || mg[x1][y1])      return 0;//(x1,y1)为已跳过、障碍物，m[][]，mg[][]
	return 1;
}

int main()
{   
    int i;
    node e,e1;
	cin>>n;
	priority_queue<node>Q;	
	while(n--)
	{
		cin>>a>>b>>c>>d;
		e.x = a; e.y = b; e.step = 0; e.len = abs(a-c)+abs(b-d);//根节点
		m[a][b]=1;//(a,b)点已经进入队列 
		Q.push(e); 
		memset(m,0,sizeof(m));
		while(!Q.empty())
		{	
		   e=Q.top();
		   Q.pop();
		   if(e.x==c && e.y==d) break;
		   for(i=0;i<4;i++)	
		      if(jianzhi(e,i)) 
			  {
			  	e1.x = e.x + offset[i][0];
			  	e1.y = e.y + offset[i][1];
			  	e1.step = e.step +1;
				e1.len  = abs(e1.x-c)+abs(e1.y-d);//评估代价
				m[e1.x][e1.y]=1;//已经进入队列标志
			  	Q.push(e1);
			  }
		}
		if(e.x ==c && e.y ==d) cout<<e.step<<endl ;
		else  cout<<"无法到达"<<endl;
		while(!Q.empty())	Q.pop();
	}
	return 0;
}
PMP第7章：成本基准易错习题和知识点汇总
zhengzaifeidelushang的博客
06-11 1031
PMP第7章：成本基准易错习题和知识点汇总 1.成本基准是下列哪个过程的输出？ A:规划成本管理 B:估算成本 C:制定预算正确答案 D:控制成本 答案解析： 成本基准是“制定预算“过程的输出。”正确答案：C 以下哪项是估算成本过程的输入？ A:工作分解结构 B:成本基准 C:合同 D:资源日历 答案解析： “工作分解结构属于范围基准，指明了项目全部可交付成果及其各组成部分之间的相互关系“，是估算成本过程的输入。正确答案：A 3.通过项目状态报告，项目挣值（EV）为0.6，计划价值（PV）为0.1，通过
考研408数据结构第一章线性表核心知识点与易错点详解（附真题示例与避坑指南）
weixin_73064319的博客
03-01 1073
画图辅助分析：对链表操作，务必先画出指针变化示意图。边界检查：对空表、头节点、尾节点等特殊情况优先处理。复杂度优化：若题目要求时间或空间优化，优先考虑双指针、哈希表等技巧。代码鲁棒性：所有操作前检查指针是否为空，避免运行时崩溃。通过系统梳理线性表的核心知识点与易错陷阱，结合真题实战分析，考生可精准把握命题规律，在408考试中避免低级失误，实现高分突破。建议将本文中的代码片段与真题结合练习，强化手写代码能力。
算法设计与分析课件与知识点复习
04-24
课程主要讨论和介绍计算机算法的复杂性理论，结合对一些熟悉的算法进行分析和总结，强化基础理论知识，对一些大型工程软件的分析，会有一定的辅助作用。它主要介绍计算机科学及应用领域常见的有代表性的非数值算法及算法设计的若干重要方法，同时，介绍算法分析的基本知识。阐述计算模型和时间复杂性的定义；讨论递归技术和算法分析的基本手段；介绍算法设计的几类方法，如分治法、回溯法、贪心法、动态规划法、分枝限界法等，并结合某些有实用意义的经典算法来加深设计方法的探讨，由浅入深地进行算法效率分析，使学生在掌握各种算法设计方法和分析基本技术的同时，也是逻辑思维得到锻炼。
汉诺塔
m0_52262443的博客
02-02 223
汉诺塔Ⅴ Problem Description 用1,2,…,n表示n个盘子，称为1号盘，2号盘,…。号数大盘子就大。经典的汉诺塔问题经常作为一个递归的经典例题存在。可能有人并不知道汉诺塔问题的典故。汉诺塔来源于印度传说的一个故事，上帝创造世界时作了三根金刚石柱子，在一根柱子上从下往上按大小顺序摞着64片黄金圆盘。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一回只能移动一个圆盘。我们知道最少需要移动2^64-1次.在移动过程中发现，有的圆
算法设计可练习题One
阿也的博客
09-27 404
算法题目
算法设计练习1 Triangle DP动态规划
weixin_37977536的博客
09-19 329
题目来自leetcode上的Array类的习题，题目如下。 题目链接：https://leetcode.com/problems/triangle/description/ 这是一道难度中等的题目，leetcode上的通过率为36%。 题目要求我们寻找从三角形的顶端到底部的最短路径，即pick到的数之和最小。题目规定每次只能移动到adjacent numbers on the row b...
算法设计习题(1-6)
weixin_43869415的博客
07-12 1708
文章目录前言一、第一章1.1 带解答的练习1.1.1 练习11.1.2 练习2![在这里插入图片描述](https://img-blog.csdnimg.cn/20210711151855832.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80Mzg2OTQxNQ==,size_16,color_FFFFFF,t_70)1.2 课
软件设计师真题+个人对比真题总结的知识点.rar
04-12
通过对历年真题的深度练习和对知识点的总结，考生可以更好地理解和掌握软件设计的精髓，提高备考效率，提升通过考试的可能性。同时，这个过程也能帮助实际工作中提升软件设计和问题解决的能力。
软考中级软件设计师-历年真题+知识点+重点笔记（完整版）
11-09
《软考中级软件设计师：历年真题解析与重点知识点详解》 软考中级软件设计师是一项针对计算机技术应用和设计能力的认证考试，旨在评估并提升考生在软件开发、设计及项目管理等方面的综合技能。这份资源集合了历年来...
蓝桥杯Python竞赛试题解析：涵盖基础语法、逻辑推理与算法设计
最新发布
03-03
使用场景及目标：①帮助参赛者熟悉历年考试题目的难度分布及重点知识点覆盖；②通过典型实例训练编程思维与技巧；③鼓励使用者深入研究Python特性并将其应用于解决问题的过程之中；④促进对复杂算法的理解与掌握，...
Algorithm Design算法设计习题答案（1）
11-10
Algorithm Design算法设计习题答案（1） 1-6章 内有密码
会议安排（贪心算法和动态规划） 贪心算法和动态规划.pdf
04-08
会议安排（贪心算法和动态规划） 贪心算法和动态规划.pdf
C++算法设计分析会场安排问题
05-17
算法设计与分析课后程序实现会场安排。 // 会场安排问题 // #include<iostream> #include <algorithm> #include<fstream> using namespace std; int greedy(int n,int *a,int *b) //贪心选择 { int sum=0,curr=0,i,j,k; int *x; x=new int[2*n]; for(i=j=0;i<n;i++,j+=2) { x[j]=a[i]; x[j+1]=b[i]; } sort(a,a+n); //排序
算法程序与设计知识点总结
nanaz11的博客
12-23 1049
算法是指解决问题的方法或者过程，是满足下列性质的指令序列：（1）输入：有0个或多个外部量作为算法的输入（2）输出：算法产生至少一个量作为输出（3）确定性：组成算法的每条指令是清晰的，无歧义的（4）有限性：算法中每条指令的执行次数有限，执行每条指令的时间也有限。程序是算法用某种程序设计语言的具体实现。程序可以不满足算法的性质四 可操作性最好且有实际价值的是最坏情况下的时间复杂性，O复杂度上界，Ω下...
数据结构练习题二算法设计（2、3、5、8）
m0_52180541的博客
10-25 162
SqList.h #include<stdio.h> #include<stdlib.h> #define MaxSize 100 typedef int ElemType; //---------------------------------2、3----------------------- typedef struct { ElemType data[MaxSize]; int length; }SqList; void InitList(SqList &
《算法分析与设计》练习3
qq_52348590的博客
07-04 925
目录 A 超级青蛙 B 汉诺塔 C 汉诺塔2 D kimi的早餐店 E 字母全排列 F 九数组分数 A 超级青蛙 题目描述 一只超级青蛙一次可以跳上1级台阶，也可以跳上2级……它也能够跳上n级台阶。请问，该青蛙跳上一个n级的台阶总共有多少种跳法？ 输入 输入一个正整数n表示台阶的数量。 输出 输出总的跳法数。 样例输入Copy 1 2 样例输出Copy 1 2 分析：一般来说，要用递归，肯定是有递归表达式的，嘿嘿嘿 当然递归表达式就...
作业比赛编号 : 1271 - 2022年春季学期《算法分析与设计》练习9
weixin_51250562的博客
06-01 457
最大子段和 题目描述 给定n个整数（可能是负数）组成的序列a[1], a[2], a[3], …, a[n]，求该序列的子段和如a[i]+a[i+1]+…+a[j]的最大值。 输入 每组输入包括两行，第一行为序列长度n，第二行为序列。 输出 输出字段和的最大值。 样例输入Copy 5 -1 0 1 2 3 样例输出Copy 6 #include<cstdio> #include<iostream> #include<alg...
第八章 高效算法设计相关知识点总结
好好学习，天天向上
10-10 628
第八章 高效算法设计相关知识点总结
算法知识点整理
woshibendangao的专栏
08-06 1834
1、算法的几个基本特征是什么？
蓝桥杯Python试题详解：提升基础到算法设计能力
资源摘要信息:"本文详细解析了蓝桥杯Python竞赛的试题，旨在帮助参赛者熟悉比赛的难度分布及重点知识点，并通过典型实例训练编程思维与技巧。本文涵盖的内容包括基础知识、基本语法概念检查、编程练习题，以及一些...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值