算法分析：分治法。

最新推荐文章于 2022-06-17 18:37:16 发布

ai其实很简单

最新推荐文章于 2022-06-17 18:37:16 发布

阅读量524

点赞数 12

文章标签：算法数据结构 c++

本文链接：https://blog.csdn.net/qq_48574847/article/details/124782630

版权

算法设计：分治法

在显示中，分而治之往往是将大片区域分成小块区域治理，算法中往往用递归来解决分治问题。

1.## 分治算法的设计思想
对于一个规模为n的问题，当问题可以很容易直接解决，则可以直接解决该问题。但当难以解决该问题时，可以将该问题分解为k个规模较小的子问题，这些子问题之间相互独立且与原问题形式相同，递归的解决这些子问题，最终将子问题合并得到原问题的解。
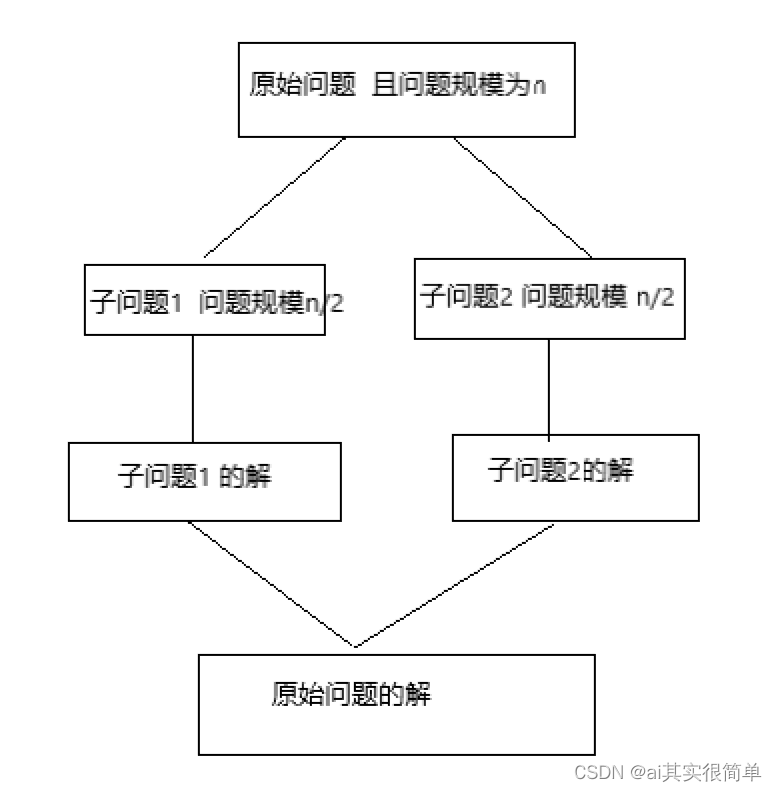
请添加图片描述

2.分治法的解题步骤

分解：将要解决的大问题分解成若干个规模更小的子问题，且这些子问题相互之间独立，与原问题形式相同。
治理：由于子问题与原问题形式相同，所以可以继续分解各子问题，当子问题规模足够小时，就可用简单的方法进行求解。
合并：将子问题的解合并成原问题的解。

简单来说，分治法就是将一个难以解决的大问题，分割程一些形式相同的小问题，将这些小问题各各求解，分而治之。

总的来说分治法的设计模式：

返回值 divide_and_conquer(p){
	if(p<=n0){	//当规模小于n0时 
		return 结果; 
	}
	//将p分解成规模更小的子问题p1，p2.。。 
	for(int i=0;i<k;i++){
		yi=divide_and_conquer(pi);	//递归解决各各子问题 
	} 
	return merge(y1,y2....);
}

3.在数据结构中分治法的应用

先序遍历二叉树
先序遍历二叉树的操作：当二叉树为空时，反回空；否则 1）先访问根节点 2）访问左子树 3）访问右子树。此时不难看出可将原问题（先序遍历二叉树）可以分解成两个子问题，一个是先序遍历左二叉树，另一个是先序遍历右二叉树。子问题还可继续分解，当访问到根节点时可将子问题求解并返回给原问题。

递归的写法：

void PreOrder(){
	if(T!=NULL){
		visit(T);	//访问根节点 
		PreOrder(T->lchild);	//分治遍历左子树 
		PreOrder(T->rchild);	//分治遍历右子树 
	}
}`

非递归形式：

void PreOrder(BiTree T){
	InitStack(S);	//初始化一个栈 
	BiTree p=T;		//p为指针 
	while(p||!IsEmpty(S)){	//栈不为空或p指针存在时 
		if(p){
			Push(S,p);	//入栈
			visit(p);
			p=p->lchild; 
		} else{
			Pop(S,p);	//出栈 
			p=p->rchild;
		}
	} 
}

中序遍历类似，不再进行讲解。

后续遍历二叉树
递归形式与先序遍历类似。

非递归形式：与非递归先序遍历二叉树类似，后序非递归遍历二叉树是先访问左子树，再访问右子树，最后再访问根节点。设置栈来进行存储节点，但必须区分返回根节点（子问题的答案）时，是从左子树返回的，还是右子树返回的。所以此时应该使用一个辅助指针r，用来记录最近访问过的节点，判断节点是否为理论上的叶子节点（左右子树都被访问过）。

PostOrder(BiTree T){
	InitStack(S);
	BiTree p=T;
	BiTree r=NULL;	//设置一个辅助指针，记录最近指向的节点 
	while(p||!IsEmpty(S)){
		if(p){
			Push(S,p);	//入栈
			p=p->lchild; 
		}else{
			GetTop(S,p); //获得栈顶节点
			if(p->rchild&&p->rchild!=r){
				p=p->rchild;
				Push(S,p);
				p=p->lchild;
			} else{
				Pop(S,p);
				visit(p);
				r=p;	//记录最近访问过的节点
				p=NULL;	//重置p节点 
			}
		}
	} 
}

求解树的高度
求解一颗二叉树的树高时，可将原问题（二叉树的树高）分解成两个子问题（求解左右子树的树高），再将子问题进行分解，，当分解到只有一个根节点时返回1，从而返回子问题的解给原问题，求出原问题的解。

递归形式：

int Btdepth(BiTree T){
	if(T==0){	//当树为空时 
		return 0;
	}
	int ldepth=Btdepth(T->lchild);//记录左子树的树高 
	int rdepth=Btdepth(T->rchild);//记录右子树的树高 

	return fmax(ldepth,rdepth)+1; //返回左右子树高度最大值+1 
}

非递归形式：
采用层次遍历算法思想，设置level记录当前节点所在的层数，设置last指向当前节点的最右节点。每次出队时都与last进行比较，若相等则层数+1，并让last指向下一层的最右节点。

int Btdepth(BiTree T){
	if(T==0)	return 0;//当树为空时
	int front=-1,rear=-1;//两个指针分别指向队头和队尾
	int level=0,last=0;//level：记录层数 last：指向该层的最后一个节点
	BiTree p;
	BiTree Q[MaxSize];
	Q[++rear]=T;	//根节点入队 
	while(front<rear){
		p=Q[++front];	//出队
		if(p->lchild!=NULL){
			Q[++rear]=p->lchild;
		} 
		if(p->rchild!=NULL){
			Q[++rear]=p->rchild;
		}
		if(front==last){
			level++;
			last=rear;	//last指向下一层 
		}
	}
	return level; 		
}

根据二叉树的先序遍历和中序遍历求出二叉树
二叉树的先序遍历的形式为：根、左子树、右子树
二叉树的中序遍历的形式为：左子树、根、右子树
所以可知先序遍历时第一个节点为该树的根节点，从中序遍历中找到该节点的位置则可以找出左右子树的节点分别为多少。此时根据分治法的思想再将原问题分解成子问题，即求解左右子树的子问题，最终将子问题求解的答案返回给原问题。

BiTree PreInCreat(ElemType A[],ElemType B[],int l1,int h1,int l2,int h2){
	//A数组保存先序序列 B数组保存中序序列 		数组全从1开始记录 
	//l1：先序序列的第一个位置的下标  h1：先序序列的最后一个位置的下标 
	//l2：中序序列的第一个位置的下标   h2：中序序列的最后一个位置的下标 
	int i;//记录根节点在中序序列中的位置 
	BiTree root = (BiTree)malloc(sizeof(BiTNode));	//给根节点开辟空间
	root->data=A[l1];
	for(i=l2;B[i]!=A[l1];i++);	 //找出根节点在中序序列的位置
	int llen = i-l2;	//左子树的长度
	int rlen = h2-i;	//右子树的长度
	if(llen){	//当左子树不为空时 
		root->lchild=PreInCreat(A,B,l1+1,l1+llen,l2,l2+llen-1);
	}else{
		root->lchild=NULL;
	}
	if(rlen){	//当右子树不为空时 
		root->rchild=PreInCreat(A,B,h1-rlen+1,h1,h2-rlen+1,h2);
	}else{
		root->rchild=NULL;
	}
	return root; 
}

线索二叉树
线索二叉树的复习：基本概念：遍历二叉树其实是按照某一种排列规则将二叉树中的节点进行了线性排列，其中每一个节点（除第一个和最后一个节点）都有一个直接前驱和直接后继。当节点有指针直接指向前驱和后继时称为线索二叉树。实质为将空闲的指针利用起来去保存二叉树的某种遍历的前驱或后继。其中，指向前驱和后继的指针为线索。 （线索二叉树是一种物理结构）

为了实现该操作对每个节点进行改变：加入左右索引标志（ltag、rtag）。

typedef struct ThreadNode{
	ElemType data;//数据 
	struct ThreadNode *lchild,*rchild;//左右孩子指针 
	int ltag,rtag;//索引 
}ThreadNode,*ThreadTree;

ltag:当ltag=0时代表lchild指针指向该节点的左孩子；当ltag=1时代表lchild指针指向的是某种遍历的前驱节点。
rtag：当rtag=0时代表rchild指针指向该节点的右孩子；当rtag=1时代表rchild指针指向的是某种遍历的后继节点。
例如：
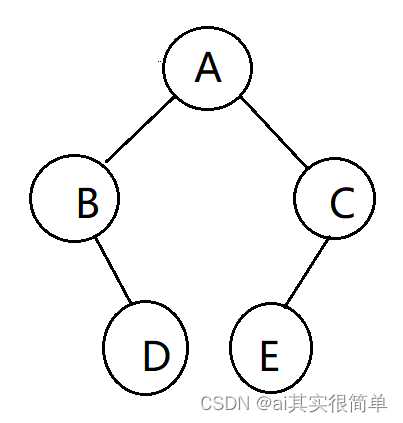
请添加图片描述
该图中中序遍历二叉树为BDAEC，此时B的左指针指向空，且左线索标志为0，则让B的做指针指向前驱即指向NULL，左线索标志等于1；D节点的左右指针都为空，且左右线索标志为0，则让D的左指针指向前驱B，右指针指向后继A，左右线索标志全等于1.。。以此类推。

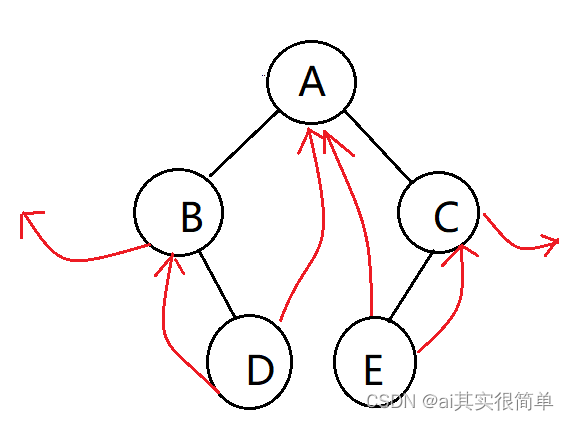
线索二叉树

建立中序线索二叉树的算法思想：建立一个pre指针指向p节点的前驱，检查p指针的左指针是否为空，如果为空则指向pre；再检查pre的右指针是否指向空，如果指向空则指向后继p节点。
代码：

void InThread(ThreadTree &p,ThreadTree &pre){
	if(p!=NULL){
		InThread(p->lchild,pre);//利用分治法递归，线索化左子树 
		if(p->lchild==NULL){
			p->lchild=pre;
			p->ltag=1;
		}
		if(pre->rchild==NULL&&pre!=NULL){
			pre->rchild=p;
			pre->ltag=1;
		}
		pre=p;
		InThread(p->rchild,pre);//利用分治法递归，线索化右子树 
	}
}
void CreateInThread(ThreadTree T){
	ThreadTree pre=NULL;
	if(T!=NULL){
		InThread(T,pre);
		pre->rchild=NULL;
		pre->rtag=1;
	}
}

二分法查找
**注：**二分法查找只适用于有序的顺序表。
算法思想：将关键字key与顺序表中的中间位置进行比较，若相等时：返回答案。若不相等时：将关键字key与顺序表的中间位置进行比较，当key大于中间位置时在顺序表的前半部分进行比较，否则相反。
代码：

int Binary_Search(SeqList L,ElemType key){
	int low=0,high=L.TableLen-1,mid;
	while(low<=high){
		mid=(low+high)/2;
		if(L.elem[mid]==key){
			return mid;
		}else if(L.elem[mid]>key){
			high=mid-1;
		}else{
			low=mid+1;
		}
	}
	return -1; //没有找到 
}

快速排序算法
快速排序是一种基于分治法的一种排序方法，从数据中随机选取一个数（通常是第一个数字），以这个支点为界，将序列划分为两个部分，左边比这个数大，右边比这个数小，然后分别对左右两个部分分别进行递归处理，直至排列好。
策略：
1）设置两个指针i，j。开始时分别指向数据的头和尾，并且在任意时刻都保证i<=j。
2）当支点在i处时：若i[i]<=i[j]，则二者位置合适，j–；否则二者位置不合适，r[i]与r[j]对换，i++。
3）当支点在j处时：若i[i]<=i[j]，则二者位置合适,i++；否则二者位置不合适，r[i]与r[j]对换，j–;
4）递归的重复该操作，直至i与j相等。

代码：

void QuickSort(ElemType A[],int low,int high){
	if(low<high){
		int pivotpos=Pertition(A,low,high);//进行划分 
		QuickSort(A,low,pivotpos-1);//对左边进行递归 
		QuickSort(A,pivotpos+1,high);//对右边进行递归 
	}
} 
int Pertition(ElemType A[],int low,int high){
	//划分区间
	ElemType pivot=A[low];//选出第一个元素作为支点	
	while(low<high){//进行划分 
		while(low<high&&A[high]>=pivot)  --high;
		A[low]=A[high];	//将比支点小的放到左边
		while(low<high&&A[low]<=pivot) 	 ++low;
		A[high]=A[low];//将比支点大的元素放在右边 
	}	
	A[low]=pivot;//支点元素存放在最终位置 
	return low;//返回存放支点元素的最终位置 
}

归并排序
简单来说就是将若干个排序好的有序表合并成一个有序表。

代码：

Elemtype *B=(ElemType*)malloc((n+1)*sizeof(ElemType));
void Merge(ElemType A[],int low,int mid,int high){
	//将两个有序的序列合并成一个有序的序列 mid指向第一个序列的最后一个元素 
	for(int k=low;k<=high;k++){
		B[k]=A[k];//将A中的元素复制到B中 
	} 
	for(int i=low,j=mid+1,k=i;i<=mid&&j<=mid&&j<=high;k++){
		//i指向B中第一个序列的第一个元素  j指向B中第二个序列的第二个元素  k指向a的第一个元素 
		if(B[i]<=B[j]){
			A[k]=B[i];
			i++;
		}else{
			A[K]=B[j];
			j++;
		}
	} 
	//将剩余的序列放入A 
	while(i<=mid) A[k++]=B[i++];
	while(j<=mid) A[k++]=B[j++];
} 
void MergeSort(ElemType A[],int low,int high){
	if(low<high){
		int mid=(low+high)/2;//从中间将序列划分为两段 
		MergeSort(A,low,mid);
		MergeSort(A,mid+1,high);
		Merge(A,low,low,high);
	}	
}

4.常见的分治法算法题

猜数游戏
题目： 随机写1-n范围内的数字（假设有序），以最快的速度找出值为x的数字。
策略： 因为数字有序，所以该题是一个典型的二分查找的问题。用一个一维数组进行存储该有序数列，low和high表示查找范围的上界和下界，middle表示查找范围的中间位置。
1）初始化令low=0，指向数组的第一个元素，high=n-1，指向数组的最后一个元素。
2）middle=（low+high）/2，表示查找的中间元素。
3）判断low和high是否成立，若不成立则返回失败。
4）判断x与s[middle]的大小关系。

#include<iostream>
#include<algorithm>
using namespace std;
const int M=1001;//范围的最大值
int Search(int s[],int n,int x){
	//n:数组的长度 x:所要查找的元素
	int low=0,high=n-1,mid;
	while(low<=high){
		mid=(low+high)/2;
		if(s[mid]==x){
			return mid;
		}else if(s[mid]>x){
			high=mid-1;
		}else{
			low=mid+1;
		}
	}
	return -1;
}
int main(){
	int result=0;//记录结果 
	int n;//数列中元素个数
	cin>>n;
	int x,s[M];	//x所要查找的元素 s【】：数组 
	cin>>x;
	for(int i=0;i<n;i++){
		cin>>s[i];
	} 
	sort(s,s+n);//将数组从小到达排列 
	result=Search(s,n,x); 
	if(result==-1){
		cout<<"该数组中没有要查找的元素"<<endl;
	}else{
		cout<<"该数组中要查找的元素在数组中的数组下标为："<<result<<endl; 
	}
}

棋盘覆盖游戏问题
问题描述： 在一个2k×2k 个方格组成的棋盘中，恰有一个方格与其它方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。

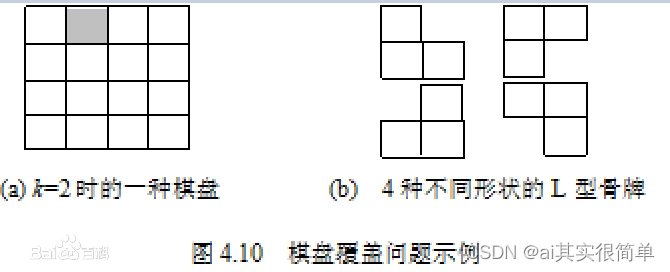
问题分析： 当特殊的方格位于左上角的象限时，在中间位置用一个L型骨牌覆盖其他三个象限。

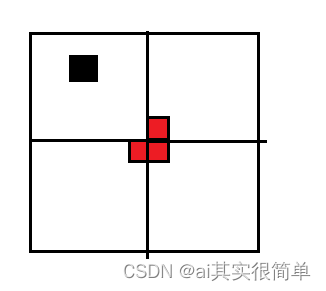
此时，每个象限都可以视为有特殊方格，都需要至少覆盖一个方法，这样可以将原问题分解成为四个子问题，且四个子问题与原问题类似。
特殊方格也可位于左下、右上、右下，解题思想类似。

策略：
1）将棋盘分解成四个相同大小的象限分别为：左上、左下、右上、右下。
2）对每个子棋盘，若有特殊方格再将该棋盘进行同样分解，对每个子棋盘进行递归。若不存在特殊棋盘则用一个L型骨牌与另外两个没有特殊方格的子棋盘进行覆盖成为有特殊方格的棋盘，再进行分解。
3）直到棋盘大小为1*1.

代码：

#include<iostream>
using namespace std;
const board[101][101]={0};
void ChessBoard(int tr,int tc,int dr,int dc,int size){
	if(size==1){	//当棋盘大小为1时，返回 
		return ;
	}
	int t=title++;	//记录L型骨牌号
	int s=size/2;//切分棋盘边长
	//当覆盖左上棋盘时
	if(dr<tr+s&&dc<tc+s){
		ChessBoard(tr,tc,dr,dc,s);//当特殊方格再左上棋盘时	
	}else{
		//当左上棋盘没有特殊方格的时候 用L型骨牌覆盖右下角
		board[tr+s-1][tc+s-1]=t;
		ChessBoard(tr,tc,dr+s-1,dc+s-1,s); 
	} 
	//当覆盖右上棋盘时
	if(dr<tr&&dc>=tc+s){
		ChessBoard(tr,tc+s,dr,dc,s);
	}else{
		//当右棋盘上没有特殊方格时  用L型骨牌覆盖左下角
		board[tr+s-1][tc+s]=t; 
		ChessBoard(tr,tc+s,tr+s-1,tc+s,s);
	}
	//当覆盖左下棋盘时
	if(dr>=tr+s&&dc<tc){
		ChessBoard(tr+s,tc,dr,dc,s);
	}else{
		//当左下棋盘没有特殊方格时  用L型骨牌覆盖右上角
		board[tr+s][tc+s-1]=t;
		ChessBoard(tr+s,tr,tr+s,tr+s-1); 
	} 
	//当覆盖右下棋盘时
	if(dr>=tr+s&&dc>=tc+s){
		ChessBoard(tr+s,tc+s,dr,dc,s);
	}else{
		//当右下棋盘没有特殊方格时  用L型骨牌覆盖左上角
		board[tr+s,tc+s]=t; 
		ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
	}
}

循环日程安排问题
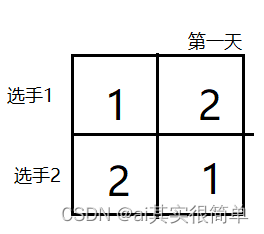
问题描述： 设有n=2^k个选手要进行网球循环赛，要求设计一个满足以下要求的比赛日程表：
①每个选手必须与其他n-1个选手各赛一次；
②每个选手一天只能赛一次。

问题分析： 当有一个参赛选手时（k=1）时

当有四名选手参加比赛（k=2）时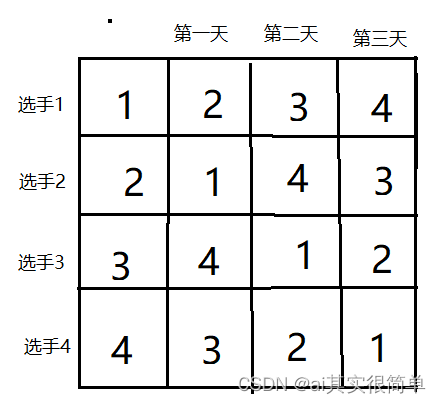
此时不难看出，可以按照要求将比赛日程设计成一个n行n-1列的二维表，其中第i行第j列表示第i个选手再第j天的比赛。其中第一列是认为增加的，取值为1-n的各各选手。

当有八名参赛选手（k＝3）时

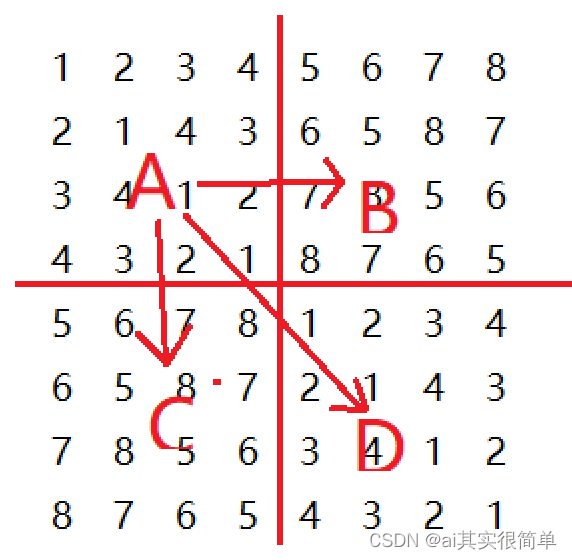
可以将区域划分为4个区域分别为ABCD，观察可知：当A转变为B时，A的每个元素加上A的边长可得B区域的每个元素；当A转变为C时，A的每个元素加上A的边长可得C区域的每个元素；当A转变为D时，每个元素相等。然后再将A区域按同样的策略划分成四个不同的区域进行求解，直至区域大小变成2*2.

算法策略： 建立一个二维数组a存放比赛日程表，从k＝1开始求解，逆向的推出整个比赛日程表。

代码：

int a[MAX][MAX];//存放比赛日程表  其中下标为0的不用
void Plan(int k){
	int n=2;//记录表格大小  从2开始 
	a[1][1]=1;a[1][2]=2;
	a[2][1]=2;a[2][2]=1;
	for(int t=1;t<k;t++){//迭代处理，依次处理2，4，，，2^(k-1)个选手 
		int temp=n;//记录原来子问题的边长 
		n = n*2;//记录返回之后的大问题的方格的边长 
		for(int i=temp+1;i<=n;i++){//填写左下角的元素 i代表行 
			for(int j=1;j<=temp;j++){//j代表列 
				a[i][j]=a[i-temp][j]+temp;
			} 
		} 
		for(int i=1;i<=temp;i++){//填写右上角的元素  i代表行 
			for(int j=temp+1;j<=n;j++){//j代表列 
				a[i][j]=a[i][j-temp]+temp; 
			}
		}
		for(int i=temp+1;i<=n;i++){//填写右下角的元素 i代表行 
			for(int j=temp+1;j<=n;j++){//j代表列 
				a[i][j]=a[i-temp][j-temp];
			} 
		}
	}
}

ai其实很简单

关注

12
点赞
踩
1

收藏

觉得还不错? 一键收藏
6
评论
算法分析：分治法。

算法设计：分治法在显示中，分而治之往往是将大片区域分成小块区域治理，算法中往往用递归来解决分治问题。1.## 分治算法的设计思想对于一个规模为n的问题，当问题可以很容易直接解决，则可以直接解决该问题。但当难以解决该问题时，可以将该问题分解为k个规模较小的子问题，这些子问题之间相互独立且与原问题形式相同，递归的解决这些子问题，最终将子问题合并得到原问题的解。2.分治法的解题步骤分解：将要解决的大问题分解成若干个规模更小的子问题，且这些子问题相互之间独立，与原问题形式相同。治理：由于子问题与原
复制链接

扫一扫