【数据结构与算法】自学笔记

复杂度分析

大$O$记号

在问题规模足够大后，计算成本如何增长？（更侧重整体增长趋势）

T(n):需执行的基本操作次数
T(n)=$O$( f(n) )
if $\exists$ c > 0 , 当 n >> 2 后 , 有T(n) < c$\cdot$f(n)

例：T(n)=$\sqrt{5n\cdot [3n\cdot (n+2)+4]+6}$ 对其简化

$\sqrt{5n\cdot [3n\cdot (n+2)+4]+6}$ \quad // 2–>n

\quad < $\sqrt{5n\cdot [6n^2+4]+6}$ \quad \quad \quad \quad // 4–>$n^2$

\quad < $\sqrt{35n^3+6}$ \quad \quad \quad \quad \quad \quad \quad \quad // 6–>$n^3$

\quad 6$\cdot$ $n^{1.5}$ = $O$ ( $n^{1.5}$)

与T(n)相比，f(n)更为简洁，但依然反应前者的增长趋势

• 常系数可忽略：$O$( f(n) ) = $O$( c$\times$f(n) )
• 低次项可忽略：$O$( $n^a+n^b$ ) = $O$($n^a$) , a > b > 0
  
  

大$\Omega$记号和大$\Theta$记号

• T(n) = $\Omega$( f(n) ) :
  $\exists$ c > 0 , 当 n >> 2 后 , 有T(n) > c$\cdot$f(n)
• T(n) = $\Theta$( f(n) ) :
  $\exists$ $c_1$ > $c_2$ > 0 , 当 n >> 2 后 , 有 $c_1$$\cdot$ f(n) > T(n) > $c_2$$\cdot$ f(n)
  
  

常见的$O$()

$O$(1)

常数
      2 = 2013 = 2013 $\times$ 2013 = $O$(1) , 甚至 $2013^{2013}$ = $O$(1)

这类算法的效率最高

$O$($lo{g}^{c}n$)

对数
      lnn  |  lgn  |  $lo{g}_{100}n$  |  $lo{g}_{2013}n$

常底数无所谓
      $\forall$ a , b > 0 , $lo{g}_{a}n$ = $lo{g}_{a}b$ $\cdot$ $lo{g}_{b}n$ = $\Theta$($lo{g}_{b}n$)

常数次幂无所谓
      $\forall$ c > 0 , $log{n}^c$ = c $\cdot$ logn = $\Theta$(log n)

对数多项式
      123*$lo{g}^{321}n$ + $lo{g}^{105}(n^2-n+1)$ = $\Theta$($lo{g}^{105}n$)

这类算法非常有效，复杂度无限接近于常数
      $\forall$ c > 0 , logn = $O$($n^c$)

$O$($n^c$)

一般的：$a_k{n}^k+a_{k-1}{n}^{k-1}+...+a_{1}n+a_0=O(n^k),a_k>0$

很明显，这是一种多项式的形式
例如：
$100n+200=O(n)$
$(100n-500)(20n^2-300n+2013)=O(n\times n^2)=O(n^3)$
$(2013n^2-20)/(1999n-1)=O(n^2/n)=O(n)$
$[(n^{2013}-24n^{2009}{)}^{1/3}+512n^{567}-1978n^{123}{]}^{1/11}=O(n^{61})$

线性复杂度：所有$O(n)$类函数

这类算法的效率通常认为已可令人满意了

$O$($2^n$)

指数：$T(n)=a^n$

$c>0,n^c=O(2^n)//e^n=1+n+n^2/2!+n^3/3!+n^4/4!+...$
            $n^{1000}=O(1.0000001^n)=O(2^n)$
            $1.0000001^n=\Omega (n^{1000})$

这类算法的计算成本增长极快，通常被认为不可忍受

从$O(n^c)$到$O(2^n)$，是从有效算法到无效算法的分水岭，有些问题的$O(2^n)$算法往往显而易见，但设计出$O(n^c)$算法却极其不易，甚至有时注定地只能是徒劳无功

例如 2-Subset 问题
问题描述：
     S包含n个正整数，$\sum S=2m$
     S是否有子集，满足$\sum T=m$
问题分析：简而言之，S集合内n个整数能否被恰好分成两部分，要求元素的个数不一定相同，但两部分的总和应相同
直觉算法：逐一枚举S的每一子集，并统计其中元素的总和
定理：$|2^s|=2^{|s|}=2^n$
显而易见 ，直觉算法需要迭代2轮，并（在最坏情况下）至少需要花费很多时间——不堪理想！

那是否可以进行优化？
答：2-Subset is NP-complete（无法优化）
就目前的计算模型而言，不存在可在多项式时间内回答此问题的算法，即上述的直觉算法已属最优

$O()$图像

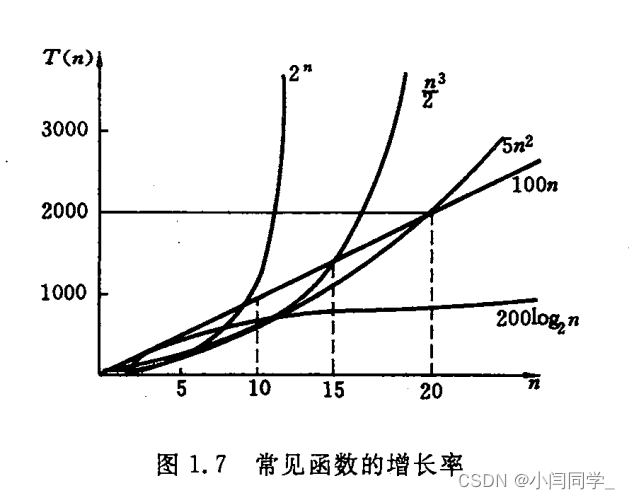
算法分析

两个主要任务 = 正确性（不变性$\times$单调性）+ 复杂度

关键在于复杂度的分析！

复杂度分析的主要方法：

• 迭代：级数求和
• 递归：递归跟踪 + 递推方程
• 猜测 + 验证

级数

• 算术级数：与末项平方同阶
  $T(n)=1+2+...+n=n(n+1)/2=O(n^2)$

• 幂方级数：比幂次高出一阶
  $T_2(n)=1^2+2^2+3^2+...+n^2=n(n+1)(2n+1)/6=O(n^3)$
  $T_3(n)=1^3+2^3+3^3+...+n^3=n^2(n+1{)}^2/4=O(n^4)$
  $T_4(n)=1^4+2^4+3^4+...+n^4=n(n+1)(2n+1)(3n^2+3n-1)/30=O(n^5)$

• 几何级数（ a>1 ）：与末项同阶
  $T_a(n)=a^0+a^1+...+a^n=(a^{n+1}-1)/(a-1)=O(a^n)$

• 收敛级数
  $1/1/2+1/2/3+1/3/4+...+1/(n-1)/n=1-1/n=O(1)$
  $1+1/2^2+...+1/n^2<1+1/2^2+...={\pi }^2/6$=O(1)
  $1/3+1/7+1/8+1/15+1/24+1/31+1/35+...=1=O(1)$

• 调和级数
  $h(n)=1+1/2+1/3+...+1/n=\Theta (logn)$

• 对数级数
  $log1+log2+log3+...+logn=log(n!)=\Theta (nlogn)$

循环和级数

————————————————————————

for(int i=0;i<n;i++)
for(int j=0;j<n;j++)

算数级数：
${\Sigma }_{i=0}^{n-1}n=n+n+...+n=n\ast n=O(n^2)$

可以把这个过程想象为点到线再到面的过程，i=0,j=0为第一个点，j++就是点到线的过程，然后i++就是线到面的过程；

————————————————————————

for(int i=0;i<n;i++)
for(int j=0;j<i;j++)

算数级数：
${\Sigma }_{i=0}^{n-1}i=0+1+...+(n-1)=n(n-1)/2=O(n^2)$

————————————————————————

for(int i=0;i<n;i++)
for(int j=0;j<i;j+=2013)

同理，也是算数级数；

————————————————————————

for(int i=1;i<n;i<<=1)
for(int j=0;j<i;j++)

几何级数：
$1+2+4+...+2^{\lfloor lo{g}_2(n-1)\rfloor }$
$={\Sigma }_{k=0}^{\lfloor lo{g}_2(n-1)\rfloor }{2}^k//（让k=lon{g}_{2}i）$
$=2^{\lfloor lo{g}_{2}n\rfloor }-1$
$=O(n)$

取非极端元素

问题：给定整数子集S，$|S|=n\ge 3$
           找出元素$a\in S,a\ne man(S)且a\ne ma\in (S)$

算法：

• 从S中任取三个元素{ x，y，z }

     //若s以2数组形式给出，不妨取前三个
     //由于s是集合，这三个元素必然互异

• 确定并排除其中的 最小，最大者

      //不妨设$x=max(x,y,z),y=min(x,y,z)$

• 输出剩下的元素 z

结论：无论输入规模n多大，上述算法需要执行的时间都不变
           $T(n)=常数=O(1)=\Omega (1)=\Theta (1)$

起泡排序

问题：给定n个整数，将它们按（非降）序排序
观察：有序/无序序列中，任意/总有一对相邻元素顺序/逆序
算法：扫描交换
           依次比较每一对相邻原色，如有必要，交换之，若整趟都没有进行交换，则排序完成；否则，再做一趟扫描交换

void bubblesort(int A[],int n)
{
    for(bool sorted = false;(sorted=!sorted);n--)//逐趟扫描交换，直至完全有序
    {
        for(int i=1;i<n;i++)//自左向右，逐对检查A[0,n]内各相邻元素
        {
            if(A[i-1]>A[i])//若逆序
            {
                swap(A[i-1],A[i]);//交换
                sorted = false;//清除（全局）有序标志
            }
        }
    }
}

分析：该算法必然会结束吗？至少需要迭代多少趟？

• 不变性：经 k 轮扫描交换后，最大的 k 个元素必然就位

        例如，按照要求给数组 A[ ] = {5，2，7，4，6，3，1}进行非递减的起泡排序，则第1轮扫描交换后，7这个元素一定在数组的最后一个位置，即 A[6] ；第2轮扫描交换后，6这个元素一定在 A[5] ，依次类推

• 单调性：经 k 轮扫描交换后，问题规模缩减至 n-k

       根据不变性，每一轮扫描交换后，总有一个元素确定好位置，则对于下一轮扫描交换来说，未确定位置的元素数量一定减一，即问题规模缩减至 n-k

• 正确性：经至多 n 趟扫描后，算法必然终止，且能给出正确解答

迭代和递归

数组求和【迭代】

问题：计算任意n个整数之和
实现：逐一取出每个元素，累加之

int SumI(int A[],int n){
    int sum=0;//o(1)
    for(int i=0;i<n;i++)//o(n)
        sum+=A[i];//o(1)
    return sum;//o(1)
 }

无论A[ ]内容如何，都有：
$T(n)=1+n\ast 1+1=n+2=O(n)=\Omega (n)=\Theta (n)$

减而治之

为求解一个大规模的问题，可以将其划分为两个子问题：其一平凡，另一规模缩减；分别求解子问题，由子问题的解，得到原问题的解。

数组求和【线性递归】【减而治之】

sum(int A[],int n){
    return
        (n<1)?0:sum(A,n-1)+A[n-1];
}

递归跟踪分析：检查每个递归实例，累计所需时间（调用语句本身，计入对应的子实例），其总和即算法执行时间；
本例中，单个递归实例自身只需$O(1)$时间
$T(n)=O(1)\ast (n+1)=O(n)$

从递推角度看，为求解sum(A , n)，需递归求解规模为n-1的问题sum()A , n-1)，再累加上A[n-1]；递归基：sum(A , 0);

递推方程
$T(n)=T(n-1)+o(1)$
$T(0)=O(1)$

求解
$T(n)-n=T(n-1)-(n-1)=...$
                  $=T(2)-2$
                  $=T(1)-1$
                  $=T(0)$
$T(n)=O(1)+n=O(n)$

数组倒置【减而治之】

任给数组A[0 , n)，将其前后颠倒

统一接口：

void reverse(int* A,int low,int high);

递归版

if(low < high){//问题规模的奇偶性不变，需要两个递归基
    swap(A[low],A[high]);
    reverse(A,low+1,high-1);
}

迭代版

while(low < high){
    swap(A[low++],A[high--]);
}

分而治之

为求解一个大规模的问题，可以将其划分若干（通常两个）子问题，规模大体相当，分别求解子问题，由子问题的解，得到原问题的解。

数组求和【二分递归】【分而治之】

sum(int A[],int low,int high){
    if(low == high) return A[1ow];
    int middle=(low + high) >> 1;
    return sum(A,low,high) + sum(A,middle+1,high);
}//入口形式为sum(A,0,n-1)

$T(n)=各层递归实例所需时间之和$
           $=O(1)\ast (2^0+2^1+2^2+2^{logn})$
           $=O(1)\ast (2^{logn+1}-1)=O(n)$

从递推角度看，为求解sun(A, low, high)，需递归求解sum(A, low, middle)和sum(A, middle+1, high)，进而将子问题的解累加；递归基：sum(A, low, low);

递推关系
$T(n)=2\ast T(n/2)+o(1)$
$T(1)=O(1)$

求解
$T(n)$          $=2\ast T(n/2)+c_1$
$T(n)+c_1=2\ast (T(n/2)+c_1)=2^2\ast (T(n/4)+c_1)$
                    $=...$
                    $=2^{logn}(T(1)+c_1)=n\ast (c_2+c_1)$
$T(n)$           $=(c_1+c_2)n-c_1=O(n)$

动态规划

所谓的动态规划，其实可以理解为，通过递归找出算法的本质，并且给出一个初步的解，再将其等效得转化为迭代的形式。

FIB()

递归：$fib(n)=fib(n-1)+fib(n-2):0,1,1,2,3,5,\mathrm{8......}$

int fib(n)
{
    return (2 > n) ? n : fib(n-1)+fib(n-2);
}  

复杂度分析：
$T(0)=1,T(1)=1,T(n)=T(n-1)+T(n+1)+1,(n>1)$
$令S(n)=[T(n)+1]/2$
$则S(0)=1=fib(1),S(1)=1=fib(2)$
$故S(n)=S(n-1)+S(n-2)=fib(n+1)$
$T(n)=2\ast S(n)-1=2\ast fib(n+1)-1=O(2\ast fib(n+1))=O(n^2)$

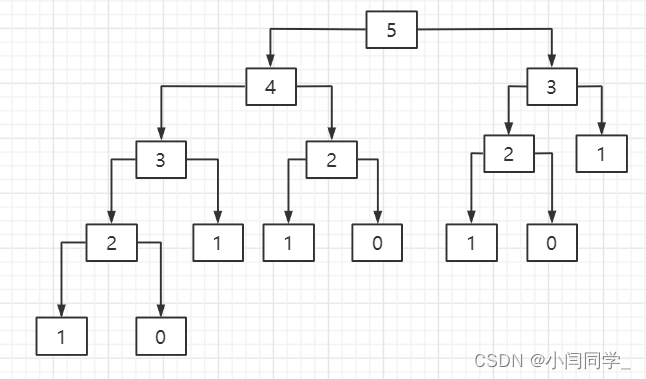
递归版 fib() 低效地根源在于，各递归实例均被大量重复地调用

解决方法A（ 记忆化 ）
将已计算过的实例地结果制表备查

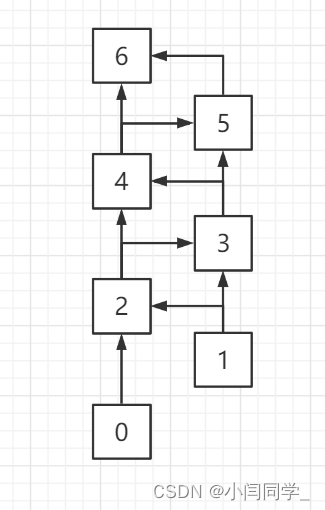
解决方法B（ 动态规划 ）
颠倒计算方向：由自顶而下递归，为自底而上迭代

f=0;//fib(0)
g=1;//fib(1)
while(0 < n--)
{
    g=g+f;
    f=g-f;
}
return g;

$T(n)=O(n)，且仅只需O(1)空间$

LCS

子序列：由序列中若干字符，按原想对次序构成
最长公共子序列：两个序列公共子序列中的最长者（可能有多个，也可能有歧义）

递归
对于序列A[0,n]和B[0,m]，即LCS(A,B)就有三种情况

1. 若n=-1或m=-1，则取作空序列(‘’‘’) //递归基
2. 若A[n]=‘X’=B[m]，则取作$LCS(A[0,n),B[0,m)){+}^{\prime }{X}^{\prime }$ //减而治之
3. A[n]!=B[m]，则在$LCS(A[0,n],B[0,m))与LCS(A[0,n),B[0,m])$中取更长者 //分而治之