【Pytorch学习笔记】模型模块03——常用网络层（2）

Normaliation Layers

归一化层是深度学习中的重要组件，用于标准化数据分布，加速训练过程并提高模型性能。

1. BatchNorm2d

**基本概念：**对小批量数据在通道维度上进行归一化

计算公式：

y = (x - E[x]) / sqrt(Var[x] + ε) * γ + β

公式解释：

这个BatchNorm2d的公式中各参数含义如下：

• x：输入数据
• E[x]：批次数据的均值
• Var[x]：批次数据的方差
• ε (epsilon)：一个很小的数值，用于数值稳定性，防止除零
• γ (gamma)：可学习的缩放参数
• β (beta)：可学习的偏移参数

这个公式的作用是：

• 首先将数据标准化到均值为0，方差为1的分布 ((x - E[x]) / sqrt(Var[x] + ε))
• 然后通过γ和β参数进行缩放和偏移，使网络能够学习到最适合的数据分布

BatchNorm2d的意义在于：对小批量数据在通道维度上进行归一化，这样可以：

• 加速网络训练收敛
• 减轻内部协变量偏移问题
• 允许使用更大的学习率
• 具有一定的正则化效果

参数：

• num_features：输入特征数（通道数）
• eps：添加到分母的小值（默认：1e-5）
• momentum：用于计算运行平均值的动量（默认：0.1）

# BatchNorm2d示例
class ConvBNReLU(nn.Module):
    def __init__(self, in_channels, out_channels):
        super().__init__()
        self.conv = nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1)
        self.bn = nn.BatchNorm2d(out_channels)
        self.relu = nn.ReLU()
    
    def forward(self, x):
        return self.relu(self.bn(self.conv(x)))

2. LayerNorm

**基本概念：**在最后几个维度上对输入进行归一化

主要参数：

• normalized_shape：要归一化的维度的形状
• eps：数值稳定性的小值（默认：1e-5）

# LayerNorm示例
layer_norm = nn.LayerNorm(normalized_shape=[64, 32])
input = torch.randn(20, 64, 32)  # batch_size=20
output = layer_norm(input)

3. InstanceNorm2d

**基本概念：**对每个样本的每个通道独立进行归一化

主要参数：

• num_features：输入特征数（通道数）
• eps：数值稳定性参数
• affine：是否学习仿射参数

# InstanceNorm2d示例
instance_norm = nn.InstanceNorm2d(num_features=64, affine=True)
input = torch.randn(20, 64, 32, 32)  # batch_size=20, channels=64
output = instance_norm(input)

4. GroupNorm

**基本概念：**将通道分组后进行归一化

主要参数：

• num_groups：分组数量
• num_channels：输入通道数

# GroupNorm示例
group_norm = nn.GroupNorm(num_groups=8, num_channels=64)
input = torch.randn(20, 64, 32, 32)
output = group_norm(input)

5. 综合应用示例

class NormalizationExample(nn.Module):
    def __init__(self, channels):
        super().__init__()
        self.batch_norm = nn.BatchNorm2d(channels)
        self.layer_norm = nn.LayerNorm([channels, 32, 32])
        self.instance_norm = nn.InstanceNorm2d(channels)
        self.group_norm = nn.GroupNorm(8, channels)
        
    def forward(self, x):
        # 不同归一化方法的效果
        batch_norm_out = self.batch_norm(x)
        layer_norm_out = self.layer_norm(x)
        instance_norm_out = self.instance_norm(x)
        group_norm_out = self.group_norm(x)
        
        return {
            'batch_norm': batch_norm_out,
            'layer_norm': layer_norm_out,
            'instance_norm': instance_norm_out,
            'group_norm': group_norm_out
        }

6. 使用建议

• BatchNorm适用于大批量训练，对小批量效果较差
• LayerNorm适用于NLP任务和Transformer架构
• InstanceNorm常用于风格迁移等图像生成任务
• GroupNorm是BatchNorm和LayerNorm的折中方案，适用于小批量训练

7. 注意事项

• 评估模式下，BatchNorm使用运行统计量而非批次统计量
• 选择合适的eps值对数值稳定性很重要
• 不同归一化层的选择应考虑具体任务特点
• 注意训练和推理时的行为差异

Dropout layers

**基本概念：**Dropout是一种正则化技术，通过在训练时随机"丢弃"一部分神经元来防止过拟合。

计算公式：

output = input * mask / (1 - p)
# 其中mask是一个由0和1组成的随机张量，p是丢弃概率

主要参数：

• p：丢弃概率（默认0.5）
• inplace：是否直接修改输入张量（默认False）

1. nn.Dropout

最基础的Dropout层，用于全连接层：

# Dropout示例
class SimpleNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear1 = nn.Linear(100, 50)
        self.dropout = nn.Dropout(p=0.5)
        self.linear2 = nn.Linear(50, 10)
    
    def forward(self, x):
        x = F.relu(self.linear1(x))
        x = self.dropout(x)  # 训练时随机丢弃50%的神经元
        return self.linear2(x)

2. nn.Dropout2d

用于卷积层的特征图，按通道随机丢弃：

# Dropout2d示例
class ConvNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv = nn.Conv2d(3, 64, 3)
        self.dropout2d = nn.Dropout2d(p=0.2)
    
    def forward(self, x):
        x = F.relu(self.conv(x))
        return self.dropout2d(x)  # 按通道随机丢弃

3. nn.Dropout3d

用于3D卷积的特征图，常用于视频或3D医学图像处理：

# Dropout3d示例
class Conv3DNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv3d = nn.Conv3d(1, 16, 3)
        self.dropout3d = nn.Dropout3d(p=0.3)
    
    def forward(self, x):
        x = F.relu(self.conv3d(x))
        return self.dropout3d(x)

4. 使用注意事项

• 训练时启用，评估时自动禁用（model.eval()）
• 丢弃概率p不宜过大，通常在0.2-0.5之间
• 通常在全连接层之后使用
• 对于卷积网络，推荐使用Dropout2d而不是普通Dropout

5. 综合应用示例

class ComplexNet(nn.Module):
    def __init__(self):
        super().__init__()
        # 卷积层部分
        self.conv = nn.Conv2d(3, 64, 3)
        self.dropout2d = nn.Dropout2d(0.2)
        
        # 全连接层部分
        self.fc1 = nn.Linear(64 * 30 * 30, 512)
        self.dropout = nn.Dropout(0.5)
        self.fc2 = nn.Linear(512, 10)
    
    def forward(self, x):
        # 卷积层的Dropout
        x = F.relu(self.conv(x))
        x = self.dropout2d(x)
        
        # 全连接层的Dropout
        x = x.view(x.size(0), -1)
        x = F.relu(self.fc1(x))
        x = self.dropout(x)
        x = self.fc2(x)
        
        return x

“x = x.view(x.size(0), -1)”这行代码的作用是重塑（reshape）张量的维度：

• x.size(0) 保持批次大小（batch size）不变
• -1 表示自动计算剩余维度，将所有特征展平成一维向量

示例解释：

# 假设输入张量 x 的形状是 [32, 64, 30, 30]
# 其中：32是批次大小，64是通道数，30x30是特征图大小

x = x.view(x.size(0), -1)
# 输出张量形状变为 [32, 57600]
# 57600 = 64 * 30 * 30

这种操作通常用在卷积层到全连接层的过渡处，因为全连接层需要一维输入。

Alpha Dropout

**基本概念：**Alpha Dropout是一种特殊的Dropout变体，专门设计用于自归一化神经网络（如SELU激活函数）。它的特点是在应用dropout时保持输入均值和方差。先介绍SELU激活函数。

SELU (Scaled Exponential Linear Unit) 激活函数

**基本概念：**SELU是一种自归一化激活函数，它能够自动将神经网络层的输出归一化到固定的均值和方差。

数学表达式：

selu(x) = scale * (max(0, x) + min(0, alpha * (exp(x) - 1)))
# 其中 scale ≈ 1.0507 和 alpha ≈ 1.6733 是预定义的常数

特点：

• 自归一化：无需额外的批量归一化层
• 稳定性：有助于防止梯度消失和梯度爆炸
• 快速收敛：训练过程更加稳定和高效

使用场景：

• 深层前馈神经网络
• 需要自归一化特性的网络架构
• 与Alpha Dropout配合使用效果更佳

# SELU激活函数使用示例
class SELUNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(100, 50)
        self.fc2 = nn.Linear(50, 10)
    
    def forward(self, x):
        x = F.selu(self.fc1(x))
        x = F.selu(self.fc2(x))
        return x

**Alpha Dropout计算公式：**Alpha Dropout将输入值随机置为负饱和值（通常约为-1.7580），同时保持均值和方差不变。

主要参数：

• p：丢弃概率（默认0.5）
• inplace：是否直接修改输入张量（默认False）

1. 基本使用示例

class AlphaDropoutNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear1 = nn.Linear(100, 50)
        self.alpha_dropout = nn.AlphaDropout(p=0.3)
        self.linear2 = nn.Linear(50, 10)
    
    def forward(self, x):
        x = F.selu(self.linear1(x))
        x = self.alpha_dropout(x)
        return self.linear2(x)

2. 使用注意事项

• 通常与SELU激活函数配合使用
• 训练时自动启用，评估时自动禁用
• 适用于需要自归一化特性的深度神经网络
• 丢弃概率建议设置在0.1-0.3之间

3. 完整应用示例

class SelfNormalizingNet(nn.Module):
    def __init__(self, input_size, hidden_size, output_size, dropout_p=0.2):
        super().__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.alpha_dropout1 = nn.AlphaDropout(p=dropout_p)
        self.fc2 = nn.Linear(hidden_size, hidden_size)
        self.alpha_dropout2 = nn.AlphaDropout(p=dropout_p)
        self.fc3 = nn.Linear(hidden_size, output_size)
        
    def forward(self, x):
        x = F.selu(self.fc1(x))
        x = self.alpha_dropout1(x)
        x = F.selu(self.fc2(x))
        x = self.alpha_dropout2(x)
        x = self.fc3(x)
        return x

# 创建模型实例
model = SelfNormalizingNet(
    input_size=784,
    hidden_size=512,
    output_size=10,
    dropout_p=0.2
)

优势和特点：

• 保持网络的自归一化特性
• 减少内部协变量偏移
• 特别适合深层神经网络
• 有助于保持网络训练的稳定性

Non-linear Layers

非线性层是神经网络中的重要组成部分，它们引入非线性变换，使网络能够学习复杂的模式。

1.Sigmoid

计算公式： sigmoid(x) = 1 / (1 + e^(-x))

• 输出范围：(0, 1)
• 常用于二分类问题的输出层

class SigmoidExample(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(10, 1)
        self.sigmoid = nn.Sigmoid()
    
    def forward(self, x):
        x = self.linear(x)
        return self.sigmoid(x)  # 或使用 F.sigmoid(x)

2. Tanh

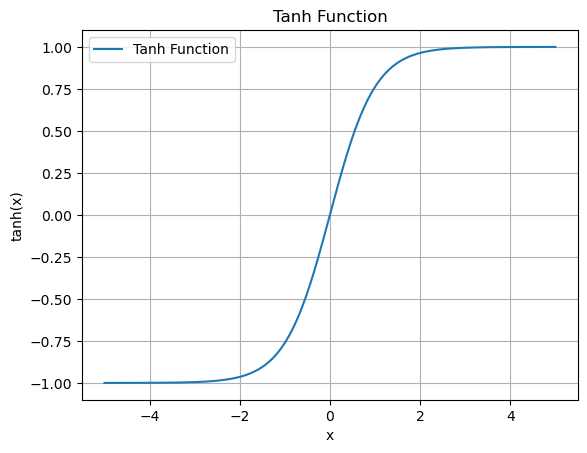
计算公式： tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))

• 输出范围：(-1, 1)
• 在RNN和LSTM中经常使用

class TanhExample(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(10, 5)
        self.tanh = nn.Tanh()
    
    def forward(self, x):
        x = self.linear(x)
        return self.tanh(x)  # 或使用 F.tanh(x)

3. ReLU (Rectified Linear Unit)

计算公式： ReLU(x) = max(0, x)

• 最常用的激活函数
• 解决了梯度消失问题
• 计算效率高

class ReLUExample(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(20, 10)
        self.relu = nn.ReLU()
        # 可选参数
        self.relu_with_params = nn.ReLU(inplace=True)  # inplace=True可节省内存
    
    def forward(self, x):
        x = self.linear(x)
        return self.relu(x)  # 或使用 F.relu(x)

4. PReLU (Parametric ReLU)

计算公式： PReLU(x) = max(0, x) + a * min(0, x)

其中a是可学习的参数

class PReLUExample(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(10, 5)
        self.prelu = nn.PReLU()  # 默认为每个通道学习一个参数
        # 可选：指定参数数量
        self.prelu_params = nn.PReLU(num_parameters=1)  # 所有通道共享同一参数
    
    def forward(self, x):
        x = self.linear(x)
        return self.prelu(x)

5. Softmax

计算公式： softmax(x_i) = exp(x_i) / Σ(exp(x_j))

主要特点：

• 将输入转换为概率分布（和为1的非负数）
• 常用于多分类问题的输出层
• 对数值敏感，需要注意数值稳定性

主要参数：

• dim：指定softmax运算的维度

class SoftmaxExample(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(100, 10)
        self.softmax = nn.Softmax(dim=1)  # dim=1表示在第二维度上进行softmax
    
    def forward(self, x):
        x = self.linear(x)
        return self.softmax(x)  # 或使用 F.softmax(x, dim=1)

# 实际应用中的完整示例
class MultiClassClassifier(nn.Module):
    def __init__(self, input_size, hidden_size, num_classes):
        super().__init__()
        self.layer1 = nn.Linear(input_size, hidden_size)
        self.layer2 = nn.Linear(hidden_size, hidden_size)
        self.layer3 = nn.Linear(hidden_size, num_classes)
        self.relu = nn.ReLU()
        self.softmax = nn.Softmax(dim=1)
    
    def forward(self, x):
        x = self.relu(self.layer1(x))
        x = self.relu(self.layer2(x))
        x = self.layer3(x)
        return self.softmax(x)

注意事项：

• 在使用交叉熵损失函数（nn.CrossEntropyLoss）时，不需要显式添加softmax层，因为损失函数内部已包含
• softmax对数值差异很敏感，可能导致数值溢出，建议先进行归一化
• 在实际应用中，通常在训练时使用log_softmax配合NLLLoss，这样数值更稳定