算法设计与分析-笔记-第1章-算法概述（理清5种渐近分析的记号，学会算法复杂性分析，区分P、NP、NPC、NP-Hard问题）

第1章 算法概述

（一）算法与程序

1.算法

算法是解决问题的一种方法或过程

算法是由若干条指令组成的有穷序列

算法满足：

​ ①输入：有零个或多个输入

​ ②输出：至少有一个输出

​ ③确定性：每条指令是清晰无歧义的

​ ④有限性：每条指令执行次数和执行时间是有限的

2.程序

程序是算法用某种程序设计语言的具体实现

算法必须满足①~④，而程序不一定满足④

操作系统是在无限循环中执行的程序而不是算法，操作系统的各种任务由特定的子程序实现，子程序既是程序也是算法

数据结构+算法=程序

（二）算法复杂性分析

1.算法的复杂性

算法复杂性=算法所需要的计算机资源

$n$：问题的规模、输入数据的大小

时间复杂度$T(n)$：需要的时间资源，对应CPU

空间复杂度$S(n)$：需要的空间资源，对应内存

2.算法的渐进复杂性

当$n\to \infty$，有$\frac{T(n)-t(n)}{T(n)}\to 0$，称$t(n)$是$T(n)$的渐进性态，为算法的渐进复杂性

数学上，$t(n)$是$T(n)$的渐进表达式，为$T(n)$略去低阶项留下的主项（$n\to \infty$时，变化最快的项）

例如：$T(n)=4N^2+3N-1$，则$t(n)=4n^2$

3.算法的时间复杂性

$I$：问题的规模为$n$的实例 $p(I)$：实例$I$出现的概率

最坏情况下的时间复杂性

​ T m a x ( n ) = m a x { T ( I ) ∣ s i z e ( I ) = n } T_{max}(n)=max\{T(I)|size(I)=n\} Tmax​(n)=max{T(I)∣size(I)=n}

最好情况下的时间复杂性

​ T m i n ( n ) = m i n { T ( I ) ∣ s i z e ( I ) = n } T_{min}(n)=min\{T(I)|size(I)=n\} Tmin​(n)=min{T(I)∣size(I)=n}

平均情况下的时间复杂性

​ $T_{avg}(n)={\sum }_{size(I)=n}p(I）T（I）$

4.渐近分析的记号

（1）渐近上界记号$\mathrm{O}$

O ( g ( n ) ) = { f ( n ) ∣ 存 在 正 常 数 c 和 n 0 使 得 对 所 有 n ≥ n 0 有 ： 0 ≤ f ( n ) ≤ c g ( n ) } \Omicron(g(n))=\{f(n)|存在正常数c和n_0使得对所有n\geq{n}_0有：0\leq{f(n)}\leq{cg(n)}\} O(g(n))={f(n)∣存在正常数c和n0​使得对所有n≥n0​有：0≤f(n)≤cg(n)}

如：$3N+10=\mathrm{O}(N)$

如：$4N^2+3N-1=\mathrm{O}(N^2)$

（2）渐近下界记号$\Omega$

Ω ( g ( n ) ) = { f ( n ) ∣ 存 在 正 常 数 c 和 n 0 使 得 对 所 有 n ≥ n 0 有 ： 0 ≤ c g ( n ) ) ≤ f ( n ) } \Omega(g(n))=\{f(n)|存在正常数c和n_0使得对所有n\geq{n}_0有：0\leq{cg(n))}\leq{f(n)}\} Ω(g(n))={f(n)∣存在正常数c和n0​使得对所有n≥n0​有：0≤cg(n))≤f(n)}

如：$3N+10=\Omega (1)$

如：$4N^2+3N-1=\Omega (N^2)$

（3）非紧上界记号$o$

ο ( g ( n ) ) = { f ( n ) ∣ 对 于 任 何 正 常 数 c ， 存 在 正 数 n 0 使 得 对 所 有 n ≥ n 0 有 ： 0 ≤ f ( n ) ≤ c g ( n ) } \omicron(g(n))=\{f(n)|对于任何正常数c，存在正数n_0使得对所有n\geq{n}_0有：0\leq{f(n)}\leq{cg(n)}\} ο(g(n))={f(n)∣对于任何正常数c，存在正数n0​使得对所有n≥n0​有：0≤f(n)≤cg(n)}

等价于当$n\to \infty$有$\frac{f(n)}{g(n)}\to 0$

如：$4N^2+3N-1=o(N^3)$

（4）非紧下界记号$\omega$

ω ( g ( n ) ) = { f ( n ) ∣ 对 于 任 何 正 常 数 c ， 存 在 正 数 n 0 使 得 对 所 有 n ≥ n 0 有 ： 0 ≤ c g ( n ) ) ≤ f ( n ) } \omega(g(n))=\{f(n)|对于任何正常数c，存在正数n_0使得对所有n\geq{n}_0有：0\leq{cg(n))}\leq{f(n)}\} ω(g(n))={f(n)∣对于任何正常数c，存在正数n0​使得对所有n≥n0​有：0≤cg(n))≤f(n)}

等价于当$n\to \infty$有$\frac{f(n)}{g(n)}\to \infty$

如：$4N^2+3N-1=\omega (N)$

（5）紧渐近界记号$\Theta$

Θ ( g ( n ) ) = { f ( n ) ∣ 存 在 正 常 数 c 1 、 c 2 和 n 0 使 得 对 所 有 n ≥ n 0 有 ： c 1 g ( n ) ≤ f ( n ) ≤ c 2 g ( n ) } \Theta(g(n))=\{f(n)|存在正常数c_1、c_2和n_0使得对所有n\geq{n}_0有：c_1g(n)\leq{f(n)}\leq{c_2g(n)}\} Θ(g(n))={f(n)∣存在正常数c1​、c2​和n0​使得对所有n≥n0​有：c1​g(n)≤f(n)≤c2​g(n)}

$\Theta (g(n))=\mathrm{O}(g(n))\bigcap \Omega (g(n))$

如：$4N^2+3N-1=\Theta (N^2)$

5.渐近分析记号在等式和不等式中的意义

$f(n)=\Theta (g(n))\iff f(n)\in \Theta (g(n))$

一般来说，$\Theta (g(n))$表示$\Theta (g(n))$中的某个函数

如：$4n^2+3n-1=4n^2+\Theta (n)$表示$4n^2+3n-1=4n^2+f(n)$，$f(n)$是$\Theta (n)$中的某个函数

$\mathrm{O}、o、\Omega 、\omega$同理

6.渐近分析中函数比较

$f(n)=\mathrm{O}(g(n))\approx a\le b$

$f(n)=\Omega (g(n))\approx a\ge b$

$f(n)=o(g(n))\approx a<b$

$f(n)=\omega (g(n))\approx a>b$

$f(n)=\Theta (g(n))\approx a=b$

7.渐近分析记号的性质

（1）传递性

$f(n)=\Theta (g(n)),g(n)=\Theta (h(n))\Rightarrow f(n)=\Theta (h(n))$

$f(n)=\mathrm{O}(g(n)),g(n)=\mathrm{O}(h(n))\Rightarrow f(n)=\mathrm{O}(h(n))$

$f(n)=\Omega (g(n)),g(n)=\Omega (h(n))\Rightarrow f(n)=\Omega (h(n))$

$f(n)=o(g(n)),g(n)=o(h(n))\Rightarrow f(n)=o(h(n))$

$f(n)=\omega (g(n)),g(n)=\omega (h(n))\Rightarrow f(n)=\omega (h(n))$

（2）反身性

$f(n)=\Theta (f(n))$

$f(n)=\mathrm{O}(f(n))$

$f(n)=\Omega (f(n))$

（3）对称性

$f(n)=\Theta (g(n))\iff g(n)=\Theta (f(n))$

（4）互对称性

$f(n)=\mathrm{O}(g(n))\iff g(n)=\Omega (f(n))$

$f(n)=o(g(n))\iff g(n)=\omega (f(n))$

（5）算术运算（以$\mathrm{O}$为例）

O ( f ( n ) ) + O ( g ( n ) ) = O ( m a x { f ( n ) , g ( n ) } ) \Omicron(f(n))+\Omicron(g(n))=\Omicron(max\{{f(n),g(n)}\}) O(f(n))+O(g(n))=O(max{f(n),g(n)})

$\mathrm{O}(f(n))+\mathrm{O}(g(n))=\mathrm{O}(f(n)+g(n))$

$\mathrm{O}(f(n))\ast \mathrm{O}(g(n))=\mathrm{O}(f(n)\ast g(n))$

$\mathrm{O}(cf(n)=\mathrm{O}(f(n))$

$g(n)=\mathrm{O}(f(n))\Rightarrow \mathrm{O}(f(n))+\mathrm{O}(g(n))=\mathrm{O}(f(n))$

8.渐近记号的关系

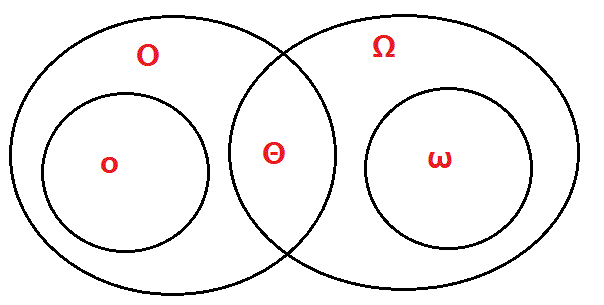
9.渐近关系的快速判断

$f(n)=\Theta (g(n))\iff \underset{n\to \infty }{\lim }\frac{f(n)}{g(n)}=c(f(n)与g(n)同阶)$

$f(n)=o(g(n))\iff \underset{n\to \infty }{\lim }\frac{f(n)}{g(n)}=0(f(n)比g(n)低阶)$

$f(n)=\omega (g(n))\iff \underset{n\to \infty }{\lim }\frac{f(n)}{g(n)}=\infty (f(n)比g(n)高阶)$

$f(n)=\mathrm{O}(g(n))\iff \mathrm{O}(g(n))为\Theta (g(n))和o(g(n))中阶数更低的那个$

$f(n)=\Omega (g(n))\iff \mathrm{O}(g(n))为\Theta (g(n))和\omega (g(n))中阶数更高的那个$

求渐近表达式的一般步骤：去除低阶项只保留最高阶项，再去掉最高级项的系数

10.常见的时间复杂度的渐近阶排序

$\mathrm{O}(n^{-1})<\mathrm{O}(1)<\mathrm{O}(logn)<\mathrm{O}(\sqrt{n})<\mathrm{O}(n)<\mathrm{O}(nlogn)<\mathrm{O}(n^2)<\mathrm{O}(n^3)<\mathrm{O}(2^n)<\mathrm{O}(n!)<\mathrm{O}(n^n)$

11.算法渐近复杂性分析中常用函数

（1）单调函数

单调递增：$m\le n\Rightarrow f(m)\le f(n)$

单调递减：$m\le n\Rightarrow f(m)\ge f(n)$

严格单调递增：$m<n\Rightarrow f(m)<f(n)$

严格单调递减：$m<n\Rightarrow f(m)>f(n)$

（2）取整函数

$x-1<\lfloor x\rfloor \le x\le \lceil x\rceil <x+1$

$\lfloor \frac{n}{2}\rfloor +\lceil \frac{n}{2}\rceil =n$

对于$n\ge 0,a,b>0$，有：

$\lceil \frac{\lceil \frac{n}{a}\rceil }{b}\rceil =\lceil \frac{n}{ab}\rceil$

$\lfloor \frac{\lfloor \frac{n}{a}\rfloor }{b}\rfloor =\lfloor \frac{n}{ab}\rfloor$

$\lceil \frac{a}{b}\rceil \le \frac{a+(b-1)}{b}$

$\lfloor \frac{a}{b}\rfloor \ge \frac{a-(b-1)}{b}$

（3）多项式函数

$p(n)=a_0+a_{1}n+a_2{n}^2+...+a_d{n}^d,a_d>0$

$p(n)=\Theta (n^d)$

$f(n)=\mathrm{O}(n^k)\iff f(n)有界$

$f(n)=\mathrm{O}(1)\iff f(n)\le c$

$k\ge d\Rightarrow p(n)=\mathrm{O}(n^k)$

$k\le d\Rightarrow p(n)=\Omega (n^k)$

$k>d\Rightarrow p(n)=o(n^k)$

$k<d\Rightarrow p(n)=\omega (n^k)$

（4）指数函数

$(a^m{)}^n=(a^n{)}^m=a^{mn}$

$a^m{a}^n=a^{m+n}$

$a>1,n^b=o(a^n)$

$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+...=\sum _{i=0}^{\infty }\frac{x^i}{i!}$

$|x|\le 1,1+x\le e^x\le 1+x+\Theta (x^2)$

$\underset{n\to \infty }{\lim }{(1+\frac{x}{n})}^n=e^x$

（5）对数函数

$\log n={\log }_{2}n,\lg n={\log }_{10}n,\ln n={\log }_{e}n$

$a>0,b>0,c>0:$

$a=b^{lo{g}_{b}a}$

$lo{g}_c(ab)=lo{g}_{c}a+lo{g}_{c}b$

$lo{g}_c(\frac{a}{b})=lo{g}_{c}a-lo{g}_{c}b$

$lo{g}_b(a^n)=nlo{g}_{b}a$

$lo{g}_b(a)=\frac{lo{g}_{c}a}{lo{g}_{c}b}$

$lo{g}_b(a)=\frac{1}{lo{g}_{a}b}$

$a^{lo{g}_{b}c}=c^{lo{g}_{b}a}$

$a>0,lo{g}^{b}n=o(n^a)$

$x>-1,\frac{x}{1+x}\le ln(1+x)\le x$

$|x|\le 1,ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+...$

（6）阶乘函数

$n!=1\times 2\times 3...\times n$

$n!=\{\begin{array}{l}1,n=1\\ n(n-1)!,n>1\end{array}$

$n!=o(n^n)$

$n!=\omega (2^n)$

（三）算法分析的基本法则

1.计算时间选择

（1）for/while循环

循环体内计算时间*循环次数

（2）嵌套循环

循环体内计算时间*所有循环次数

（3）顺序语句

各语句计算时间相加

（4）if-else语句

if语句计算时间和else语句计算时间的较大者

2.最优算法

问题的计算时间下界为$\Omega (f(n))$，则计算时间复杂性为$\mathrm{O}(f(n))$的算法是最优算法

如：排序问题的计算时间下界为$\Omega (nlogn)$，计算时间复杂性为$\mathrm{O}(nlogn)$（堆排序）的排序算法是最优算法

（四）NP完全性理论

1.P类问题与NP类问题

	说明
易处理的问题	需要多项式时间算法求解的问题
难处理的问题	需要超多项式时间才能求解的问题
不可解问题	任何计算机无论耗费多长时间都不能解决的问题
	如：图灵停机问题——不能给出一个判断任意一个图灵机是否停机的一般方法 同理还有： 理发师悖论：村里有个理发师，该理发师有条原则：村里的人如果不自己理发，理发师就给这个人理发，否则不给这个 人理发，那么理 发师能否给自己理发是不可解的。 停机测试悖论：计算机有个测试程序，该测试程序有条原则：计算机里的程序如果不递归调用自己，测试程序就调用它，否则不调它， 那么测试程序能否自己递归调用自己是不可解的。
非确定性问题	问题的答案无法直接计算得到，只能通过判断猜算的正确与否得到
	多项式非确定性问题：判断猜算正确与否的算法可以在多项式时间内算出来 完全多项式非确定性问题：该问题的所有可能答案能在多项式时间内进行正确与否的验算
	如：旅行售货员问题（TSP） G=(V,E)是一个带权图，图中各边的权为费用，周游路线是包含V中每个顶点的一条回路 最优化形式的TSP问题——在G中找出费用最小的周游线路——较难 判定形式的TSP问题——判断G中是否存在总费用不超过d的周游线路——较易
	非确定性算法：将问题分解为猜想和验证两个阶段 猜测：给出问题的一个猜想——非确定性 验证：验证猜测阶段给出解的正确性——确定性

P、NP、NPC、NP-Hard问题

	说明
P	可以在多项式时间解决的问题 （确定性计算模型下的易解问题类）
NP	目前无多项式时间解决的算法，但可以在多项式时间内验证候选答案是否正确 （NP类问题是非确定性计算模型下的易验证问题类）
NPC	①本身是NP问题 ②任何一个NP问题都可以在多项式时间规约到该问题
NP-Hard	①本身不能确定是NP问题 ②任何一个NP问题都可以在多项式时间规约到该问题

$P\subseteq NP$
$NPC\subseteq NP-Hard$

2.NP完全问题（NPC）

如果一个NP完全问题(NPC)能在多项式时间内得到解决，那么NP中的每一个问题都可以在多项式时间内求解

目前还没有一个NP完全问题(NPC)有多项式时间算法

3.一些典型的NP完全问题

4.NP完全问题的近似算法

（1）只对问题的特殊实例求解

（2）只求近似解

（3）用动态规划法或分支限界法求解

（4）用概率算法求解

（5）用启发式方法求解