算法分析一：基础知识

1. 主要概念

1.1 算法概念

1.1.1 算法的理解

定义：在解决问题时，按照某种机械步骤一定可以得到问题结果的处理过程，通俗说，算法指解决问题的方法或过程。
三要素：算法由操作、控制结构、数据结构三要素组成。
算法分析的目的：1.为了对算法的某些特定输入，估算该算法的内存空间和运行时间。2.为了建立衡量算法优劣的标准，用以比较同一类问题的不同算法。

1.1.2 算法的组成

输入：需要处理的数据
输出：算法执行完毕得到的结果
算法步骤：把输入转化为输出的步骤

1.1.3 算法步骤的表示

自然语言：不精确但直观
伪代码：精确且通用，但不能运行
代码：精确，可以运行，但没有通用性

1.1.4 算法设计

基本要求：正确性和可读性。

1.1.5 算法五大特性

1、输入：算法具有0个或多个输入
2、输出：算法至少有1个或多个输出
3、有穷性：算法在有限的步骤之后会自动结束而不会无线循环，并且每一个步骤可以在可接受的时间内完成
4、确定性：算法中的每一步都有确定的含义，不会出现二义性
5、可行性：算法的每一步都是可行的，也就是说每一步都能够执行有限的次数完成

1.1.6 算法效率

一个算法的优劣可以用时间复杂度和空间复杂度来衡量。

1.2 算法的复杂性

定义：是指算法在运行过程中所需要的时间和空间资源的多少，所需资源越多，算法复杂性越高。

1.2.1 算法的时间复杂度

一般情况下，算法中的基本操作语句的重复执行次数是问题规模 n 的某个函数，用 T(n)表示，若有某个辅 助函数 f(n)，使得当 n 趋近于无穷大时，T(n) / f(n) 的极限值为不等于零的常数，则称 f(n)是 T(n)的同数量级函数。 记作 T(n)=Ｏ( f(n) )，称Ｏ( f(n) ) 为算法的渐进时间复杂度，简称时间复杂度。

1.2.2 时间复杂度的分类

• 最坏情况下的时间复杂度
• 最好情况下的时间复杂度
• 平均情况下的时间复杂度

1.2.3 计算时间复杂度

主定理
递归树
递归方程

1.4 函数的渐近的界

1.4.1 符号

1.4.2 有关函数的渐近的界定理

定理一：


定理二：函数的阶之间的关系具有传递性
定理三：算法的时间复杂度是各步操作时间之和，在常数步的情况下取最高阶的函数即可

1.4.3 一些重要结果

对数函数的阶低于幂函数的阶，多项式函数的阶低于指数函数的阶.

1.5 几类重要函数

1.5.1 对数函数

1.5.2 指数函数与阶乘

1.5.3 取整函数

1.5.4 函数排序

1.6 序列求和

1.6.1 序列求和公式

1.6.2 二分检索算法

1.7 递推方程与算法分析

迭代求时间复杂度

1.7.1汉诺塔算法

解 T(n)=2^n-1（迭代算出
迭代法求递推方程

1.7.2 插入排序

迭代法求递推方程

1.7.3 二分归并问题

换元迭代

1.8 递归树

递归树是迭代计算的模型；递归树生成过程与迭代过程一致；递归树上的所有项恰好是迭代之后产生和式中的项；对递归树上的项求和就是迭代后方程的解
即递归树是迭代的图形表述，递归树的生成规则是用右部形成二层子树来不断替换左部。
此处应用：递归树求时间复杂度

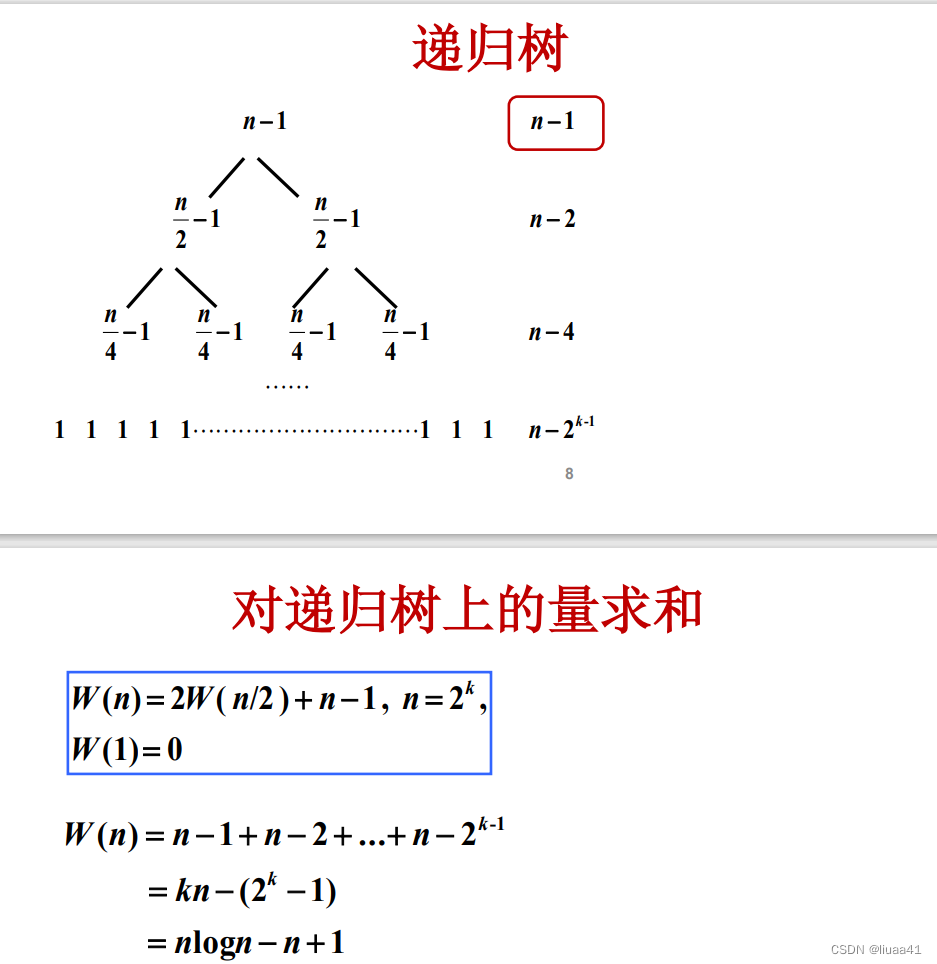
每一层都是n，一共有k层 故时间复杂度是 n*k

1.9 主定理

1.9.1 主定理的应用背景

1.9.2 主定理内容