元:数学上称变量为元
一元统计分析:一个变量(标志值或指标)的统计分析理论和方法(单个随机变量𝑋 )
多元统计分析:主要讲授多变量统计理论和方法(随机向量𝑋=(𝑋1, 𝑋2, … , 𝑋𝑛),𝑋𝑖均为随机变量)
研究内容
1. 简化数据结构(降维问题) ---多变量分析
主成分分析、因子分析、对应分析等多元统计方法:通过变量变换等方法使相互依赖的变量变成互不相关的,或把高维空间的数据投影到低维空间,使问题得到简化而损失的信息又不太多。
2.聚类与判别(归类问题)
聚类分析和判别分析等统计方法:对所考查的对象(样品点或变量)按相似程度进行分类(或归类)
3.变量间的相互联系
分析一个或几个变量的变化是否依赖于另一些变量的变化;如果是,建立变量间的定量关系式,并用于预测或控制---回归分析(两组变量的相依分析);两组变量间的相关分析---偏最小二乘回归分析、典型相关分析等
4.多元统计分析的理论基础
包括多维随机向量及多维正态随机向量,及由此定义的各种多元统计量,推导它们的分布并研究其性质,研究它们的抽样分布理论,这些不仅是统计估计和假设检验的基础,也是多元统计分析的理论基础
5.多元数据的统计推断、基础理论
参数估计和假设检验问题,特别是多元正态分布的均值向量和协差阵的估计和假设检验等问题
变量之间的关系
1.一组变量与单个变量之间的相关关系
回归任务:p个输入变量与单个输出连续型变量之间的关系,如:最小二乘、岭回归、Lasso
分类任务:p个输入变量与单个输出离散型变量之间的关系,如:Fisher线性判别分析
2.一组变量之间的关系
主成分分析:变量转化为若干个少数变量(全部信息)
因子分析:提取变量中共有的潜在内容(公有信息)
概念
多维尺度变换-----已知距离或相似度以图形显示对象间位置信息
对应分析------成对离散型变量的各水平相互关系
聚类分析------依据数据对象间的相似度对其进行分组
分类-----利用已知离散型输出变量的数据建模对预测未来数据输出值
回归-----利用已知连续性输出变量的数据建模对预测未来数据输出值 X→Y
主成分分析-----少数综合变量代替原始变量大部分信息重新表示数据
因子分析-----少数公共因子(潜变量)发掘原始变量共有信息重新表示数据
典型相关分析----寻找两组变量间存在由大到小的典型线性相似度序列
方法
* 多元变量:协方差矩阵、相关系数矩阵、多元正态分布形式
回归分析:最小二乘、Lasso、岭回归、损失函数、可决系数、* 均方误差
* 分类任务:线性投影、极大似然估计
其他任务:聚类及其与分类的区别、主因子、主成分、典型变量
图
基本绘图
import matplotlib.pyplot as plt
import numpy as np
#设置空白画板
fig = plt.figure()
#定义横纵轴关系x、y
x = np.linspace(0, np.pi)
y_sin = np.sin(x)
y_cos = np.cos(x)
y_tan = np.tan(x)
#画板分为2x2网格 4小部分 221、223、224代表所在位置
ax1 = fig.add_subplot(221)
ax2 = fig.add_subplot(223)
ax3 = fig.add_subplot(224)
#画图
ax1.plot(x, y_sin)
ax2.plot(x, y_cos, 'bo-', linewidth=2, markersize=5)
ax3.plot(x, y_tan, color='y', marker='.', linestyle='dashed')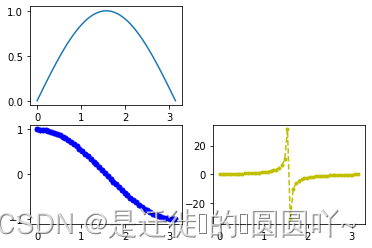
散点图
import matplotlib.pyplot as plt
fig = plt.figure()
x = np.arange(20)
y = np.random.randn(20)
plt.scatter(x, y, color='g', marker='o')
plt.show()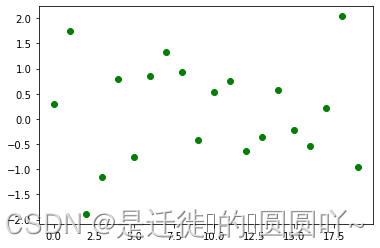
轮廓图
pandas.plotting.parallel_coordinates(frame, class_column)
# frame:DataFrame类型的数据
# class_column:字符串类型,指定哪一列包含类的名字。Column name containing class names.
# 代码实现
pandas.plotting.parallel_coordinates(frame,”序号”)
# 例 1
from pandas.plotting import andrews_curves
import pandas as pd
import matplotlib.pyplot as plt
pd_data=pd.read_csv("ssss.csv")
plt.figure()
parallel_coordinates(pd_data,'Species')
plt.show()
# 例 2
import matplotlib.pyplot as plt
fig = plt.figure()
fig, (ax1, ax2) = plt.subplots(2)
x = np.arange(-8, 7, 0.3)
y = np.arange(-4, 9, 0.1)
xx, yy = np.meshgrid(x, y, sparse=True)
z = np.sin(xx**2 + yy**2) / (xx**2 + yy**2)
ax1.contourf(x, y, z)
ax2.contour(x, y, z)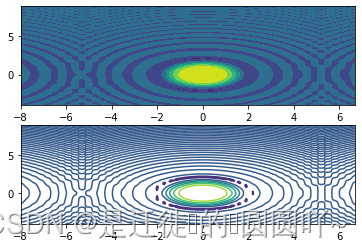
雷达图
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.family']='SimHei'
matplotlib.rcParams['font.sans-serif']=['SimHei']
labels=np.array(['综合','第一周','第二周','第三周','第四周','第五周'])
nAttr=6
Python=np.array([88.7,85,90,95,70,96])
angles=np.linspace(0,2*np.pi,nAttr,endpoint=False)
Python=np.concatenate((Python,[Python[0]]))
angles=np.concatenate((angles,[angles[0]]))
fig=plt.figure(facecolor="white")
plt.subplot(111,polar=True)
plt.plot(angles,Python,'bo-',color='g',linewidth=2)
plt.fill(angles,Python,facecolor='g',alpha=0.2)
plt.thetagrids(angles*180/np.pi,labels)
plt.figtext(0.52,0.95,'python 成绩分析图',ha='center')
plt.grid(True)
plt.savefig('dota_radar.png')
plt.show()
调和曲线图
pandas.plotting.andrews_curves(frame, class_column)
# frame:DataFrame 类型的数据
# class_column:字符串类型,指定哪一列包含类的名字。Column name containing class names.
#例
from pandas.plotting import andrews_curves
import pandas as pd
import matplotlib.pyplot as plt
pd_data=pd.read_csv("xxxx.csv")
plt.figure()
andrews_curves(pd_data,'Species')
plt.show()
散步矩阵图
from pandas.plotting import scatter_matrix
scatter_matrix(frame, alpha=0.5, figsize=None, marker='.')
# frame,pandas dataframe 对象
# alpha, 图像透明度,一般取(0,1]
# figsize,以英寸为单位的图像大小,一般以元组 (width, height) 形式设置marker
# Matplotlib 可用的标记类型,如’.’,’,’,’o’等。
#例
from pandas.plotting import scatter_matrix
import pandas as pd
import matplotlib.pyplot as plt
pd_data=pd.read_csv("yyyy.csv")
plt.figure()
scatter_matrix(pd_data,figsize=(10,10))
plt.show()箱型图
plt.boxplot(x,sym=None,patch_artist=None,showbox=None,showfliers=None, abels=None)
# sym:指定异常点的形状,默认为+号显示;
# patch_artist:是否填充箱体的颜色;
# showbox:是否显示箱线图的箱体,默认显示;
# showfliers:是否显示异常值,默认显示;
# labels:为箱线图添加标签,类似于图例的作用;
#例
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
df =pd.DataFrame(np.random.rand(10,5),columns=['A','B','C','D','E'])
f = df.boxplot(sym = 'o', #异常点形状
vert = True, # 是否垂直
whis=1.5, # IQR
patch_artist = True, # 上下四分位框是否填充
meanline = False,showmeans = True, # 是否有均值线
showbox = True, # 是否显示箱线
showfliers = True, #是否显示异常值
notch = False, # 中间箱体是否缺口
return_type='dict') # 返回类型为字典
plt.title('box')
plt.show()
柱状图
plt.bar(index, values, yerr = std, error_kw = {'ecolor' : '0.2', 'capsize' :6}, alpha=0.7)
# x : 定义柱状图的x轴
# height : 定义柱高
# yerr关键字参数:可传入包含标准差的列表
# error_kw={} , 接收显示误差线的关键字函数
# eColor:指定误差线的颜色
# capsize :指定误差线两头横线的宽度
# alpha:控制彩色条状图的透明度, 范围0-1
import matplotlib.pyplot as plt
import numpy as np
index = np.arange(5)
values = [5, 6, 3, 4, 6]
SD = [0.8, 2, 0.4, 0.9, 1.3]
plt.title('The acc of diffferent algorithms on the same datasets')
plt.bar(index, values, yerr = SD, error_kw = {'ecolor' : '0.2', 'capsize' :6}, alpha=0.7,label = 'classfication accuracy')
plt.xticks(index+0.2,['alg1', 'alg2', 'alg3', 'alg4', 'alg5'])
plt.legend(loc=2)
plt.show()

假设检验
从总体中随机抽取一定含量的样本,用样本指标估计(推断)总体指标:
参数统计:在总体分布类型已知条件下,对未知参数进行检验的方法(样本总体为相互独立的随机样本、正态分布、各总体方差要齐:t检验、F检验)
非参数统计:用符号或等级排列(秩排列)代替数据本身的分析方法(适用于任何分布类型资料的统计分析、秩和检验就是此方法总体分布为偏态或分布未知的计量资料、等级资料、个别数据偏大或小,一端或两端是不确定数值的资料、各组离散程度相差悬殊,即各总体方差不齐)
比较:
| 参数检验 | 非参数检验 |
| 某种分布的总体或总体符合某种假设 | 不拘泥于分布 |
| 对总体参数进行的假设检验 | 在总体方差未知或知道甚少的情况下 利用样本数据对总体分布形态等进行推断的方法 |
| 总体均数或方差 | 不满足参数检验条件时,非参数检验效能体现得好 |
| 如:u检验,t检验,方差分析 | 若满足参数检验条件,尽量应用参数检验,否则影响检验效能 |
方法
Wilcoxon秩和检验(秩检验)
将原始数据从小到大,或等级从弱到强转换成秩后,再对基于秩次的统计量(如秩和)进行检验,做出统计推断
秩号:将各原始数据从小到大排列,分别给每个数据一个顺序号
秩和:用秩次代替原始数据,计算各组秩次之和
秩和检验:基于秩和提供的信息,对不同总体的平均水平进行假设检验
计算过程:
1. 建立检验假设并确定检验水准 :差值的总体中位数
=0,
:
≠0
2. 计算检验统计量
①求各对测量值的差值
②编秩:按照差值的绝对值从小到大编秩。(差值为0者不参加编秩;绝对值相等,符号相同时顺次编秩;绝对值相等,符号相反时取平均秩次)
3. 求秩和、确定检验统计量 T 值:分别求出正秩和、负秩和
4. 确定P 值、作出统计推断结论
检验P值:由检验统计量的样本观察值得出的原 件假设可能被拒绝的最小显著性水平
判定标准:
| P值 | 碰巧的概率 | 对无效假设 |
| P>0.05 | 碰巧出现的可能性大于5% →无显著差异 | 不能否定原假设 |
| P<0.05 | 碰巧出现的可能性小于5%→显著性差异→依据中位数值大小判定 | 可以否定原假设 |
import scipy.stats as stats
stats.wilcoxon( x, y, correction = Flase,alternative = 'two-sided' )
#x:第一组测量值(此情况下,y是第二组测量值)或在两组测量值之间的差(此情况下不指定y)必须是一维的
#y:第二组测量值(若x是第一组测量值)或未指定(若x是两组测量值之间的差)必须是一维的
#correction:如果为True,则是在小样本情况下,在计算Z统计量时用0.5来连续性校正。默认值为False。
#alternative:等于 “two-sided” 或 “greater” 或 “less”
# “two-sided” 为双边检验
# “greater” 为备择假设是大于的单边检验
# “less” 为备择假设是小于的单边检验
#例:
import scipy.stats as stats
x=[310,350,370,377,389,400,415,425,440,295,325,296,250,340,298,365,375,360,385]
y=[320]*len(x)
print(stats.wilcoxon(x,y,correction=True,alternative='greater'))
#out
#WilcoxonResult(statistic=158.0, pvalue=0.004726409912109375)
Mann-Whitney 秩和检验
Wilcoxon 统计量与 Mann-Whitney 统计量是等价的
Wilcoxon 秩和检验主要针对两样本量相同的情况,而 Mann-Whitney 秩和检验考虑到了不等样本的情况,是对 Wilcoxon 秩和检验这一方法的补充
import scipy.stats as stats
scipy.stats.mannwhitneyu( x, y, use_continuity = True, alternative = None )
# x, y:array_like样本数据数组
# use_continuity:bool, optional是否需要0.5的连续性校正,建议小样本需要。默认值为 True
#alternative:{None, ‘less’, ‘two-sided’, ‘greater’}
# ‘two-sided’ 表示双侧检验
# ‘greater’ 为备择假设是大于的单边检验
# ‘less’ 为备择假设是小于的单边检验
# None 表示双侧检验 p 值的一半,默认值为 None
# 例
import scipy.stats as stats
weight_high=[134,146,104,119,124,161,107,83,113,129,97,123]
weight_low=[70,118,101,85,112,132,94]
stats.mannwhitneyu(weight_high,weight_low,alternative='two-sided')
# out
#MannwhitneyuResult(statistic=62.0, pvalue=0.10026196713503215)Friedman Test
在一组数据集上对多个算法进行比较,能够充分利用相关样本中的全部信息
目的是确定中位数之间的任何差值在统计意义上是否显著
from scipy.stats import friedmanchisquare
scipy.stats.friedmanchisquare(measurements1, measurements2, measurements3…)
# 参数:
# measurements1, measurements2, measurements3... : array_like
# 试验数据样本,每组样本量相等,且输入的顺序不能打乱,至少需要三组试验数据
# 返回:
# friedman 卡方统计量: float类型,the test statistic, correcting for ties
# p-value : float,
# the associated p-value assuming that the test statistic has a chi squared distribution
# 例
from numpy.random import seed
from numpy.random import randn
from scipy.stats import friedmanchisquare
# seed the random number generator
seed(1)
# generate three independent samples
data1 = 5 * randn(100) + 50
data2 = 5 * randn(100) + 50
data3 = 5 * randn(100) + 52
stat, p = friedmanchisquare(data1, data2, data3)
print('Statistics=%.3f, p=%.3f' % (stat, p))
alpha = 0.05
if p > alpha:
print('Same distributions (fail to reject H0)')
else:
print('Different distributions (reject H0)')
# out
# Statistics=9.360, p=0.009
# Different distributions (reject H0)
检验图: 
横轴是平均序值,对每个算法用一个圆点显示其平均序值,以圆点为中心的横线段表示临界值域的大小 然后就可从图中观察,若两个算法的横线段有交叠,则说明这两个算法没有显著差别,否则即说明有显著差别
主成分分析
降维思想:用较少的变量来代替原来较多的变量(全部信息)
降维可能性:数据的特征或信息是由各个变量描述的,在不同数据中的变量之间关系也不同
数据各变量不相关的情况:若一个数据的变量互相独立或不相关,则每个变量对于此数据的整体特征的贡献都是独立的, 降维没有意义
数据各变量相关的情况:由于变量之间相关,就有降维的可能
主成分分析思想:在数据各变量相关的情况下,将原始变量做线性加权形成若少数几个线性无关的综合变量,并反映出原变量的大部分信息。当第一个线性组合不能提取更多的信息时,再考虑用第二个线性组合继续这个快速提取的过程,……,直到所提取的信息与原指标相差不多时为止,这些线性组合称为主成分
基本步骤:先找出所有主成分然后再根据主成分信息量的大小筛选出少数主成分
1.寻找p个线性无关的综合变量(即主成分), 满足各成分反映原始变量信息是递减的,information(𝑍𝑖)≥ information(𝑍𝑖+1) 且𝑍𝑖与𝑍𝑗(𝑖 ≠ 𝑗)是线性无关的
2.依据各主成分的反映原始变量信息量的大小,确定哪几个主成分可以反映原始变量的大部分信息
3.利用选择出的主成分(综合变量𝑍1, 𝑍2, . . 𝑍𝑝) 重新表示原始数据
第一主成分

第二主成分

第一主成分就是求协方差矩阵Σ的最大特征值对应的单位特征向量
sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)
# n_components : int, float, None or string。降维后的主成成分数量
# 若0 < n_components < 1,则方差和需大于n_components所指定的阈值,PCA会自动选择下降维数
# 如果n_components取整数,则事先指定主成分个数
# copy:True 或 False,默认为True,即是否需要将原始训练数据复制
# whiten:True 或 False,默认为False,即是否白化,使得每个特征具有相同的方差
# 例1
import pandas as pd
import numpy as np
import sklearn.decomposition as dp
w=pd.read_csv("aaup.csv")
u=w[w.columns[4:]]
data =np.array(u)
pca=dp.PCA(n_components=0.90)
pca.fit(data)
reduce_data = pca.transform(data)
reduced_x=pca.fit_transform(data) #压缩后的数据
reduced_x1= np.dot(data,pca.components_.T)
print(pca.components_)#各主成分的权向量
# pca.n_components # 在此临界值下筛选出主成分个数
# print(pca.n_component)#不大行
#例2
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import sklearn.decomposition as dp
w = pd.read_csv('AAUP.csv')
u = w[w.columns[4:]]
X = np.array(u)
pca = dp.PCA(n_components=2)
Y = pca.fit_transform(X) #主成分得分
print(pca.explained_variance_ratio_) #方差百分比
plt.figure(figsize = (10,7))
plt.scatter(pca.components_[0],pca.components_[1])
for i in range(13):
plt.text(pca.components_[0,i],pca.components_[1,i],w.columns[4:][i],fontsize=20)
plt.title("loadings")
plt.xlabel("Component 1")
plt.ylabel("Component 2")
plt.grid(True)
plt.show()
主要方法
1.fit(X): 用数据X来训练PCA模型
2. transform(X):将数据X转换成降维后的数据,模型训练好后,对于新输入的数据也可以用transform方法来降维
3. fit_transform(X):用X来训练PCA模型,同时返回降维后的数据 (1.+2.=3.)
4. inverse_transform(newData) :将降维后的数据换成原始数据,可能不会完全一样,会有差别
PCA缺陷
1.若对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高
2.特征值分解有一些局限性,比如变换的矩阵必须是方阵
3.在非高斯分布情况下,PCA方法得出的主成分可能并不是最优的
4.主成分物理意义解释困难
因子分析
定义:研究从变量群中提取共性因子的统计技术,即将相同本质的变量归入一个因子,可减少变量的数目,还可检验变量间关系的假设(公有信息)
主要应用
1.寻求基本结构,简化观测系统,将具有错综复杂关系的对象(变量或样品)综合为少数几个因子(不可观测的,相互独立的随机变量),以再现因子与原变量之间的内在联系,如:挑选参加十项全能的运动员健将,只需要寻找满足短跑速度、爆发性、臂力、腿力、耐力五个指标即可
2.用于分类,对p个变量或n个样品进行分类
类型
根据研究对象可分为R型和Q型因子分析:
1.R型因子分析:研究变量(指标)之间的相关关系,通过对变量的相关阵或协差阵内部结构的研究找出控制所有变量的几个公共因子 (或称主因子、潜因子),用以对变量或样品进行分类
2.Q型因子分析:研究样品之间的相关关系,通过对样品的相似矩阵内部结构的研究找出控制所有样品的几个主要因素(或称主因子)
因子分析与主成分分析的区别
| 主成分分析 | 因子分析 |
| 一般不用数学模型来描述,只是通常的变量变换 | 需要构造因子模型(正交或斜交) |
| 主成分的个数和变量个数p相同,将一组有相关性的变量变换为一组独立的综合变量(一般只选取m(m<p)个主成分 | 用尽可能少的公因子构造一个结构简单的因子模型 |
| 将主成分表示为原变量的线性组合 | 将原始变量表示为公因子和特殊因子的线性组合 |
| 尽量包含原始变量的全部信息 | 尽量包含原始变量的公有信息 |
因子模型

称为X的公共因子,对X每一个分量
都有作用
称为X的特殊因子,只对
起作用
各特殊因子之间以及特殊因子与所有公共因子之间都是相互独立的
模型不受单位影响
常用参数估计方法
1.主因子法
2.主成分法
3.极大似然法
因子旋转
求出公共因子,知道每个公共因子的实际意义,对实际问题作出科学的分析:若载荷矩阵A的所有元素都接近0或±1,则模型的公共因子就易于解释;若载荷矩阵A的元素多数居中,不大不小,则对模型的公共因子往往就不易作出解释,此时应考虑进行因子旋转,使得旋转之后的载荷矩阵在每一列上元素的绝对值尽量地拉开大小距离
因子得分
性质
评价每个样本在每个公共因子上的分值,该分值包含了原始变量的信息,可用于代替原始变量进行其他统计分析,比如回归分析,可以考虑将因子得分作为自变量,与对应的因变量进行回归
原始变量的数值是可以直接观测到的,而因子得分只能通过原始变量和因子之间的关系计算得到,且因子得分是经过标准化之后的数值, 各个因子得分之间不受量纲的影响
应用

from sklearn.decomposition import FactorAnalysis
fa = FactorAnalyzer(n_factors=3, rotation='promax', method='minres’)
# n_factors: int,主因子的个数
# rotation: str类型, 因子旋转方法: 方差旋转方法
# 'varimax' (方差最大正交旋转)
# ' promax'(方差最大斜交旋转)
# 'None'(不做旋转)
# method: str类型, 因子求解法,'minres'(主因子法), 'ml'(极大似然估计), ‘principal’(主成分法)
# 例
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import FactorAnalysis
from sklearn import preprocessing
w = pd.read_csv('AAUP.csv')
u = w[w.columns[4:]]
u_scale = preprocessing.scale(u)
fa = FactorAnalysis(tol = 1e-8,max_iter = 10000)
fa.n_components = 2
fa.fit(np.array(u_scale))
fa.components_
print(pd.DataFrame(fa.components_,columns = u.columns))
CA = np.array(w[w.columns[2]]=='CA')
name_CA = np.array(w[w.columns[1]][CA])
sc1 = fa.fit_transform(u_scale)[CA,:]
fig = plt.figure(figsize=(10,8))
fig.add_subplot(121)
plt.scatter(fa.components_[0],fa.components_[1])
for i in range(len(u.columns)):
plt.text(fa.components_[0,i],fa.components_[1,i],u.columns[i])
plt.grid(True)
plt.title("Loadings")
plt.xlabel("Factor 1")
plt.ylabel("Factor 2")
plt.show()
主要方法
拟合数据:fa.fit(X) 与Sklern类似 X:array-like
因子共同度:fit .get_communalities(),返回所有因子对各变量的贡献度array
因子载荷:fa.loadings_,返回载荷矩阵
因子方差信息:fa.get_factor_variance(), 返回各因子方差、方差矩阵比例和累计方差矩阵
因子特征值:fa. get_eigenvalues(), 普通返回原始特征值和公因子特征值
因子得分:fa.transform(X) ,返回每条数据的公因子表示形式
典型相关分析
概述:研究两组变量之间相关关系的一种多元统计方法,能够揭示出两组变量之间的内在联系
目的:识别并量化两组变量之间的联系,将两组变量相关关系的分析转化为一组变量的线性组合与另一组变量线性组合之间的相关关系分析
基本思想:
1.在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数
2.选取和最初挑选的线性组合不相关的线性组合使其配对,选取相关系数最大的一对
3.如此继续下去,直到两组变量之间的相关性被提取完毕
被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数,典型相关系数度量了这两组变量之间联系的强度
总体典型相关
第一典型变量性质与相关概念

第二典型变量性质



样本典型相关
实际应用中,总体的协方差矩阵常常是未知的,类似于其他的统计分析方法, 需要从总体中抽出一个样本,根据样本对总体的协方差或相关系数矩阵进行估计, 然后利用估计得到的协方差或相关系数矩阵进行分析。
样本协方差矩阵受量纲变化影响较大,需要利用标准化处理后再计算协方差矩阵
计算步骤步骤: 数据标准化 → 计算协方差矩阵 → 求解构造矩阵特征值及其对应的特征向量
from sklearn.cross_decomposition import CCA
cca=CCA(n_components=2, scale=True)
# n_components:综合变量的个数 , [1, min(n_samples, n_features, n_targets)]
# scale=True:是否对变量进行归一化处理
# 例
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import CCA
w=pd.read_csv("full.aaup.csv程序")
u=w[w.columns[4:]]
X=np.array(u[u.columns[:8]])
Y=np.array(u[u.columns[8:]])
cc=CCA(3)
cc.fit(X,Y)
X_c, Y_c = cc.transform(X, Y)
print (cc.x_weights_)
print (cc.y_weights_)
print (cc.x_loadings_)
print (cc.y_loadings_)
print (cc.x_scores_)
print (cc.y_scores_)
# out
# [[ 0.13888949] [ 0.0210999 ] [ 0.05452574] [-0.22438768] [ 0.79153085] [ 0.40780574] [ 0.36064397][ 0.063647 ]]
# [[1.]]
# [[0.36389894] [0.31334059][0.34390986] [0.35999676] [0.63338528] [0.63257995 [0.62499499] [0.31673633]]
# [[1.]]
# [[-1.07954684] [ 0.56536426][-0.90576442] ... [-0.88798116] [-0.90159867] [ 1.60485558]]
# [[-0.7174755 ] [ 0.46689629] [-0.59649128] ... [-0.5837561 ] [-0.61241026] [1.06226597]]方法:X_c,Y_c = cca.fit_transform(X[, Y, copy]): 应用维数约简至X_c,Y_c
属性: x_weights_, y_weights_:典型变量的权重
x_loadings_, y_loadings_:典型变量的载荷
x_scores_, y_scores_:典型变量的得分
聚类分析(群分析)
研究依据样本或指标进行“分类” 的一种多元统计方法(类:相似元素的集合)
聚类:事先不知道研究的问题应分几类,不知道观测到的个体的具体分类情况
目的:通过对观测数据所进行的分析处理,选定一种度量个体接近相似程度的统计量确定分类数据,建立一种归类方法,并按接近程度对观测对象给出对象合理的分类
判别分析与聚类分析的区别
两者所起作用不同
判别分析方法假定组(或类)已事先分好,判别新样本应归属哪 一组,对组的事先划分有时也可以通过聚类分析得到
聚类分析方法是事先不知对象分几类的情况下,依据对象间相似程度将其分成若干类,相似的归为同一类,不相似的归为不同的类
监督学习和无监督学习
监督学习:给定的数据集中每个输入数据均有一个输出数据(标签,label),利用输入和输出数据进行建模,并对未有输出的输入数据预测其输出
无监督学习:给定的数据集中每个输入数据没有输出(或结果),仅利用当前的输入数据发现数据内部的结构或性质
变量类型

主要聚类方法
方法区别在于类与类之间距离计算方法不同
层次聚类法
将n个样本各自作为一类,并规定样本之间的距离和类与类之间的距离,然后将距离最近的两类合并成一个新类,计算新类与其他类的距离;重复进行两个最近类的合并,每次减少一类,直至所有的样本合并为一类
优缺点
| 优点 | 缺点 |
| 相似度容易定义,限制少 | 计算复杂度太高 |
| 不需要预先指定聚类数 | 受奇异值影响较大 |
| 不需要预先指定聚类数 | 算法很可能聚类成链状 |
| 可以聚类成其它形状 |
系统聚类的基本步骤

# 1. sklearn实现
from sklearn.cluster import AgglomerativeClustering
AgglomerativeClustering(n_clusters=2, affinity=’euclidean, linkage=’ward’)
# n_clusters:一个整数,指定分类簇的数量
# affinity:距离度量。取值为:’euclidean’,’l1’,’l2’,’mantattan’,’cosine’,’precomputed’,
# 如果linkage=’ward’,则affinity必须为’euclidean’
# linkage衡量簇与簇之间的远近程度的方法
# 主要有:‘ward’:最小距离, ‘complete’:最大距离,‘average’:平均距离
# 例
from sklearn.cluster import AgglomerativeClustering
import numpy as np
X = [[1,2],[3,2],[4,4],[1,2],[1,3]]#生成数据
clustering = AgglomerativeClustering().fit(X)#训练模型
clustering.labels_
clustering.children_属性:labels:每个样本的簇标记
n_leaves_:层次树的叶节点数量
n_components:连接图中连通分量的估计值
children:一个数组,给出了每个非节点数量
方法:fit(X[,y]):训练样本
fit_predict(X[,y]):预测每个样本的簇标记
# 2.Scipy实现
from scipy.cluster.hierarchy import dendrogram, linkage,fcluster
z=linkage(y, method=’single’, metric=’euclidean’) #聚类结果
# y:数据矩阵
# method:衡量簇与簇之间的远近程度的方法
# 主要有‘single:’:最小距离,‘complete’:最大距离,‘average’:平均距离
# Metric距离度量:,’l1’,’l2’,’mantattan’,’cosine’,’precomputed’等
fcluster(z, t=k, criterion=‘maxclust’) #定义小类聚集准则
# Z代表Z是linkage得到的矩阵,记录了层次聚类的层次信息
# t为类的个数, criterion='maxclust‘or ‘maxclust_monocrit’
# t为阈值, criterion= ‘inconsistent’, ‘distance’ or ‘monocrit’
dendrogram(Z) #制作谱系图
#例
from scipy.cluster.hierarchy import dendrogram, linkage,fcluster
from matplotlib import pyplot as plt
X = [[1,2],[3,2],[4,4],[1,2],[1,3]]
Z = linkage(X, 'ward')
f = fcluster(Z,4,'distance')
fig = plt.figure(figsize=(5, 3))
dn = dendrogram(Z)
plt.show()



动态聚类法
选择一批凝聚点或给出一个初始的分类, 让样本按某种原则向凝聚点凝聚,对凝聚点进行不断的修改或迭代, 直至分类比较合理或迭代稳定为止。类的个数k可以事先指定,也可以在聚类过程中确定。
选择初始凝聚点(或给出初始分类)的一种简单方法是采用随机抽选(或随机分割)样本的方法
k均值法基本步骤
(1)选择k个样本作为初始凝聚点,或者将所有样本分成k个初始类,然后将这k个类的重心(均值)作为初始凝聚点
(2)对除凝聚点之外的所有样本逐个归类,将每个样本归入凝聚点离它最近的那个类(通常采用欧氏距离),该类的凝聚点更新为这一类目前的均值,直至所有样本都归了类
(3)重复步骤(2),直至所有的样本都不能再分配为止
最终的聚类结果在一定程度上依赖于初始凝聚点或初始分类的选择。经验表明,聚类过程中的绝大多数重要变化均发生在第一次再分配中
有序样本聚类法
模糊聚类法
聚类预报法
类间距离(联系准则)方法
在分层抽样中需要应用类间距离的概念,由一个点组成的类是最基本的类。如果每一类都由一个点组成,那么点间的距离就是类间距离
最短距离法:不适用于分离得很差的群体
最长距离法:受异常值影响较大
中间距离法:仅利用部分样本的信息
类平均法:利用了所有样本之间的信息,计算复杂度高
重心法:对异常值鲁棒,效果不如类平均法
离差平方和法(Ward方法):大类分隔,小类合并
最短距离法、最长距离法、可变法、类平均法、可变类平均法、离差平方和法都具有单调性
中间距离法和重心法不具有单调性
距离公式
明考夫斯基(Minkowski)距离:
q=1:绝对值距离(曼哈顿距离、城市街区距离)
q=2:欧氏距离
q=∞:切比雪夫距离
兰氏(Lance和Williams)距离
马氏(Mahalanobis)距离
斜交空间距离
霍普金斯统计量
import pandas as pd
from numpy.random import uniform,normal
from scipy.spatial.distance import cdist
#霍普金斯统计量计算,input:DataFrame类型的二维数据,output:float类型的霍普金斯统计量
#默认从数据集中抽样的比例为0.3
def hopkins_statistic(data:pd.DataFrame,sampling_ratio:float = 0.3) -> float:
#抽样比例超过0.1到0.5区间任意一端则用端点值代替
sampling_ratio = min(max(sampling_ratio,0.1),0.5)
n_samples = int(data.shape[0] * sampling_ratio)
sample_data = data.sample(n_samples)
#原始数据抽样后剩余的数据
data = data.drop(index = sample_data.index) #,inplace = True)
#原始数据中抽取的样本与最近邻的距离之和
data_dist = cdist(data,sample_data).min(axis = 0).sum()
#人工生成的样本点,从平均分布中抽样(artificial generate samples)
ags_data = pd.DataFrame({col:uniform(data[col].min(),data[col].max(),n_samples)for col in data})
#人工样本与最近邻的距离之和
ags_dist = cdist(data,ags_data).min(axis = 0).sum()
#计算霍普金斯统计量H
H_value = ags_dist / (data_dist + ags_dist)
return H_value
#实现
#生成符合均匀分布的数据集
data = pd.DataFrame(uniform(0,10,(50000,10)))
print(hopkins_statistic(data))
#生成符合正态分布的数据集
data = pd.DataFrame(normal(size = (50000,10)))
print(hopkins_statistic(data))
#生成由两个不同的正态分布组成的数据集
data = pd.DataFrame(normal(loc = 6,size = (25000,10))).append(pd.DataFrame(normal(size = (25000,10))),ignore_index = True)
print(hopkins_statistic(data))
#out
# 0.5002200786768
# 0.76666522977265
# 0.8811872739163399
判别分析
分类:利用已知类别的数据进行建模,并利用该模型预测未知类别数据属于已知类别的哪一类,所有变量都起作用
聚类:对无类别的数据进行建模,依据数据之间特征的相似性进行分组,只有和因变量各类特点有关的变量起作用
聚类和分类方法没有必然联系,聚类要求数据的非均匀分布
当因变量是数量变量时,称为回归;而当因变量是分类变量(定性变量)时,称为分类
经典统计中,分类被称为判别分析
判别分析的基本思想
在已知研究对象分为若干类型(类别)并已经取得各种类型的一批已知样品的观测数据基础上,根据某些准则,建立起尽可能把属于不同类型的数据区分开来的判别函数,然后用它们来判别未知类型的样品应该属于哪一类
主要问题是如何寻找最佳的判别函数和建立判别规则
Fisher判别分析(降维)
利用投影使多维问题简化为一维问题来处理,选择一个适当的投影轴,使所有的样本点都投影到这个轴上得到一个投影值,使每一类内的投影值所形成的类内离差尽可能小,而不同类间的投影值所形成的类间离差尽可能大
from sklearn import discriminant_analysis as da
da.LinearDiscriminantAnalysis(solver='svd', shrinkage=None, priors=None, n_components=None)
# solver:逆矩阵求解方式,‘svd‘(默认), ’lsqr‘, ’eigen‘(数据稀疏时使用)
# Shrinkage:收缩系数,当数据稀疏时配合’lsqr‘, ’eigen‘使用:’auto‘(使用Ledoit-Wolf引理);
#float, between 0 and 1
# n_components:投影后数据的维数,默认min(n_classes - 1, n_features)
#例
from sklearn import datasets,discriminant_analysis
from sklearn.model_selection import train_test_split
iris=datasets.load_iris()
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target,train_size=0.8,stratify=iris.target)
lda=discriminant_analysis.LinearDiscriminantAnalysis()
lda.fit(x_train,y_train)
print('Coefficients:%s, intercept %s'%(lda.coef_,lda.intercept_))#输出权重向量和b
print('Score: %.2f' % lda.score(x_test, y_test))#测试集
print('Score: %.2f' % lda.score(x_train, y_train))#训练集
#out
# Coefficients:[[ 6.07407772 11.43815437 -16.09169122 -20.14736836]
# [ -1.79795467 -4.30399243 4.36082508 3.43914366]
# [ -4.27612305 -7.13416194 11.73086615 16.7082247 ]], intercept [-14.7074152
# 0.19664648 -34.450291 ]
# Score: 1.00
# Score: 0.97属性:coef_:权向量
intercept_:偏置
explained_variance_ratio:_可解释方差比例
方法:fit(X, y):训练模型predict(X):预测模型
score(X, y):模型精度
Logistic回归模型
所有参数可以用最大似然法解出
from sklearn.linear_model import LogisticRegression
model =LogisticRegression(penalty='l2', *, dual=False, solver='lbfgs', multi_class='auto')
# penalty:字符串型,正则化类型, 'l1' or 'l2',默认:'l2’
# dual:布尔型,默认:False。当样本数>特征数时,令dual=False;用于liblinear解决器中L2正则化
# multi_class:字符串型,{ovr', 'multinomial'},默认:'ovr';如果选择的选项是“ovr”,
# 那么一个二进制问题适合于每个标签,否则损失最小化就是整个概率分布的多项式损失
# 对liblinear solver无效
# solver:{'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'},默认: 'liblinear'
#例
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
X, y = load_iris(return_X_y=True)#导入自带数据集
clf = LogisticRegression(random_state=0).fit(X, y)# 建模
print(clf.predict(X[:2, :])) #预测类别
print(clf.predict_proba(X[:2, :])) #预测数据属于各类的概率
print(clf.score(X, y)) #模型分类精度
#out
# [0 0]
# [[9.81814805e-01 1.81851810e-02 1.43953228e-08]
# [9.71754998e-01 2.82449715e-02 3.01061907e-08]]
# 0.9733333333333334方法:fit(X, y[, sample_weight]):利用当前数据训练模
predict(X):当前数据的预测输出类别
predict_proba(X):返回X中归属所有类的预测概率
score(X, y[, sample_weight]):返回测试分类精度
优势:
(1)几率函数任意阶可导,有很好的数学性质,许多现有的数值优化算法都可用来求最优解,训练速度快
(2)简单易理解,模型可解释性非常好,从特征的权重可以看到不同的特征对最后结果的影响
(3)适合二分类问题,不需要缩放输入特征
(4)内存资源占用小,因为只需要存储各个维度的特征值
(5)直接对分类可能性进行建模,无需事先假设数据分布,避免了假设分布不准确所带来的问题
(6)以概率的形式输出,而非知识0-1判定,对许多利用概率辅助决策的任务很有用
不足:
(1)不能用逻辑回归去解决非线性问题,因为Logistic的决策面是线性的
(2)对多重共线性数据较为敏感
(3)很难处理数据不平衡的问题
(4)准确率并不是很高,形式非常的简单(非常类似线性模型),很难拟合数据的真实分布
(5)逻辑回归本身无法筛选特征,有时会用gbdt来筛选特征,然后再上逻辑回归
回归分析
回归分析用于确定一个或几个连续变量(称为响应变量、因变量或指标)与另一些连续变量(称为自变量或因素)间的相互依赖关系
如果只要考察某一个因变量与其余多个变量的相互依赖关系,称之为多元回归问题
如果要同时考察p个因变量与m个自变量的相互依赖关系,称之为多因变量的多元回归问题(简称为多对多回归)
损失函数

模型预测性能
利用当前数据建立的模型可能适用于这部分数据,但难以保证对其他数据仍然有效,必须由未参加建模的数据来验证
将数据集分为三部分:训练集、验证集、测试集。训练集用于训练数据,验证集用于模型的选择,测试集用于最终的对学习方法的评估
Sklearn-线性回归分析

最小二乘API

最小二乘法缺陷
当样本矩阵X不是列满秩时,或者某些列之间的线性相关性比较大时,行列式接近于0,即接近于奇异。此时计算时误差会很大,传统的最小二乘法缺乏稳定性与可靠性。
训练集与测试集的划分
from sklearn.model_selection import train_test_split
X_train,X_test, y_train, y_test = train_test_split(X,Y, test_size=None, train_size=None, random_state=None, shuffle=True, stratify=None)
# X:待划分的样本特征集合(array-like)
# Y: 待划分的样本标签(array-like)
# test_size:若在0~1之间,为测试集样本数目与原始样本数目之比,若为整数,则是测试集样本的数目
# random_state:随机数种子输出参数: X_train:划分出的训练集数据
X_test:划分出的测试集数据
y_train:划分出的训练集标签
y_test:划分出的测试集标签
交叉验证:简单交叉验证(holdout)、k折交叉验证、留一法
K折交叉验证
①将已知数据随机的切分成K个互不相交、大小相同的子集
②利用K-1个子集的数据训练模型,余下的子集测试模型
③将②过程对所有的K种选择重复进行
④选出K次评测中平均测试误差最小的模型
# K折交叉验证模型实现方式
from sklearn.model_selection import cross_val_score
cross_val_score(estimator, X, y=None, groups=None, scoring=None, cv=None)
# estimator:就是自己选定的模型
# X:array类型数据。训练集的自变量部分
# y:array类型数据。训练集的因变量部分
# cv:int类型。设定cross-validation的维度
# 不设定cv:使用默认值3,即k-fold=3
# 用作交叉验证迭代器的对象
#K折交叉验证数据实现方式
from sklearn.model_selection import Kfold, StratifiedKFold
kfolds = KFold(n_splits=5, shuffle=False, random_state=None)
# n_splits :折的数量
# shuffle :是否打乱顺序
# random_state:随机数种子
方法:Kfolds.split(X,y): 对数据集X进行切分
输入:数据array的X,y
输出:返回测试集与训练集的K个组合的索引值
import numpy as np
from sklearn.model_selection import StratifiedKFold
X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
y = np.array([0, 0, 1, 1])
skf = StratifiedKFold(n_splits=2)
for train_index, test_index in skf.split(X, y):
print("TRAIN:", train_index, "TEST:", test_index)
#out
# TRAIN: [1 3] TEST: [0 2]
# TRAIN: [0 2] TEST: [1 3]岭回归
专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于最小二乘法
Lasso回归
通过构造一个惩罚函数得到一个较为精炼的模型,使得它压缩一些回归系数,即强制系数绝对值之和小于某个固定值,促使一些回归系数为零,因此保留子集收缩的优点, 是一种处理具有复共线性数据的有偏估计
可决系数
为避免量纲带来绝对差异问题而引入,可决系数取值越大,模型拟合度越高。
对应分析
成对离散型变量的各水平相互关系
利用“降维”的方法,以两变量的交叉列联表为研究对象,通过图形的方式,直接揭示变量之间以及变量的不同水平之间的联系,特别适合于多水平离散型变量研究的一种多元统计分析方法
若某两个数据点相距较近,则表明行变量的相应两个水平在列变量所有水平上的频数分布差异均不明显
基本思想
1.编制两离散型变量的交叉列联表,将交叉列联表中的每个数据单元看成两变量在相应水平上的对应点
2.对应分析将变量及变量之间的联系同时反映在一张二维或三维的散点图上,并使联系密切的水平点较集中,联系疏远的水平点较分散
3.通过观察对应分布图就能直观地把握变量水平之间的联系
优点
定性变量划分的类别越多,这种方法的优越性越明显
揭示行变量类间与列变量类间的联系
将类别的联系直观地表现在图形中
缺点
不能用于相关关系的假设检验
维数有研究者自定
受极端值的影响






















 1585
1585











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








