我们使用lingo可以解决数学规划问题,网络优化,多目标规划,博弈论,排队论,决策分析以及最小二常法等问题,而且编程简单易懂,是我们进行建模开发的必备技能之一。
1.Lingo中关系运算符
在LINGO中,关系运算符主要是被用在模型中,来指定一个表达式的左边是否等于、小于等于、或者大于等于右边,形成模型的一个约束条件。关系运算符与逻辑运算符截然不同,前者是模型中该关系运算符所指定关系的为真描述,而后者仅仅判断一个该关系是否被满足:满足为真,不满足为假。
LINGO有三种关系运算符:“=”、“<=”和“>=”。LINGO中还能用“<”表示小于等于关系,“>”表示大于等于关系。LINGO 并不支持严格小于和严格大于关系运算符。
2.数学函数
LINGO提供了大量的标准数学函数,具体如下表所示:
| 数学函数 | 意义 |
|---|---|
| @abs(x) | 返回x 的绝对值 |
| @sqrt() | 开方 |
| @sin(x) | 返回x 的正弦值,x 采用弧度制 |
| @cos(x) | 返回x 的余弦值 |
| @tan(x) | 返回x 的正切值 |
| @exp(x) | 返回常数e 的x 次方 |
| @log(x) | 返回x 的自然对数 |
| @lgm(x) | 返回x 的gamma 函数的自然对数 |
| @sign(x) | 如果x<0 返回-1;否则,返回1 |
| @floor(x) | 返回x的整数部分。当x>=0 时,返回不超过x 的最大整数;当x<0时,返回不低于x 的最大整数。 |
| @smax(x1,x2,…,xn) | 返回x1,x2,…,xn 中的最大值 |
| @smin(x1,x2,…,xn) | 返回x1,x2,…,xn 中的最小值 |
3.变量界定函数
变量界定函数实现对变量取值范围的附加限制,共4种
@bin(x) 限制x 为0 或1 — 用于0-1规划
@bnd(L,x,U) 限制L≤x≤U
@free(x) 取消对变量x 的默认下界为0 的限制,即x 可以取任意实数
@gin(x) 限制x 为整数
在默认情况下,LINGO 规定变量是非负的,也就是说下界为0,上界为+∞。@free 取消了默认的下界为0的限制,使变量也可以取负值。@bnd用于设定一个变量的上下界,它也可 以取消默认下界为0的约束。
4.sum函数与for函数
1.sum函数
使用语法:
@sum(集合(下标):集合表达式);
代码示例:
| 表达方式 | 示例 |
|---|---|
| 数学表达式 | m i n = ∑ i = 1 3 ∑ j = 1 3 x ( i ) ∗ d ( i , j ) min=\sum_{i=1}^{3}\sum_{j=1}^{3}x(i)*d(i,j) min=∑i=13∑j=13x(i)∗d(i,j) |
| Lingo编码 | m i n = min= min=@ s u m ( a r c ( i , j ) : x ( i ) ∗ d ( i , j ) ) sum(arc(i,j):x(i)*d(i,j)) sum(arc(i,j):x(i)∗d(i,j)) |
arc是一个3*3集合(矩阵)
2.for函数
使用方法:
@for(集合(下标)[逻辑表达式]:集合表达式);
代码示例:
| 表达方式 | 示例 |
|---|---|
| 数学表达式 | x ( i ) < 10 ; i ϵ { 1 , 2 , 3 } x(i)<10;i\epsilon\left \{ 1,2,3 \right \} x(i)<10;iϵ{1,2,3} |
| Lingo编码 | @ f o r ( n o d e ( i ) : x ( i ) < 10 ) for(node(i):x(i)<10) for(node(i):x(i)<10) |
node同样是一个集合(矩阵)
5.常见的线性规划问题

对应求解的lingo程序如下所示:
model:
sets:
row/1..3/:b;
col/1..4/:c,x;
link(row,col):a;
endsets
data:
c=6 2 3 9;
a=5 6 -4 -4 3 -3 2 8 4 2 -1 3;
b=2 25 10;
enddata
max=@sum(col:c*x);
@for(row(i):@sum(col(j):a(i,j)*x(j))<b(i));
end
注意:lingo程序中的变量默认都是非负数。
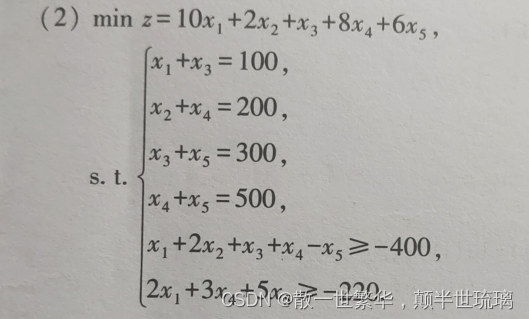
对应的lingo程序如下所示:
model:
sets:
row1/1..4/:b1;
row2/1..2/:b2;
col/1..5/:c,x;
link1(row1,col):a1;
link2(row2,col):a2;
endsets
data:
c=10 2 1 8 6;
a1=1 0 1 0 0 0 1 0 1 0 0 0 1 0 1 0 0 0 1 1;
a2=1 2 1 1 -1 2 0 0 3 5;
b1=100 200 300 500;
b2=-400 -220;
enddata
min=@sum(col:c*x);
@for(row1(i):@sum(col(j):a1(i,j)*x(j))=b1(i));
@for(row2(i):@sum(col(j):a2(i,j)*x(j))>b2(i));
@for(col:@free(x));
end

对应求解的lingo程序如下所示:
model:
sets:
row/1..3/:b;
col/1..5/:c,x,L,U;
link(row,col):a;
endsets
data:
b=20 30 10;
c=8 6 5 9 3;
a=2 9 -1 3 1 1 -3 2 6 1 1 2 -1 1 -2;
L=-10 -50 -15 -20 -30;
U=20,50,60,30,10;
enddata
min=@sum(col:c*x);
@for(row(i):@sum(col(j):a(i,j)*x(j))<=b(i));
@for(col:@bnd(L,x,U));
end


























 6314
6314

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










