SUSCTF_Crypto_large case_复现
k
e
y
w
o
r
d
s
:
keywords:
keywords: e与欧拉函数非互质的RSA解密,恢复e,消除padding,除去部分e的素因子
D e s c r i p t i o n Description Description
from Crypto.Util.number import *
from secret import e,message
def pad(s):
if len(s)<3*L:
s+=bytes(3*L-len(s))
return s
L=128
p=127846753573603084140032502367311687577517286192893830888210505400863747960458410091624928485398237221748639465569360357083610343901195273740653100259873512668015324620239720302434418836556626441491996755736644886234427063508445212117628827393696641594389475794455769831224080974098671804484986257952189021223
q=145855456487495382044171198958191111759614682359121667762539436558951453420409098978730659224765186993202647878416602503196995715156477020462357271957894750950465766809623184979464111968346235929375202282811814079958258215558862385475337911665725569669510022344713444067774094112542265293776098223712339100693
r=165967627827619421909025667485886197280531070386062799707570138462960892786375448755168117226002965841166040777799690060003514218907279202146293715568618421507166624010447447835500614000601643150187327886055136468260391127675012777934049855029499330117864969171026445847229725440665179150874362143944727374907
n=p*q*r
assert isPrime(GCD(e,p-1)) and isPrime(GCD(e,q-1)) and isPrime(GCD(e,r-1)) and e==GCD(e,p-1)*GCD(e,q-1)*GCD(e,r-1)
assert len(message)>L and len(message)<2*L
assert b'SUSCTF' in message
m=bytes_to_long(pad(message))
c=pow(m,e,n)
print(c)
'''
2832775557487418816663494645849097066925967799754895979829784499040437385450603537732862576495758207240632734290947928291961063611897822688909447511260639429367768479378599532712621774918733304857247099714044615691877995534173849302353620399896455615474093581673774297730056975663792651743809514320379189748228186812362112753688073161375690508818356712739795492736743994105438575736577194329751372142329306630950863097761601196849158280502041616545429586870751042908365507050717385205371671658706357669408813112610215766159761927196639404951251535622349916877296956767883165696947955379829079278948514755758174884809479690995427980775293393456403529481055942899970158049070109142310832516606657100119207595631431023336544432679282722485978175459551109374822024850128128796213791820270973849303929674648894135672365776376696816104314090776423931007123128977218361110636927878232444348690591774581974226318856099862175526133892
'''
A n a l y s i s Analysis Analysis
可以明显地看到
assert isPrime(GCD(e,p-1)) and isPrime(GCD(e,q-1)) and isPrime(GCD(e,r-1)) and e==GCD(e,p-1)*GCD(e,q-1)*GCD(e,r-1)
e ∣ p − 1 , q − 1 , r − 1 e|p-1,q-1,r-1 e∣p−1,q−1,r−1;且 e e e是由 e e e与三个素数减一的最大公因数的乘积
这就意味着 e e e与 ϕ ( n ) \phi(n) ϕ(n)不互素,那么即使我们知道了 e e e,也不能按照正常的RSA解密方式 m ≡ c d ( m o d n ) m\equiv c^d\pmod n m≡cd(modn)求解
所以目前有两个难点,一是 e e e是未知大小的,二是如何在 e e e与 ϕ ( n ) \phi(n) ϕ(n)非互质的情况下求解RSA
G e t e Get~e Get e
p − 1 , q − 1 , r − 1 p-1,q-1,r-1 p−1,q−1,r−1都可以先分解程成一些较小的素数和一两个较大的整数(无法继续分解了)
下面以求得 e p ep ep为例
∵ g c d ( e , ϕ ( n ) ) ≠ 1 \because gcd(e,\phi(n))\neq1 ∵gcd(e,ϕ(n))=1,且 $ t^{p-1}\equiv t^{\frac{ep\cdot(p-1)}{ep}} \equiv (t^{ep}\pmod p)^{\frac{p-1}{ep}}\equiv 1\pmod p $;(费马小定理)
其中 t t t是任意一个不是 p p p倍数的整数, e p ep ep是 e e e和 p − 1 p-1 p−1的最大公因数
换而言之,中间的 t e p ( m o d p ) t^{ep}\pmod p tep(modp)可以用来替换成与密文 c c c相关的式子以达到求得 e e e的目的
∵ c ≡ m e ( m o d n ) ≡ m e p ⋅ e q ⋅ e r ( m o d p ⋅ q ⋅ r ) \because c\equiv m^e\pmod n\equiv m^{ep\cdot eq\cdot er}\pmod {p\cdot q\cdot r} ∵c≡me(modn)≡mep⋅eq⋅er(modp⋅q⋅r)
∴ c ( m o d p ) ≡ ( m e p ( m o d p ) ) e q ⋅ e r ( m o d p ) \therefore c\pmod p\equiv (m^{ep}\pmod p)^{eq\cdot er}\pmod p ∴c(modp)≡(mep(modp))eq⋅er(modp)
这里只要是正确的 e p ep ep,把 c c c和 e p ep ep代入费马小定理的式子中会同余于 1 1 1
这就意味着我们只需要爆破出满足 c p − 1 e p ≡ 1 ( m o d p ) c^{\frac{p-1}{ep}}\equiv 1\pmod p cepp−1≡1(modp)的 e p ep ep即可
同理 e q eq eq, e r er er
实现代码
import primefac
for e_p in primefac.primefac(p-1):
if pow(c%p,(p-1)//e_p,p) == 1 and e_p != 2:
# print(e_p)
break
for e_q in primefac.primefac(q-1):
if pow(c%q,(q-1)//e_q,q) == 1 and e_q != 2:
# print(e_q)
break
for e_r in primefac.primefac(r-1):
if pow(c%r,(r-1)//e_r,r) == 1 and e_r != 2:
# print(e_r)
break
G e t p l a i n t Get~plaint Get plaint
一般的想法是AMM算法,但是根据这道题的条件AMM算法计算时间可能有几个小时,这里根据官方wp介绍的更为快捷的算法来解题
算法来源:https://eprint.iacr.org/2020/1059.pdf
算法的相关证明以及扩展详情可见上述论文
该算法的运行时间与
e
e
e的大小成线性关系(所以之后我们需要缩小
e
e
e)
这里就介绍算法过程

A l g o r i t h m 1 Algorithm~1 Algorithm 1
先令 ϕ ˙ = ϕ ( n ) e \dot\phi=\frac{\phi(n)}{e} ϕ˙=eϕ(n); g = 1 g=1 g=1
循环 g = g + 1 g=g+1 g=g+1; g E ≡ g ϕ ˙ ( m o d N ) g_E\equiv g^{\dot\phi}\pmod N gE≡gϕ˙(modN)
直到出现 g E ≠ 1 g_E\neq 1 gE=1的 g E g_E gE

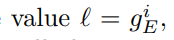
A l g o r i t h m 2 Algorithm~2 Algorithm 2
依旧令 ϕ ˙ = ϕ ( n ) e \dot\phi=\frac{\phi(n)}{e} ϕ˙=eϕ(n)
计算 d ≡ e − 1 ( m o d ϕ ˙ ) d\equiv e^{-1}\pmod {\dot\phi} d≡e−1(modϕ˙); a ≡ c d ( m o d N ) a\equiv c^d\pmod N a≡cd(modN)
判断
a
a
a转换为字节/字符类型之后,是否有价值的信息(这里就是判断是否b'SUSCTF'在其中)
若没有,进行 e e e次循环,跳出循环的条件也是上述条件
循环体: a ≡ a ⋅ g E ( m o d N ) a\equiv a \cdot g_E \pmod N a≡a⋅gE(modN)
最后满足条件的
a
a
a就是flag
代码实现
# 算法一
phi = phi_n // e
g = 1
g_E = pow(g,phi,n)
while g_E == 1:
g = g + 1
g_E = pow(g,phi,n)
# print(g,g_E)
# 算法二
d = gmpy2.invert(e,phi)
a = pow(c,d,n)
for _ in tqdm(range(now_e)):
flag = a
if b"SUSCTF" in long_to_bytes(flag):
print(long_to_bytes(flag))
break
else:
a = a * g_E % n
N e c e s s a r y M a j o r i z a t i o n Necessary~Majorization Necessary Majorization
F i r s t First First
在
A
l
g
o
r
i
t
h
m
2
Algorithm~2
Algorithm 2中需要进行
e
e
e次循环,而目前e=757*66553*5156273=259776235785533;肉眼可见的太大了,可能没几年跑不完
那就除去 r r r来缩小 e e e,显然不能简单地在 e e e上除去 r r r就完了,还需要对 c c c, ϕ ( n ) \phi(n) ϕ(n)作改变
令 ϕ ( n ) = ( p − 1 ) ⋅ ( q − 1 ) \phi(n)=(p-1)\cdot (q-1) ϕ(n)=(p−1)⋅(q−1); N = N r N = \frac{N}{r} N=rN
由 d r ⋅ e r ≡ 1 ( m o d ϕ ( n ) ) d_{r}\cdot e_r\equiv 1\pmod {\phi(n)} dr⋅er≡1(modϕ(n))求得逆元 d r d_{r} dr
∵ c ≡ m e r ⋅ e p ⋅ e q ( m o d p ⋅ q ⋅ r ) \because c\equiv m^{e_r\cdot e_p\cdot e_q}\pmod {p\cdot q\cdot r} ∵c≡mer⋅ep⋅eq(modp⋅q⋅r)
∴ c d r ≡ ( m e r ⋅ d r ) e p ⋅ e q ( m o d N ) \therefore c^{d_r}\equiv (m^{e_r\cdot d_r})^{e_p\cdot e_q}\pmod N ∴cdr≡(mer⋅dr)ep⋅eq(modN)
所以计算 c ≡ c d r ( m o d N ) c\equiv c^{d_{r}}\pmod N c≡cdr(modN)得到的 c c c即是 e e e变化后对应的 c c c
S e c o n d Second Second
在RSA加密过程中程序对明文作了填充,也就是pad()函数
仔细观察也就是简单在明文十六进制位上不断添 0 0 0直到整体的十六进制位达到 3 ⋅ L 3\cdot L 3⋅L位
而且真实的明文长度处于$ L$到 2 ⋅ L 2\cdot L 2⋅L之间(此时 m m m小于 N N N)
assert len(message)>L and len(message)<2*L
也就是说,至少填充了 L L L位的十六进制,而总共 3 ⋅ L 3\cdot L 3⋅L的十六进制位已经大于了 N N N
也就意味着这样已经造成了明文丢失,且无法恢复明文
那么就需要把填充的十六进制位数消除,至少消去 L L L位的十六进制(其余的填充位因为未知大小所以就不管了),因为 2 ⋅ L 2\cdot L 2⋅L的十六进制位是小于 N N N的,可以就此恢复明文
仔细观察pad()函数
def pad(s):
if len(s)<3*L:
s+=bytes(3*L-len(s))
return s
实际上我们使用二进制更多一些,这里1 byte是
8
8
8个二进制位,那么实际有
2
8
⋅
L
2^{8\cdot L}
28⋅L多余的数
原来的pad()函数相当于
m
=
m
⋅
2
8
⋅
L
m=m\cdot 2^{8\cdot L}
m=m⋅28⋅L;代入RSA加密之后,可以这样看
c ≡ c m ⋅ c p a d ≡ c m ⋅ 2 8 ⋅ L ⋅ e ( m o d N ) c\equiv c_m\cdot c_{pad}\equiv c_m\cdot 2^{8\cdot L\cdot e}\pmod N c≡cm⋅cpad≡cm⋅28⋅L⋅e(modN)
那么为了消去pad的影响,我们直接乘上padding的逆元d=gmpy2.invert(pow(2,8*L*e,N),N)
其中,这里的 e e e和 N N N可以是除去 r r r之后的,也可以是除去 r r r之前的
实现代码
c = c * gmpy2.invert(pow(2,8 * L * e,n),n) % n
S o l v i n g c o d e Solving~code Solving code
from Crypto.Util.number import *
import gmpy2,primefac
from tqdm import tqdm
L = 128
p = 127846753573603084140032502367311687577517286192893830888210505400863747960458410091624928485398237221748639465569360357083610343901195273740653100259873512668015324620239720302434418836556626441491996755736644886234427063508445212117628827393696641594389475794455769831224080974098671804484986257952189021223
q = 145855456487495382044171198958191111759614682359121667762539436558951453420409098978730659224765186993202647878416602503196995715156477020462357271957894750950465766809623184979464111968346235929375202282811814079958258215558862385475337911665725569669510022344713444067774094112542265293776098223712339100693
r = 165967627827619421909025667485886197280531070386062799707570138462960892786375448755168117226002965841166040777799690060003514218907279202146293715568618421507166624010447447835500614000601643150187327886055136468260391127675012777934049855029499330117864969171026445847229725440665179150874362143944727374907
c = 2832775557487418816663494645849097066925967799754895979829784499040437385450603537732862576495758207240632734290947928291961063611897822688909447511260639429367768479378599532712621774918733304857247099714044615691877995534173849302353620399896455615474093581673774297730056975663792651743809514320379189748228186812362112753688073161375690508818356712739795492736743994105438575736577194329751372142329306630950863097761601196849158280502041616545429586870751042908365507050717385205371671658706357669408813112610215766159761927196639404951251535622349916877296956767883165696947955379829079278948514755758174884809479690995427980775293393456403529481055942899970158049070109142310832516606657100119207595631431023336544432679282722485978175459551109374822024850128128796213791820270973849303929674648894135672365776376696816104314090776423931007123128977218361110636927878232444348690591774581974226318856099862175526133892
n = p * q * r
# 恢复e
for e_p in primefac.primefac(p-1):
if pow(c%p,(p-1)//e_p,p) == 1 and e_p != 2:
# print(e_p)
break
for e_q in primefac.primefac(q-1):
if pow(c%q,(q-1)//e_q,q) == 1 and e_q != 2:
# print(e_q)
break
for e_r in primefac.primefac(r-1):
if pow(c%r,(r-1)//e_r,r) == 1 and e_r != 2:
# print(e_r)
break
e = e_p * e_q * e_r
# print(e_p,e_q,e_r)
phi_n = (p - 1) * (q - 1) * (r - 1)
# print(e)
# 消除L位的十六进制的padding(在删除r之前)
c = c * gmpy2.invert(pow(2,8 * L * e,n),n) % n
# 缩小e:删除r以及更改各个指标的受r的影响
e = e // e_r
phi_n_without_r = (p - 1) * (q - 1)
n = n // r
d1 = gmpy2.invert(e_r,phi_n_without_r)
c = pow(c,d1,n)
# 在删除r后消除padding
# c = c * gmpy2.invert(pow(2,8 * L * now_e,n),n) % n
# 算法一
phi = phi_n_without_r // e
g = 1
g_E = pow(g,phi,n)
while g_E == 1:
g = g + 1
g_E = pow(g,phi,n)
# print(g,g_E)
# 算法二
d = gmpy2.invert(e,phi)
a = pow(c,d,n)
for _ in tqdm(range(e)):
flag = a
if b"SUSCTF" in long_to_bytes(flag):
print()
print(long_to_bytes(flag))
break
else:
a = a * g_E % n
最后得到flag
























 445
445











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










