逆元的应用

1.逆元解释:
逆元定义:

来自一个大佬的通俗解释:

逆元基本应用1

我们知道对于取余运算，有以下性质:

但是唯独除法是不满足的！

现证明除法不满足:

而对于一些题目，我们必须在中间过程中进行求余，否则数字太大，电脑存不下，那如果这个算式中出现除法，我们就需要逆元了。

现在就要在回到刚才的问题了，除以一个数等于乘上这个数的倒数，在除法取余的情况下，就是乘上这个数的逆元。

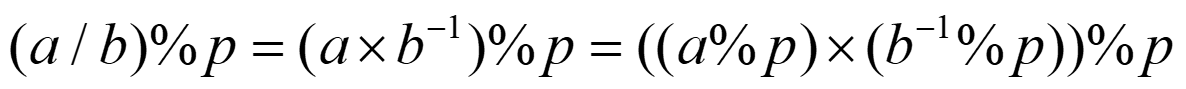
这样就把除法，完全转换为乘法了！

逆元的五种求法

1.暴力求解，易理解但是时间复杂度巨大，上代码：

int Inverse_element(int a, int p)
{
    a = a % p;
    int flag = 0;
    int result;
    for (int i = 1; i < 100000; i++)
    {
        flag = 0;
        for (int j = 1; j < 100000; j++)
        {
            if (a * i == 1 + p * j)
            {
                result = i;
                flag = 1;
                break;
            }
        }
        if (flag == 1)
        {
            break;
        }
    }
    return result;
}

2.扩展欧几里得算法
扩展欧几里得算法定义：

模数可以不为质数，满足gcd(a,b)=1即可：

当gcd(a,b)=1时，代入extend_gcd(a,b,x,y)，得到的非负的x值，就是上面的a-1
时间复杂度$O(log(n))$

ll exgcd(ll a, ll b, ll &x, ll &y)
{
	if (b == 0)
	{
		x = 1, y = 0;
		return a;
	}
	ll d, x1, y1;
	d = exgcd(b, a % b, x1, y1);
	x = y1;
	y = x1 - a / b * y1;
	return d;
}
ll inverse(ll a, ll b, ll &x, ll &y)
{
	if (__gcd(a, b) != 1) return -1;
	else
	{
		exgcd(a, b, x, y);
		return (x % b + b) % b;
	}
}

3.欧拉定理和费马小定理：
欧拉定理在数论中，欧拉定理,(也称费马-欧拉定理)是一个关于同余的性质。欧拉定理表明，若n,a为正整数，且n,a互质，则:

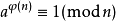
φ(n)为欧拉函数（$1-n中与n互质的数的个数。$（1与任何数互质））。

费马小定理：(只适用于模数为质数的情况 )
当 $n$为质数且a不为n的倍数时，φ(n)=n-1，所以式子变成:

两边同时除a得：

所以得：

用快速幂求一下，复杂度$O(logn)$

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n, p;
ll qpow(ll a, ll b, ll mod)
{
	ll ans = 1;
	while (b)
	{
		if (b & 1) ans = (ans * a) % mod;
		a = (a * a) % mod;
		b >>= 1;
	}
	return ans % mod;
}

int main()
{
	scanf("%d%d", &n, &p);
	for (int i = 1; i <= n; i++)
	{
		cout << qpow(i, p - 2, p) << "\n";
	}
	return 0;
}

4.线性递推逆元（神奇小饼干法）
只适用于模数为质数的情况
当p为质数时有:

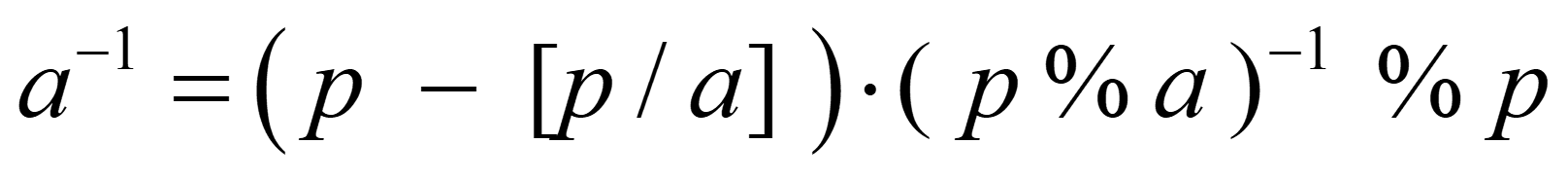
证明：
并且inverse[0]=0,inverse[1]=1,递归或循环从2开始

写成算法就是一个递归，到1为止，因为1的逆元就是1。

int inv(int t, int p) {
    return t == 1 ? 1 : (p - p / t) * inv(p % t, p) % p;
}

这个方法复杂度是O(n)，但并不是说比前两个差，它可以在O(n)的复杂度内算出n个数的逆元，上面的算法加一个记忆性搜索就行了。

int inv(int t, int p) {
    return INV[t] = t == 1 ? 1 : (p - p / t) * inv(p % t, p) % p;
}

#include <bits/stdc++.h>
using namespace std;
const int N = 3e6 + 19;
typedef long long ll;
ll n, p;
ll ans[N];


int main()
{
	scanf("%d%d", &n, &p);
	ans[1] = 1;
	for (int i = 2; i <= n; i++)
	{
		ans[i] = (p - p / i) * ans[p % i] % p;
	}
	for (int i = 1; i <= n; i++)
	{
		cout << ans[i] << "\n";
	}
	return 0;
}

5.阶乘逆元法
只适用于模数为质数的情况

#include<cstdio>
#define ll long long
using namespace std;
ll mul(ll a,ll b,ll mod) //快速幂模板
{
  ll ans=1;
  while(b)
    {
    	if(b&1) ans=ans*a%mod;
    	a=(a*a)%mod;
    	b>>=1;
    }
  return ans%mod;
}
ll n,p;
ll c[5000010]={1};
ll f[5000010];
int main()
{
  scanf("%lld%lld",&n,&p);
  for(int i=1;i<=n;i++)
    c[i]=(c[i-1]*i)%p;
    
  f[n]=mul(c[n],p-2,p); //获得inv(n!)
  
  for(int i=n-1;i>=1;i--) //递推阶乘的逆元
    f[i]=(f[i+1]*(i+1))%p;
    
  for(int j=1;j<=n;j++) //转化并输出
    printf("%lld\n",(f[j]*c[j-1])%p);
}