前言:参考背包问题九讲GitHub - tianyicui/pack: 背包问题九讲
1. 01背包问题
题目:
思路:
每种物品仅有一件,可以选择放或不放。设 F [i, v] 表示前 i 件物品恰放入一个容量为 v 的背包可以获得的最大价值。
放: F [i, v] = F [i-1, v]
不放:F [i, v] = F [i-1, v-
]+
状态转移方程:F [i, v] = max( F [i-1, v] , F [ i-1, v-
] +
}
代码:
public static int knapsack(int[] C, int[] W, int V, int N) {
// 初始化dp数组,dp[i][j]表示前i个物品,背包容量为j时的最大价值
int[][] dp = new int[N + 1][V + 1];
// 当背包容量为0时,无论有多少物品,最大价值都为0
for (int i = 0; i <= N; i++) {
dp[i][0] = 0;
}
// 当没有物品可选时,无论背包容量有多少,最大价值都为0
for (int j = 0; j <= V; j++) {
dp[0][j] = 0;
}
// 填充dp数组,从前往后遍历每个物品,从小到大遍历背包容量
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= V; j++) {
// 如果当前物品的重量小于等于背包容量,可以考虑将其放入背包
if (j >= W[i - 1]) {
// 如果放入当前物品,可以得到的最大价值比不放入当前物品的最大价值更高,则放入当前物品
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - W[i - 1]] + C[i - 1]);
} else {
// 如果当前物品的重量大于背包容量,无法放入背包,最大价值等于上一个物品的最大价值
dp[i][j] = dp[i - 1][j];
}
}
}
// 返回最大价值,即dp[N][V]
return dp[N][V];
}时间复杂度为O(NV),空间复杂度为O(NV)。
优化空间复杂度:
先考虑上面的基本思路如何实现,肯定是有一个主循环 i (1 . . . N) ,每次算出来
二维数组 F [i, 0 . . . V ] 的所有值。
但是,如果只用一个数组 F [0 . . . V ],能不能保证第 i次循环结束后 F [v] 中表示的就是我们定义的状态 F [i, v] 呢?
F [i, v]是由放和不放两个子问题递推来解决的。
如何保证在第 i 次主循环中推 F [i, v] 时能够取用 F [i-1, v]和 F [i-1, v-
+
]的值呢?
递减顺序计算 F [v]
为什么?
F[i ,v]表示前 i 件物品恰放入一个容量为 v 的背包可以获得的最大价值
F[v]表示物品恰放入一个容量为 v 的背包可以获得的最大价值
可以理解成F[ i , v] 是在不同的F[ v ] 情况下操作。
如果是是顺序,那么上一个F[ v ]的状态会被改变。就变成了 F [i, v] 由 F [i, v-
],所以需要逆序。
public static int knapsack(int[] C, int[] W, int V, int N) {
// 初始化dp数组,dp[i]表示背包容量为i时的最大价值
int[] dp = new int[V + 1];
// 从前往后遍历每个物品,从小到大遍历背包容量
for (int i = 1; i <= N; i++) {
// 从后往前遍历背包容量,保证计算dp[j]时使用的是上一个物品未更新的dp[j-W[i-1]]
for (int j = V; j >= W[i - 1]; j--) {
// 如果放入当前物品,可以得到的最大价值比不放入当前物品的最大价值更高,则放入当前物品
dp[j] = Math.max(dp[j], dp[j - W[i - 1]] + C[i - 1]);
}
}
// 返回最大价值,即dp[V]
return dp[V];
}初始化的细节问题
有的题目要求“恰好装满背包”时的最优解,有的题目则并没有要求必须把背包装满。一种区别
这两种问法的实现方法是在初始化的时候有所不同。

背包问题中,初始化为负无穷表示当前状态不可行或无法达成,因此当背包问题初始化为负无穷时,意味着当前状态无法通过选择物品来达到。
在恰好装满的背包问题中,我们需要选取一些物品,使得它们的总重量恰好等于背包的容量。因此,如果我们将背包问题的初始状态设为0,表示背包中没有物品,那么如果在后续的状态中我们得到了一个总重量为0的解,那么这个解并不一定是合法的恰好装满的解,因为这个解也可以是什么都没有选的解。因此,我们将背包问题的初始状态设为负无穷,确保了只有当选取的物品总重量为背包容量时,才能得到合法的解。
如果还是不理解:假设物品的价值是负数(如偷东西被处罚),那么最大价值会是0(也就是什么都不选)。但是恰好装满会因为初始化都是-导致必须选。
F [i, v] = max( F [i-1, v] , F [i-1, v-
]+
}
代码:
public static int knapsack(int[] C, int[] W, int V, int N) {
// 初始化dp数组,dp[i][j]表示前i个物品,恰好装满容量为j的背包时的最大价值
int[][] dp = new int[N + 1][V + 1];
// 当背包容量为0时,无论有多少物品,最大价值都为0
for (int i = 0; i <= N; i++) {
dp[i][0] = 0;
}
// 当没有物品可选时,无论背包容量有多少,最大价值都为负无穷(表示无法达到)
for (int j = 1; j <= V; j++) {
dp[0][j] = Integer.MIN_VALUE;
}
// 填充dp数组,从前往后遍历每个物品,从小到大遍历背包容量
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= V; j++) {
// 如果当前物品的重量小于等于背包容量,可以考虑将其放入背包
if (j >= W[i - 1]) {
// 如果放入当前物品,可以得到的最大价值比不放入当前物品的最大价值更高,则放入当前物品
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - W[i - 1]] + C[i - 1]);
} else {
// 如果当前物品的重量大于背包容量,无法放入背包,最大价值等于上一个物品的最大价值
dp[i][j] = dp[i - 1][j];
}
}
}
// 如果背包能够恰好装满,返回最大价值,否则返回0(表示无法恰好装满)
return dp[N][V] > 0 ? dp[N][V] : 0;
}2.完全背包问题
题目:
a.暴力完全背包问题:
这个问题非常类似于 01 背包问题,所不同的是每种物品有无限件。
也就是从每种物品的角度考虑,与它相关的策略已并非取或不取两种,而是有取 0 件、取 1 件、取 2件......直至取[V /] 件等许多种。
如果仍然按照解 01 背包时的思路,令 F [i, v] 表示前 i 种物品恰放入一个容量为 v的背包的最大权值。仍然可以按照每种物品不同的策略写出状态转移方程。
F [i, v] = max( F [i-1, kv] , F [i-1, v-k
] +k
}
在这其中我们需要3个for循环 :
for1 : 完成i种物品的循环
for2 : 完成容量为j的循环
for3 : k个i种物品的循环
public static int completeKnapsack(int[] C, int[] W, int V, int N) {
// 初始化dp数组,dp[i][j]表示前i个物品,容量为j的背包的最大价值
int[][] dp = new int[N + 1][V + 1];
// 从前往后遍历每个物品
for (int i = 1; i <= N; i++) {
// 从小到大遍历背包容量
for (int j = 1; j <= V; j++) {
// 枚举将当前物品放入背包的次数
for (int k = 0; k <= j / W[i - 1]; k++) {
// 计算将当前物品放入背包k次时的最大价值
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - k * W[i - 1]] + k * C[i - 1]);
}
}
}
// 返回最大价值,即dp[N][V]
return dp[N][V];
}时间复杂度为O(NV^2),空间复杂度为O(NV)
b.简单优化
若两件物品 i、j 满足,且
,则将可以将物品 j 直接去掉,不用考虑。
任何情况下都可将价值小费用高的 j 换成物美价廉的i,得到的方案至少不会更差。
c.转化为 01 背包问题求解
考虑到第 i 种物品最多选 件,于是可以把第 i 种物品转化为
件费用及价值均不变的物品,然后求解这个 01 背包问题。
但是没有改进时间复杂度。
但是可以想到更高效的转化方法(二进制):
把第 i 种物品拆成费用为,价值为
的若干物品。
这样一来就把每种物品拆成 O() 件物品.
public static int completeKnapsack(int[] C, int[] W, int V, int N) {
// 初始化dp数组,dp[j]表示容量为j的背包的最大价值
int[] dp = new int[V + 1];
// 从前往后遍历每个物品
for (int i = 1; i <= N; i++) {
// 将当前物品看作是01背包问题中的一个物品,将其转化为01背包问题求解
int count = Math.min(V / W[i - 1], (int) Math.pow(2, Math.floor(Math.log(V / W[i - 1]) / Math.log(2))));
int[] C1 = new int[count];
int[] W1 = new int[count];
for (int j = 0; j < count; j++) {
C1[j] = (j + 1) * C[i - 1];
W1[j] = (j + 1) * W[i - 1];
}
// 将当前物品转化为01背包问题后,使用01背包问题的解法更新dp数组
for (int j = V; j >= W[i - 1]; j--) {
for (int k = 0; k < count && j >= W1[k]; k++) {
dp[j] = Math.max(dp[j], dp[j - W1[k]] + C1[k]);
}
}
}
// 返回最大价值,即dp[V]
return dp[V];
}d.O(V N ) 的算法
伪代码:
这个伪代码与 01 背包问题的一维空间代码只有 v 的循环次序不同而已。
为什么呢?
首先想想为什么 01 背包中要按照 v 递减的次序来循环。
让 v 递减是为了保证第 i 次循环中的状态 F [i, v] 是由状态 F [i, v] 由 F [i-1, v-],如果是顺序会怎么样?
F [i, v] 由 F [i, v-]递推而来。刚好满足题目中的可以多次选择同一件商品。
当然也可以通过常规思路来:
状态方程::F [i, v] = max( F [i-1, v] , F [ i, v-
] +
}
将这个方程用一维数组实现,便得到了上面的伪代码。
public static int completeKnapsack(int[] C, int[] W, int V, int N) {
// 初始化dp数组,dp[j]表示容量为j的背包的最大价值
int[] dp = new int[V + 1];
// 从前往后遍历每个物品
for (int i = 1; i <= N; i++) {
// 将当前物品看作是01背包问题中的若干个物品,每个物品的数量为2的幂次方
for (int k = 1; k <= V / W[i - 1]; k *= 2) {
int cnt = Math.min(k, V / W[i - 1] - k + 1);
int[] C1 = new int[cnt];
int[] W1 = new int[cnt];
for (int j = 0; j < cnt; j++) {
C1[j] = j * C[i - 1];
W1[j] = j * W[i - 1];
}
// 使用01背包问题的一维空间顺序更新dp数组
for (int j = V; j >= W[i - 1]; j--) {
for (int l = 0; l < cnt && j >= W1[l]; l++) {
dp[j] = Math.max(dp[j], dp[j - W1[l]] + C1[l]);
}
}
}
}
// 返回最大价值,即dp[V]
return dp[V];
}3.多重背包问题
题目:

基本思路:

public static int multipleKnapsack(int[] C, int[] W, int[] M, int V, int N) {
// 初始化dp数组,dp[j]表示容量为j的背包的最大价值
int[] dp = new int[V + 1];
// 从前往后遍历每个物品
for (int i = 1; i <= N; i++) {
// 将当前物品转化为若干个01背包问题中的物品
for (int k = 1; k <= M[i - 1]; k *= 2) {
int cnt = Math.min(k, M[i - 1] - k + 1);
int[] C1 = new int[cnt];
int[] W1 = new int[cnt];
for (int j = 0; j < cnt; j++) {
C1[j] = j * C[i - 1];
W1[j] = j * W[i - 1];
}
// 将当前物品的若干个01背包问题中的物品放入完全背包问题中求解
for (int j = V; j >= W[i - 1]; j--) {
for (int l = 0; l < cnt && j >= W1[l]; l++) {
dp[j] = Math.max(dp[j], dp[j - W1[l]] + C1[l]);
}
}
}
}
// 返回最大价值,即dp[V]
return dp[V];
}时间复杂度为O(NVMlogV),空间复杂度为O(V)
转化为 01 背包问题:
既然我们可以将他转化为完全背包那么同样也可以转化为01背包。
同样也可以使用二进制的方法来降低复杂度。
public static int multipleKnapsack(int[] C, int[] W, int[] M, int V, int N) {
// 初始化dp数组,dp[j]表示容量为j的背包的最大价值
int[] dp = new int[V + 1];
// 从前往后遍历每个物品
for (int i = 1; i <= N; i++) {
// 将当前物品转化为若干个01背包问题中的物品
int k = 1; // 当前物品的数量
while (k <= M[i - 1]) {
int cnt = Math.min(M[i - 1] - k + 1, k);
int[] C1 = new int[cnt];
int[] W1 = new int[cnt];
for (int j = 0; j < cnt; j++) {
C1[j] = (j + 1) * C[i - 1];
W1[j] = (j + 1) * W[i - 1];
}
// 使用01背包问题的二进制优化方法更新dp数组
for (int j = V; j >= W1[0]; j--) {
for (int l = 0; l < cnt && j >= W1[l]; l++) {
dp[j] = Math.max(dp[j], dp[j - W1[l]] + C1[l]);
}
}
k <<= 1; // 将当前物品的数量翻倍
}
}
// 返回最大价值,即dp[V]
return dp[V];
}时间复杂度为O(NVlogM),空间复杂度为O(V)
4.分组的背包问题
问题:

思路:
对于每组物品是选择本组的某一件,还是一件都不选。
所以此时F 应该是第k组的的最大价值。
F[i][j]表示在前i组物品中选取总重量不超过j的物品能够得到的最大价值。
F [k, v] = max( F [k-1, v] , F [ k-1, v-
] +
| item i
group k}
/**
*@param group 每个物品所在的组
*@param G 组的数量
*/
public static int groupKnapsack(int[] C, int[] W, int[] group, int V, int G, int N) {
// 初始化dp数组,dp[i][j]表示在前i组物品中选取总重量不超过j的物品能够得到的最大价值
int[][] dp = new int[G + 1][V + 1];
// 从前往后遍历每个组
for (int g = 1; g <= G; g++) {
// 遍历当前组中的每个物品,使用01背包问题的解法更新dp数组
for (int i = 0; i < N; i++) {
if (group[i] == g) {
for (int j = V; j >= W[i]; j--) {
dp[g][j] = Math.max(dp[g][j], dp[g][j - W[i]] + C[i]);
}
}
}
// 使用dp[g-1][j]的值更新dp[g][j]
for (int j = 0; j <= V; j++) {
dp[g][j] = Math.max(dp[g][j], dp[g - 1][j]);
}
}
// 返回最大价值,即dp[K][V]
return dp[G][V];
}时间复杂度为O(NGV),空间复杂度为O(GV)
空间优化:
思路参考01背包思路优化
public static int groupKnapsack(int[] C, int[] W, int[] group, int V, int G, int N) {
// 初始化dp数组,dp[j]表示选取总重量不超过j的物品能够得到的最大价值
int[] dp = new int[V + 1];
// 从前往后遍历每个组
for (int g = 1; g <= G; g++) {
// 遍历当前组中的每个物品,使用01背包问题的解法更新dp数组
for (int i = 0; i < N; i++) {
if (group[i] == g) {
for (int j = V; j >= W[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - W[i]] + C[i]);
}
}
}
}
// 返回最大价值,即dp[V]
return dp[V];
}时间复杂度为O(NGV),空间复杂度为O(V)
总结:
这里是背包九讲文末的一段话:

更多的背包问题请参考GitHub - tianyicui/pack: 背包问题九讲







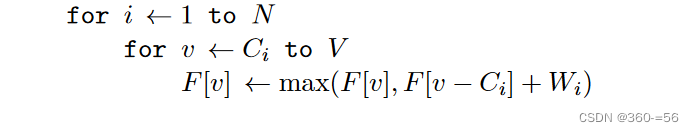














 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








