位于NOI考纲提高组的【7】级算法
【7】求强联通分量算法
【7】强连通分量的缩点算法
【7】求割点、割边算法
认识Tarjan算法
一种由Robert Tarjan提出的求解有向图强连通分量的线性时间的算法。
001/ 强连通分量
Tarjan算法的最普遍功能
一些前置知识
在有向图中:
连通:两个点互相可达
强连通图:图中任意两点互相可达
强连通分量:有向图的极大连通子图(子图中任意两点互相可达,且不能再添加点进入),也就是以全部强连通的点构成的子图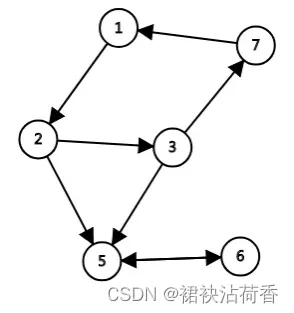
上图中有两个强连通分量,分别是(1, 2, 3, 7)和(5, 6)。
看个例题
消息的传递
问题描述
时间:三国时期 ;
地点:许昌;人物:曹操,你。
事件:
起因:曹操得知许昌城里有n(n )个袁绍的奸细。(他们编号为1到n,奸细间存在着一 种消息传递关系,即若C[i][j]=1,表示奸细i能直接把消息传给奸细j)。
经过:曹操想发布一个假消息,需要传达给所有奸细。曹操命令你来负责消息的发布。
结果:聪明的你把消息传递给了很少的几个奸细,就使所有奸细都得到了这个消息。
问:最少传递给几个奸细就能完成任务?
输入格式
第一行为N,第二行至第N+1行为N*N的矩阵(若第I行第J列为1,则奸细I能将消息直接传递给奸细J,若第I行第J列为0,则奸细I不能直接将消息传给J )
输出格式
你最少要传递的奸细的个数
样例输入
8
0 0 1 0 0 0 0 0
1 0 0 1 0 0 0 0
0 1 0 1 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 1 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 1 0 0 0 1
0 0 0 0 0 0 1 0
样例输出
2
在这道题中,我们将消息传递关系建图,边 ( i , j ) \left(i, j\right) (i,j) 表示 i i i 能给 j j j传递消息。由于强连通分量内节点互相可达,所以在同一强连通分量中的“奸细”中只需要选择一个就可以使整个子图内的“奸细”都得知消息。
将每个强连通分量都缩成一个节点,再重新进行建边。此时建出的图是一个有向无环图。最后只需要统计入度为0的节点数量就是最终的答案,因为只要一个点有入度,它就一定可以由其他节点到达。
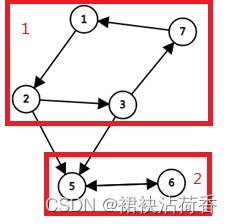
此题中的查找强连通分量然后缩点就是此类题型的基本做法。
接下来讨论核心算法。
求强连通分量的两个方法
-
Kosaraju算法
Kosaraju算法的核心在于首先将图反转进行dfs,取强连通分量的后序排列。
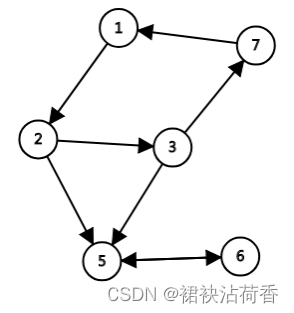
回到上图,当使用dfs寻找强连通分量时,如果一开始从1开始dfs,则当遍历到2时路径形成了一个分叉,为了确认该强连通分量,我们希望2不走到5节点上去,而是继续到3,然后到7,最后形成完美的闭环。
那么正向的dfs该如何做到规避掉这样的路径分叉呢?
由于反转图和正向图的强连通分量情况相同,我们将图反转,dfs求出每一个节点的后序编号。此时从任何地方开始遍历,强连通分量(1, 2, 3, 7)都将处于序列的末尾。
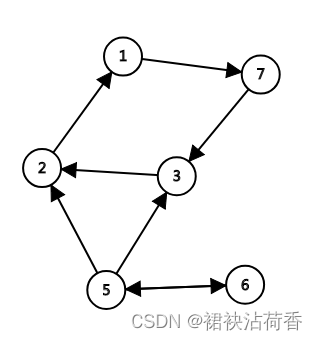
(反转图)
此时再按照这个后序编号进行正向图的dfs,就可以确保强连通分量(5, 6)在(1, 2, 3, 7)之前被标记到,以保证搜索到2或3时会跳转到5节点。
//消息的传递 Kosaraju算法
#include <bits/stdc++.h>
using namespace std;
long long n, m, pos, scc, lst[1007], vis[1007], d[1007];
bool a[1007][1007];
long long dfs (long long p) { //查找反图
vis[p] = 1;
for (long long i = 1; i <= n; i ++)
if (a[p][i] && !vis[i]) dfs (i);
lst[++ pos] = p;
}
long long dfs1 (long long p) { //正向查找
vis[p] = scc;
for (long long i = 1; i <= n; i ++)
if (a[i][p] && !vis[i]) dfs1 (i);
}
int main () {
scanf ("%lld", &n);
for (long long i = 1; i <= n; i ++) {
for (long long j = 1; j <= n; j ++) {
scanf ("%d", &a[i][j]);
}
}
for (long long i = 1; i <= n; i ++) {
vis[i] = false;
}
for (long long i = 1; i <= n; i ++) {
if (!vis[i]) dfs(i);
}
for (long long i = 1; i <= n; i ++) {
vis[i] = false;
}
scc = 1;
for (long long i = n; i >= 1; i --) {
if (!vis[lst[i]]) {
dfs1 (lst[i]);
scc ++;
}
}
//缩点
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= n; j ++) {
if ((vis[i] != vis[j]) && (a[i][j])) d[vis[j] - 1] = 1;
}
}
int tot = 0;
//统计答案
for (int i = 1; i <= scc - 1; i ++) {
if (!d[i]) tot ++;
}
printf ("%lld", tot);
return 0;
}
-
Tarjan算法
核心在于利用搜索树查找强连通分量。
dfs时,我们通过一个节点往它所连接的节点搜索,因此将搜索的路径画出来就是一棵树,且父亲节点指向子孙节点,这样的树一定是原图的一个子图。当然还会有多出来的边。不难发现,由于搜索树是从上到下的有向无环图,所以强连通分量(环)也就只会出现在多出来的从子孙指向其祖先的边上。从该祖先到该子孙的路径就是这个强连通分量。在进行
dfs的过程中,记录两个信息:dfn[u]表示被搜索到的次序low[u]表示u能够到达的节点中最小的dfn[v]在搜索过程中,从
u到v的节点有三种情况:-
v未被访问过:搜索v,然后用low[v]更新low[u]。 -
v已经被访问过,还在栈中:说明v还没有更新完它的强连通分量,用dfn[v]更新low[u] -
v已经被访问过,但不在栈中:说明v已经完成它的使命,被栈弹出不会回溯到了,因此不做任何操作。
另:在搜索过程中,将搜索栈和节点是否进栈用instack[] 数组表示出来,更方便查询。
在一个强连通分量中,有且仅有一个节点u满足dfn[u] == low[u],它是连通分量中最小,也是第一个被查询到的点。判断该节点,则栈中它之上的节点都是它的连通分量中的节点,对它们进行统一标记并编号。
-
```cpp
//消息的传递 Tarjan算法
#include <bits/stdc++.h>
using namespace std;
int scc, n, a[1007][1007], d[1007], id[1007];
int dfn[1007], low[1007], vis[1007], instack[1007], cnt;
stack <int> s;
void Tarjan (int u) {
dfn[u] = low[u] = ++cnt;
s.push (u);
vis[u] = 1;
instack[u] = 1;
for (int v = 1; v <= n; v ++) {
if (a[u][v]) {
if (!vis[v]) { //v未被访问过
Tarjan (v);
low[u] = min (low[u], low[v]);
}
else if (instack[v]) { //v被访问过,且还在栈中
low[u] = min (low[u], dfn[v]);
}
}
}
//缩点
if (dfn[u] == low[u]) {
scc ++;
int v;
do {
v = s.top ();
s.pop ();
instack[v] = 0;
id[v] = scc;
} while (u != v); //u是该连通分量第一个进栈的节点
}
}
int main () {
scanf ("%d", &n);
for (long long i = 1; i <= n; i ++)
for (long long j = 1; j <= n; j ++)
scanf ("%d", &a[i][j]);
int ans = 0;
for (int i = 1; i <= n; i ++)
if (!vis[i])
Tarjan (i);
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= n; j ++)
if (id[i] != id[j] && a[i][j])
d[id[j]] = 1;
for (int i = 1; i <= scc; i ++) if (!d[i]) ans ++;
printf ("%d", ans);
return 0;
}
002/ 双连通分量
在无向图中:
割点:删除该点后这个连通子图变得不再连通。换句话说,删掉这个点这个图的极大连通分量数增加,这个点就叫割点。
割边(桥):同理,删除割边则图的极大连通分量数会增加。
在连通的无向图中:
边双连通分量:无论删去哪条边都不能使该分量不连通,也就意味着没有割边
点双连通分量:无论删去哪个点都不能使该分量不连通,意味着没有割点
- 运用Tarjan求割点
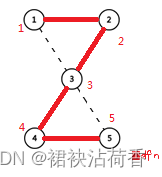
在这一张图中,3是割点。
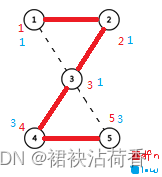
我们画出树边,然后写出每个节点的dfn和low
当一个节点u存在任何一个儿子节点v使得dfn[u]<=low[v],也就说明v不能通过任何一条路径回溯到比u更靠上的节点,所以去掉u就会把v及v的子树断开,u是割点。
但这时有一个特殊情况,就是节点u为生成树的根节点。这时只要u有两个以上的儿子,u就一定是割点。因为这时的子节点无法回溯到u更上的节点,无向图也没有横向连接两棵树的“横叉边”。
运用到Tarjan算法当中,只需要在原来的基础上,在连接树边之后判断即可。
```cpp
for (int v = 1; v <= n; v ++) {
if (a[u][v]) {
if (!vis[v]) { //v未被访问过
Tarjan (v);
low[u] = min (low[u], low[v]);
if (low[v] >= dfn[u]) {
//也可以在此处记录割点u
ans ++; //统计割点
}
else if (instack[v]) { //v被访问过,且还在栈中
low[u] = min (low[u], dfn[v]);
}
}
}
最后一定要增加一个关于特殊情况的判断,可以通过统计根节点儿子的数量完成,这里就懒得放了。
- 运用Tarjan求割边(桥)
只需要更改一处:low[v] > dfn[u]就可以了。不需要判断根节点。
不放代码了。
003/ 2-SAT
一种将逻辑限制转换为图论的思想
整个例题:
聚会
问题描述
有n对夫妻(编号0到n-1)被邀请参加一个聚会,因为场地的问题,每对夫妻中只有1人可以列席。在2n 个人中,某些人之间有着很大的矛盾(当然夫妻之间是没有矛盾的),有矛盾的2个人是不会同时出现在聚会上的。有没有可能会有n 个人同时列席?
输入格式
多组数据
n: 表示有n对夫妻被邀请 (n<= 1000)
m: 表示有m 对矛盾关系 ( m < (n - 1) * (n -1))
在接下来的m行中,每行会有4个数字,分别是 A1,A2,C1,C2
A1,A2分别表示是夫妻的编号
C1,C2 表示是妻子还是丈夫 ,0表示妻子 ,1是丈夫(C1跟C2有矛盾)
夫妻编号从 0 到 n -1
输出格式
对于每组数据:
如果存在一种n个人同时列席的情况 则输出YES
否则输出 NO
样例输入
2
1
0 1 1 1
样例输出
YES
在这道题里,每一对夫妻都有两个状态(丈夫/妻子去),而对于这许多对夫妻存在一些矛盾关系。寻找同时列席的情况的过程就可以称作 2-SAT 问题。
每一对夫妻看作一个两个元素的集合,集合 a a a的两个元素分别就为 a a a和 ¬ a \neg a ¬a, a a a表示男的去, ¬ a \neg a ¬a表示女的去。
一个矛盾关系如第 a a a个丈夫和第 b b b个妻子有矛盾,就表示为 ⟨ a , ¬ b ⟩ \left\langle a, \neg b \right \rangle ⟨a,¬b⟩
可以用位运算的方式表示出来,即 a & ¬ b = f a l s e a \& \neg b = false a&¬b=false
那么这样的式子如何转化到图论中呢?
还是刚才的那个矛盾关系,其中如果第 a a a个丈夫 a a a去了,那么第 b b b对夫妻就只有让丈夫 b b b去。同理,如果第 b b b个妻子 ¬ b \neg b ¬b去了,则第 a a a对夫妻就只有让妻子非 ¬ a \neg a ¬a去。
将这样的关系连边,即连 ( a , b ) \left( a, b \right) (a,b)和 ( ¬ a , ¬ b ) \left( \neg a, \neg b \right) (¬a,¬b)
然后使用Tarjan缩点,处在同一强连通分量里的节点就是必须同时列席的。所以,如果一对夫妻
a
a
a和
¬
a
\neg a
¬a同时出现在一个强连通分量里面,则被判断为无解。
这就是2-SAT问题的基本解决方式。
注意摸清“如果选择集合 a a a中的 u u u,则集合 b b b必须选择 v v v。连边 ( u , v ) \left( u, v \right) (u,v)
代码:
#include <bits/stdc++.h>
using namespace std;
int n, m;
vector <int> mp[2007];
void add (int u, int v) {
mp[u].push_back (v);
}
int dfn[2007], low[2007], cnt, scc, id[2007];
bool instack[2007];
stack <int> s;
void Tarjan (int u) {
dfn[u] = low[u] = ++cnt;
instack[u] = 1;
s.push (u);
int len = mp[u].size ();
for (int i = 0; i < len; i ++) {
int v = mp[u][i];
if (!dfn[v]) {
Tarjan (v);
low[u] = min (low[u], low[v]);
}
else if (instack[v]) {
low[u] = min (low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
scc ++;
int v;
do {
v = s.top ();
s.pop ();
instack[v] = 0;
id[v] = scc;
} while (v != u);
}
}
void init () {
for (int i = 0; i <= n * 2; i ++) mp[i].clear ();
memset (dfn, 0, sizeof dfn);
memset (low, 0, sizeof low);
memset (id, 0, sizeof id);
memset (instack, 0, sizeof instack);
while (!s.empty ()) s.pop ();
cnt = scc = 0;
}
bool check () {
for (int i = 0; i < n; i ++) {
if (id[i * 2] == id[i * 2 + 1]) {
return 0;
}
}
return 1;
}
int main () {
while (scanf ("%d %d", &n, &m) == 2) {
init ();
for (int i = 1; i <= m; i ++) {
int a1, a2, c1, c2;
scanf ("%d %d %d %d", &a1, &a2, &c1, &c2);
int u = a1 * 2 + c1;
int v = a2 * 2 + c2;
add (u, v ^ 1);
add (v, u ^ 1);
}
for (int i = 0; i <= n * 2 - 1; i ++) {
if (!dfn[i]) {
Tarjan (i);
}
}
if (check()) printf ("YES\n");
else printf ("NO\n");
}
return 0;
}
End.






















 1253
1253











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








