冒泡排序-Java实现

首先我们讲一下什么是冒泡排序

冒泡排序是一种常用的排序算法，我们就一个例子来说明它：小明，小军，小红，李华，四个人军训站成一排。小明身高：180，小军:169，小红：175，李华：168。如果我们要从左自右，从低到高将他们排好队。使用冒泡排序的办法那就是这样的：

 

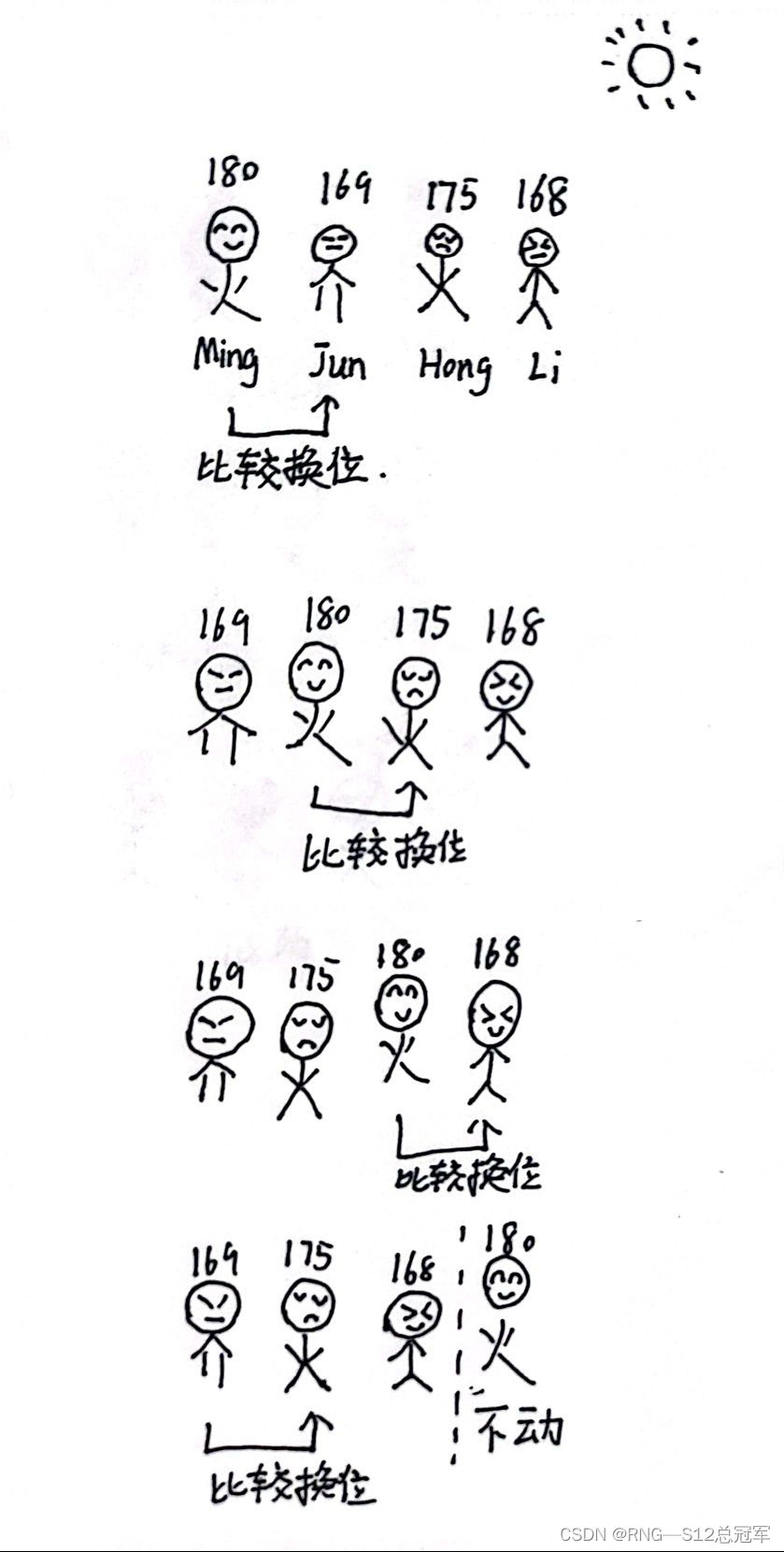
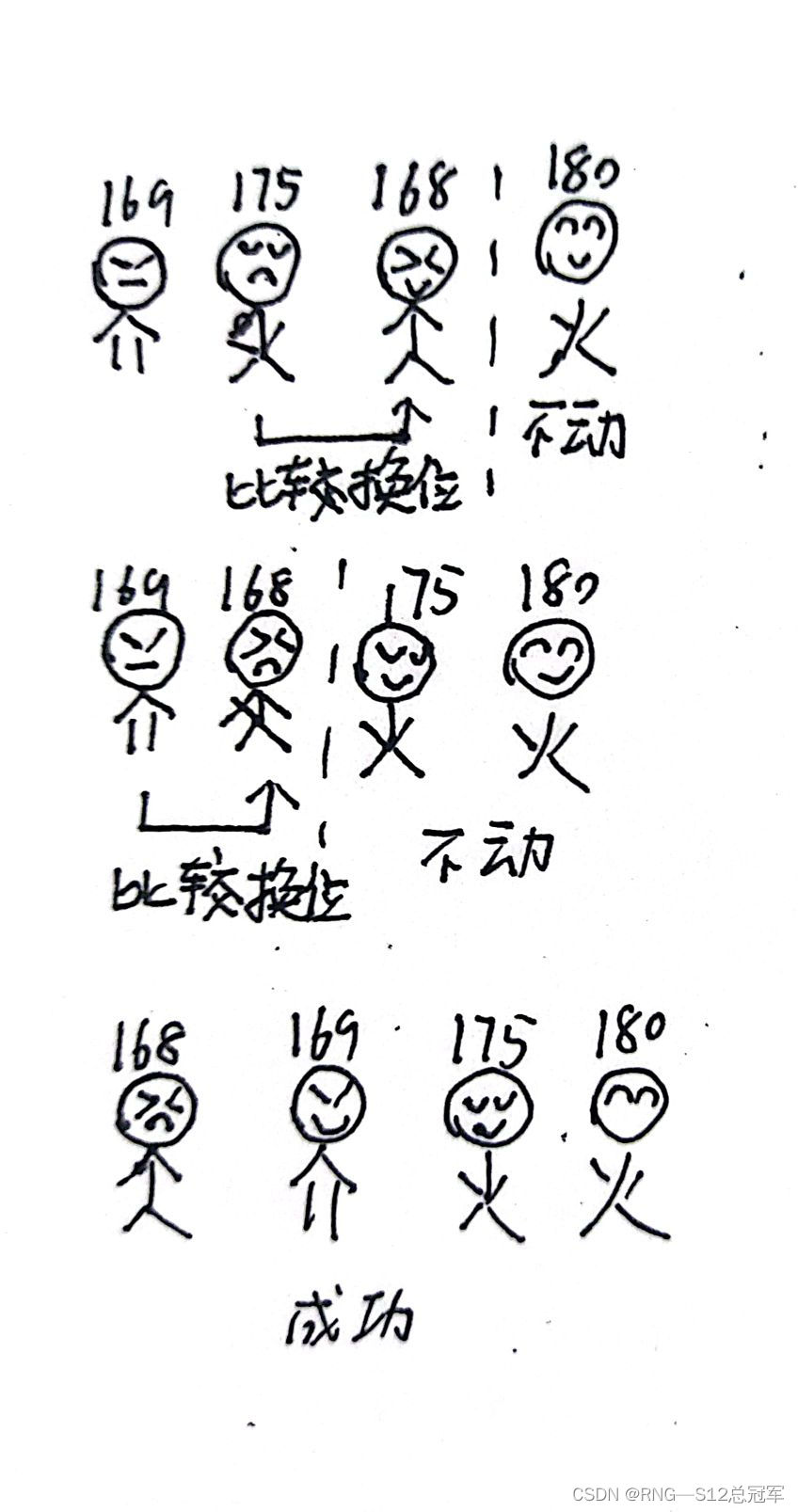
 有观察可知小明一共比较了3次，小军2次，小红1次（不换位，只比较）。比较数是依次递减的。所以我们容易想到使用循环的方法。

冒泡排序的代码实现：

要排序的数字已经存储在了数组arr中，

 for (int i = 0; i <arr.length-1; i++) {
            for (int j = 0; j < arr.length-i-1; j++) {
                 if(arr[j]>=arr[j+1]){
                    k=arr[j];
                    arr[j]=arr[j+1];
                    arr[j+1]=k;
                }
            }
        }

 思考三个问题：1，为什么i那里的arr.length要减1?

                   2，为什么j那里的arr,length要减1和 i ?

                   3，如果不引入 k 这个外来量那么数组能不能实现前后互换？

           

时间复杂度：

嵌套了两个循环，所以我们可以直接认为它是O(n²）。

如果严谨一点的话，我们可以通过数列求和的方法确定时间复杂度。还是小明等人的例子，小明一共比较了3次，小军2次，小红1次，所以是小明一共比较了n-1次，小军n-2次，小红n-3次。是一个等差数列，由等差数列求和公式可得：

 去掉低项式和系数之后就是O(n²)。

冒泡排序的优化：

刚刚所说的O(n²)是最大时间复杂度，而上面的代码的时间复杂度就是最大时间复杂度。

在实际生产中我们却不一定会遇到最大的时间复杂度，比如，180，168，169，175，这种的情况，其实在第一轮的排序中就已经完成了目标，时间复杂度为O(n)，但是如果使用上面的代码，他的时间复杂度就会是O(n²)。

据此请各位同学思考它的优化思路。