numpy前言矩阵（线性代数）

线性代数 矩阵

向量积np.dot

x=np.array([1,2])
y=np.array([3,4])
z=np.dot(x,y)
11
x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6], [7, 8]])
z=np.dot(x,y)
[[19 22]
 [43 50]]

注：在线性代数中的维数和数组中的不同，如线代中提到的n维行向量在 Numpy 中是一维数组，而线性代数中的n维列向量在 Numpy 中是一个shape为(n, 1)的二维数组

特征值与特征向量

np.linalg.eigvals(x)：计算特征值
np.linalg.eig(x)：计算特征值和特征向量，用两个参数去接收，前者保存特征值，后者保存特征向量

矩阵分解

• 奇异值分解
  u, s, v = numpy.linalg.svd(a, full_matrices=True, compute_uv=True, hermitian=False)
  a 是一个形如(M,N)矩阵
  full_matrices：默认取True，此时u为（M,M），v为（N,N），反之u为(M,K)，v为(K,N) ，K=min(M,N)
  compute_uv：默认取True 此时计算u,s,v 反之只计算s
  注：Numpy中返回的v是通常所谓奇异值分解a=usv’中v的转置

A = np.array([[4, 11, 14], [8, 7, -2]])
[[ 4 11 14]
 [ 8  7 -2]]
u,s,v=np.linalg.svd(A)
u:
[[ 0.9486833  -0.31622777]
 [ 0.31622777  0.9486833 ]]
 s:
 [18.97366596  9.48683298]
 v:
 [[ 0.33333333  0.66666667  0.66666667]
 [ 0.66666667  0.33333333 -0.66666667]
 [-0.66666667  0.66666667 -0.33333333]]

• QR分解
  np.linalg.qr(a, mode=‘reduced’)
  mode=‘reduced’：返回(M, N)的列向量两两正交的矩阵q，和(N, N)的三角阵r
  mode=‘complete’：返回(M, M)的正交矩阵q，和(M, N)的三角阵r

A = np.array([[1, 1], [1, -2], [2, 1]])
mode = reduced
q, r = np.linalg.qr(A, mode='reduced')
[[-0.40824829  0.34503278]
 [-0.40824829 -0.89708523]
 [-0.81649658  0.27602622]]
[[-2.44948974 -0.40824829]
 [ 0.          2.41522946]]
 np.dot(q,r)：
 [[ 1.  1.]
 [ 1. -2.]
 [ 2.  1.]]
 mode = complete
 q, r = np.linalg.qr(A, mode='complete')
 [[-0.40824829  0.34503278 -0.84515425]
 [-0.40824829 -0.89708523 -0.16903085]
 [-0.81649658  0.27602622  0.50709255]]
[[-2.44948974 -0.40824829]
 [ 0.          2.41522946]
 [ 0.          0.        ]]
 np.dot(q,r)：
 [[ 1.  1.]
 [ 1. -2.]
 [ 2.  1.]]

• Cholesky分解
  np.linalg.cholesky(a)
  返回正定矩阵a的 Cholesky 分解a = L*L.T，其中L是下三角

A = np.array([[1, 1, 1, 1], [1, 3, 3, 3],
              [1, 3, 5, 5], [1, 3, 5, 7]])
L = np.linalg.cholesky(A)
# [[1.         0.         0.         0.        ]
#  [1.         1.41421356 0.         0.        ]
#  [1.         1.41421356 1.41421356 0.        ]
#  [1.         1.41421356 1.41421356 1.41421356]]

范数

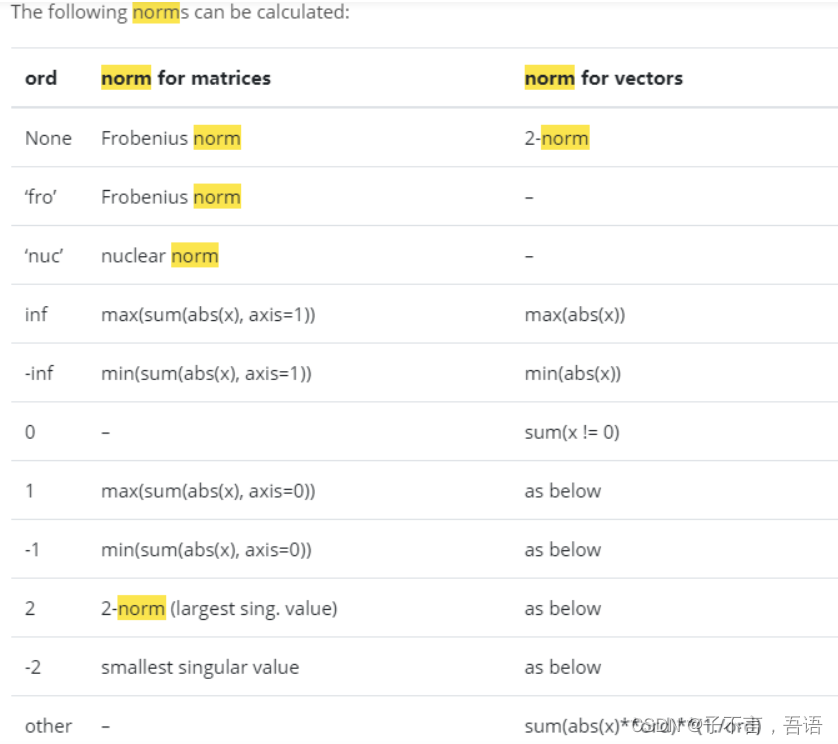
np.linalg.norm(x, ord=None, axis=None, keepdims=False)
计算向量或者矩阵的范数
根据ord参数的不同，计算不同的范数

行列式

np.linalg.det(x):计算行列式

秩与迹

np.linalg.matrix_rank()：矩阵的秩
np.trace()：矩阵的迹
方阵的迹就是主对角元素之和

逆矩阵与解方程

逆矩阵：
设 A 是数域上的一个 n 阶矩阵，若在相同数域上存在另一个 n 阶矩阵 B，使得：AB=BA=E（E 为单位矩阵），则我们称 B 是 A 的逆矩阵
np.linalg.inv():矩阵可逆的充要条件：det(a) != 0，或者a满秩

解线性方程组:
np.linalg.solve(a, b):求解线性方程组或矩阵方程