论文-Individual Fairness for Graph Neural Networks: A Ranking based Approach_individual fairness for local private graph neural-CSDN博客

本文链接：https://blog.csdn.net/qq_52968846/article/details/134276377

https://dl.acm.org/doi/abs/10.1145/3447548.3467266

注：仅作学习记录，欢迎指正

背景

群体公平：关注不同群体（由敏感属性划分）得到相似对待

个体公平：关注相似的人得到相似的对待（下图即Lipschitz mapping）

既往图神经网络的研究总是落在群体公平上。图数据是异构的，不同的数据模式（即图结构和节点属性）经常耦合在一起。因此，偏见和歧视可以以各种形式存在。在这方面，除了关于受保护属性的组公平性的概念之外，还希望深入研究图的原子组件（即节点），以确保图表示学习为相似的个体呈现相似的结果，从而实现个体公平。

解决问题

约束公式：由于输入空间和输出空间的距离度量差异，传统个体公平定义中利普希茨普常数通常很难指定。
距离校准：Lipschitz条件下的绝对距离比较无法校准不同实例之间的差异。（这里原文给了一个例子）
端到端的学习模式:GNN的节点嵌入是为了特定的下游学习任务定制的。如何将个体公平约束无缝地结合到学习过程中，而不危及其端到端的范式，是一个主要问题。

解决思路

REDRESS（Ranking basEd inDividual faiRnESS的简称）

为了应对前两个挑战，从排名的角度细化了个人公平的定义：“针对每个实例𝑢𝑖 , 其他实例在输入空间和结果空间的两个排名列表（基于它们到𝑢𝑖的距离) 应该尽可能相似”。避免两个不同距离度量之间的精细距离比较，相对排名比较也可以自然地缓解未校准距离的问题。
为了应对第三个挑战，REDRESS中封装了两个优化模块，分别提高模型效用和个体公平性。为了适应端到端的训练过程，对两个优化模块进行了设计，以适应基于梯度的优化技术。

REDRESS

GNN backbone+Utility Maximization+Individual fairness optimization

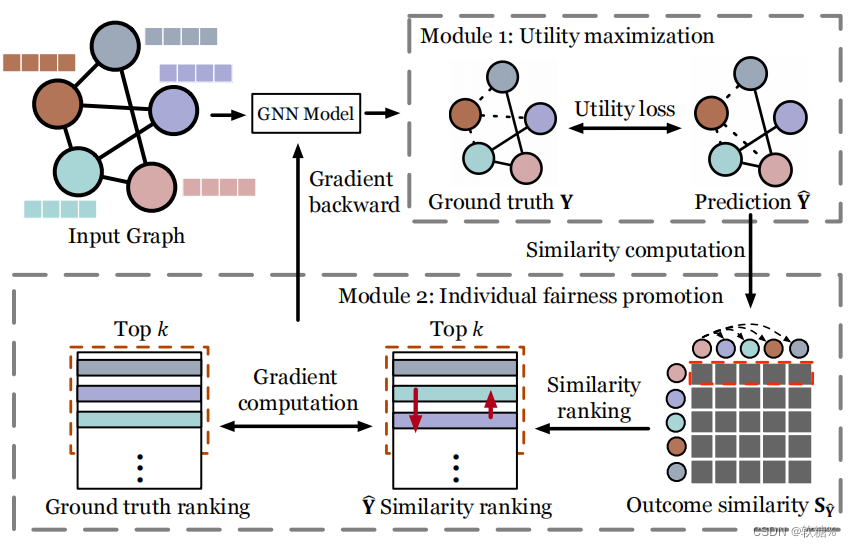
1. GNN backbone model

$l+1$ 层的输出： $h_{v}^{(l+1)}=\sigma (combine(h_{v}^{(l)},f(\{h_{u}^{(l)}\}) )),u\in N(v)$

其中：combine表示二者结合，u是v的邻居节点， $\sigma$ 是激活函数（例：ReLU）

将最后一个GNN层的输出表示为矩阵Z∈ $R^{n\times c}$ , 则可以获得GNN的预测，即softmax（Z）∈ $R^{n\times c}$ 用于节点分类和sigmoid（ $Z^{T}Z$ ）∈ $R^{n\times n}$ 用于链接预测.

2. Utility Maximization

效用最大化可以通过最小化损失函数来实现。

损失函数： $L_{utility} =-\sum_{(i,j)\in L}Y_{ij}ln\widehat{Y}_{ij}$

其中：L是节点分类中训练节点的（节点，类）元组集，链接预测中训练边的（节点，节点）元组集。

对于前面的问题3，由于损失函数相对于模型参数是可微分的，基于梯度的优化技术可以直接应用于端到端训练。

3.Individual fairness optimization

一个直接解决方案：

从每个节点的Oracle相似矩阵 $S_{G}$ 和输出相似矩阵 $S_{\widehat{Y}}$ 导出两个排名列表，然后定义一个损失函数来量化这两个排行列表之间的差异。之后，我们可以将所有节点上的损失函数组合在一起，并最大限度地减少总体损失，以获得可以促进个体公平性的更好的 $\widehat{Y}$ 。

但是，由于排序列表的排序操作将使总损失函数不再可微分（相对于GNN模型参数），在某种程度上，基于梯度的优化技术无法直接应用。因此，提出下面的解决方案。

“比起m，i更相似于j”的可能性得分定义为：

在输出相似矩阵 $S_{\widehat{Y}}$ 中：

在oracle相似矩阵 $S_{G}$ 中：

采用一种基于概率的损失函数。节点对（ $u_{j}$ , $u_{m}$ ）以 $u_{i}$ 为中心的交叉熵损失函数定义为：

$L_{j,m}(i)= -P_{j,m}log\widehat{P}_{j,m} -(1-P_{j,m})log(1-\widehat{P}_{j,m})$

于是所有节点对以 $u_{i}$ 为中心的损失函数为

$L_{fairness} =\sum_{(j,m)}L_{j,m}(i)$

在有众多节点的网络中，这通常很难实现，下面考虑训练优化。

定义 $Z_{@k} (\cdot ,\cdot )$ 作为每个节点的 $S_{G}$ 和 $S_{\widehat{Y}}$ 得出的top-k ranking list之间的相似性度量。

于是节点 $u_{i}$ 的损失函数重新定义为

$L_{fairness}(i) =\sum_{(j,m)}L_{j,m}(i)\left | \Delta Z_{@k} \right |_{j,m}$

当 $u_{j}$ ， $u_{m}$ 都不是来自 $S_{\widehat{Y}}$ 的top-k节点， $|\Delta Z_{@k} |_{j,m}$ 为0；

否则， $| \Delta Z_{@k} |_{j,m}=|Z_{@k}(list_{u_{i}},\widehat{list}_{u_{i}})-Z_{@k}(list_{u_{i}},\widehat{list}_{u_{i}}^{'})|$ ,其中 $\widehat{list}_{u_{i}}^{'}$ 交换了 $\widehat{list}_{u_{i}}$ 中 $u_{j}$ 和 $u_{m}$ 的位置。

为了进一步优化，可以直接限制 $u_{j}$ ， $u_{m}$ 都是来自 $S_{\widehat{Y}}$ 的top-k节点。

损失函数： $L_{total}=L_{utility}+\gamma L_{fairness}$

实验

在节点分类和链接预测任务下分别进行了几个实验，采用了各种GNN backbone。

探求了以下三个问题：

在效用和个人公平方向的表现如何？
优于目前的先进方案
$\gamma$ 的选择有什么影响？
$\gamma$ 较小时，和NDCG@10在效用和公平性表现相当；
$\gamma$ 适中时，在不影响效用的情况下改善了个体公平性；
$\gamma$ 过大时，效用受到影响，个体公平性的效果也随着 $\gamma$ 的增大而更差。
$k$ 的选择有什么影响？
$k$ 增大时，个体公平性效果越好，效用几乎不受影响。