用于图像识别的判别图正则化技术

本文链接：https://blog.csdn.net/qq_53123067/article/details/141200263

在数字图像的世界里，我们每天都被无数视觉信息包围着——从智能手机的照片到自动驾驶汽车的实时视频流，这些图像不仅记录了我们的生活，还塑造了我们对世界的理解。然而，在这些图像背后，隐藏着一种强大的计算技术，使得计算机能够“看见”和“理解”这些视觉数据。这就是图像识别技术的魅力所在。而在这一领域，如何提高算法的准确性和鲁棒性，一直是研究者们的核心挑战之一。

概述

宽度学习系统 (BLS) 被提出作为深度学习的一种替代方法。 BLS 的架构是将输入随机映射到一系列形成特征节点的特征空间中，然后将特征节点的输出广泛扩展形成增强节点，然后可以通过分析确定网络的输出权重。 BLS 的最大优势是当出现新的输入数据或神经元节点时，可以增量学习而无需重新训练过程。已经证明 BLS 能够克服基于梯度的深度学习算法中训练大量参数所带来的不足。在论文中，作者们提出了一种新颖的判别图正则化宽度学习系统 (GBLS)。考虑到数据的局部不变性属性，这意味着相似的图像可能具有相似的属性，流形学习被纳入到标准 BLS 的目标函数中。在 GBLS 中，输出权重受到限制以学习更具有辨别信息，分类能力可以进一步增强。进行了多项实验证明我们提出的 GBLS 模型可以胜过标准 BLS。

这里我们参考了论文：地址，在这篇论文中，作者的主要工作是对BLS进行了改进创新，但其中为BLS的目标函数设计的判别图正则化技术在我们了解其原理之后可以应用到各种图像识别领域的模型中去，对于我们进一步改善模型的判别性和提升模型效率有着很大的帮助：

随着人工智能技术的持续进步，图学习已经引起了许多研究人员的关注。通常，通过构建图和图匹配，图学习方法获取数据中的拓扑结构和潜在信息。图匹配的目标是找到两个图之间的结构相似性，这可以帮助我们理解复杂的图数据。例如，林一洁等人提出了一种名为对比匹配的动量蒸馏的新方法，可以更好地探索节点之间和边之间的相关性。此外，图构建将原始数据转换为图结构，用于后续的图分析和图学习任务。基于此，彭曦等人通过构建一种名为 L2-图的稀疏相似性图提出了稳健的子空间聚类和子空间学习算法。此外，为了挖掘数据中的潜在信息，研究人员已经将图构建与 BLS 结合起来。通过构建数据的内在图，图正则化广义学习系统（GBLS）在训练过程中考虑了数据的内在关系。根据构建的图，可以将适当的图正则化项嵌入标准 BLS 的目标函数中，从而提高 BLS 的学习能力。

算法流程

在标准BLS中嵌入判别图正则化的方法，首先，假设存在输入数据集{X,Y}{X,Y}。考虑到相同类型的数据来自同一流形空间，不同类型的数据来自不同的流形空间，我们通过(8)构建图VV，图VV是相似性矩阵，代表了图顶点之间的关系。

其中 NtNt 代表 tt 类样本的数量，l(⋅)l(⋅) 代表样本的标签。通过这种方式，我们能够考虑数据的流形结构。我们可以利用图 VV 获取图正则项 EGEG 。

其中 yiyi，yjyj 分别代表 xixi 和 xjxj 的预测值，LGLG 则是图拉普拉斯矩阵，关于宽度学习系统，我在前面提到过输入数据将被映射成一次和二次特征，我们叫做特征节点和增强节点，在这里为了得到图正则项，我们需要根据这部分节点层得到一个先验的预测结果Y^Y^，计算方法可通过公式 (3) , WW 是随机初始化的权重矩阵。

接下来获得图正则化项 LGLG 后，我们可以更新原始BLS的目标函数 (4) 得到新的目标函数 (5)。

通过上述公式计算 WW 的偏导数，并最终可以通过公式(6)计算 WW :

从上面可以看出，GBLS考虑了数据的基本几何结构，而标准BLS忽视了这一点，这是通过在(4)中添加一个常规图项来实现的。因此，输出权重可以受限以学习更具有区分性的信息，进一步增强分类能力。

接下来我讲解一下，在加入了判别图正则化后，宽度模型的整体架构会如何变化。我将从输入数据开始到最终输出预测结果详细地介绍模型如何处理数据及内部的特征。

如上所述，与标准 BLS 相比，GBLS 添加了图形正则项以考虑数据之间的内在关系，与此同时，GBLS 像 BLS 一样，使用传统的稀疏自编码器来微调获得的特征。具体的实施步骤如下：

给定数据集 {X,Y}{X,Y}，我们首先随机生成一个权重矩阵 WW，将 XX 转换为映射特征节点 ZZ，然后通过稀疏自编码器算法 fSA(X,Z)fSA(X,Z) 获得所需的权重 W^TW^T。通过 W^TW^T，我们可以将原始数据 XX 转换为我们想要的 nn 组映射特征节点层 ZZ。

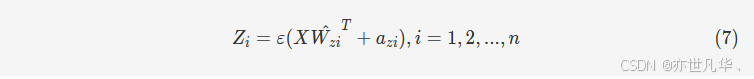
其中 Wz^T=fSA(X,Z)Wz^T=fSA(X,Z)，ε(⋅)ε(⋅) 是非线性激活函数，aziazi 是随机生成的偏置项，因此映射特征层可以定义为 Zn=[Z1,Z2,...,Zn]Zn=[Z1,Z2,...,Zn]，通过公式(8)可以得到增强节点层 HH。

ψ(⋅)也是一个非线性激活函数，而 $\beta _ { Hj } $ 和 $ \hat { W_ { Hj } }$ 分别是随机生成的偏置项和权重。这样，我们可以通过合并映射特征和网络的增强节点 BB 来获得输入层。B=[Zn∣Hm]B=[Zn∣Hm],接下来，我们需要计算连接系数 WW，使得 Y=BWY=BW。对于数据集 X,YX,Y，通过构建数据的内在图(通过(1)和(2) )，我们可以获得图正则项 EG=Tr(YT^LGY^)EG=Tr(YT^LGY^)。值得注意的是，这里 Y^Y^ 是新获得的输入层 BB 的预测结果。因此，获得 WW 的优化问题可以被定义为

通过计算 WW 的偏导数，可以得到 WW 由下式得到

代码复现

为了完整复现GBLS的算法流程，我使用层次化结构在五个文件中实现了模型的不同侧面。分别是bls2deep_graph.py文件——用于实现模型的整体架构、generateLmatrix.py文件——用于构建图拉普拉斯矩阵、GBLS.py文件——顶层文件用于端到端实现、sparse_bls_autoencoder.py文件——用于稀疏自编码器微调机制的实现、util.py文件——实用方法的集成，下面我将对算法的核心部分generateLmatrix.py文件、bls2deep_graph.py文件和GBLS.py文件分别给出他们的伪代码流程图并进行讲解，具体的代码可见附件，图拉普拉斯矩阵的构建——generateLmatrix.py文件：

函数 generateLmatrix(train_x, train_y, opt):
    # 获取标签
    gnd = 调用 result_tra(train_y)
    Label = 获取 gnd 的唯一值
    nLabel = Label 的数量
    nSmp = train_x 的行数

    # 初始化权重矩阵 A
    A = 创建一个 nSmp x nSmp 的零矩阵

    # 遍历每个标签
    对于每个标签 Label[idx]:
        classIdx = gnd == Label[idx]
        设置 A 中 classIdx 对应元素为 1 / classIdx 的和

    # 减去 A 的对角线元素
    A = A - A 的对角线元素

    # 计算度矩阵 D
    D = A 每行的和

    # 计算拉普拉斯矩阵 L
    如果 opt['NORMALIZE'] == 1:
        D_inv_sqrt = D 的逆平方根对角矩阵
        L = 单位矩阵 - D_inv_sqrt * A * D_inv_sqrt
    否则:
        L = D 的对角矩阵 - A

    返回 L

这段代码的主要功能是生成一个拉普拉斯矩阵，该矩阵常用于图形或网络分析中，帮助理解数据之间的关系。首先通过 result_tra 函数获取标签 gnd 并通过 np.unique 获取唯一标签 Label。然后创建一个大小为 nSmp x nSmp 的零矩阵 A，其中 nSmp 是样本数。接下来，遍历每个唯一标签 Label[idx]，找到属于当前标签的样本索引 classIdx，并将权重矩阵 A 中对应于 classIdx 的元素设为 1 / 当前标签的样本数。随后，将权重矩阵 A 的对角线元素置为零。计算度矩阵 D，D 是权重矩阵 A 每行元素的和。如果选项 opt['NORMALIZE'] 为 1，则计算归一化拉普拉斯矩阵 L，否则计算非归一化拉普拉斯矩阵 L，最后返回计算好的拉普拉斯矩阵 L。

复现模型整体架构——bls2deep_graph.py文件，这段代码的功能主要是实现了GBLS的训练和测试过程。首先对输入数据进行预处理，然后通过特征映射层和增强层对数据进行特征提取和增强。特征映射层通过多个随机权重窗口来生成特征，而增强层则使用正交随机权重进行特征增强。随后，代码计算输出权重并通过伪逆矩阵求解。最后，代码对训练和测试数据分别计算输出并评估准确率。整个过程包括数据预处理、特征映射、增强层训练、输出层训练和测试阶段：

函数 bls2deep_graph(train_x, train_y, test_x, test_y, N1, N2, N3, L, s, c):
    标准化 train_x
    添加偏置项到 train_x，生成 FeatureOfInputDataWithBias
    初始化 OutputOfFeatureMappingLayer 和相关变量

    记录开始时间 time_start

    对于 i 从 0 到 N2-1:
        生成权重矩阵 weightOfEachWindow
        计算特征映射 FeatureOfEachWindow
        缩放特征映射到 [-1, 1]
        计算 betaOfEachWindow 并保存
        计算输出 outputOfEachWindow 并缩放，保存到 OutputOfFeatureMappingLayer

    添加偏置项到 OutputOfFeatureMappingLayer，生成 InputOfEnhanceLayerWithBias

    生成增强层权重 weightOfEnhanceLayer 并计算增强层输出 OutputOfEnhanceLayer
    计算伪逆矩阵 pinvOfInput 并计算输出权重 OutputWeight

    记录结束时间 time_end，计算训练时间 trainTime
    计算训练集上的输出 OutputOfTrain 和准确率 trainAcc

    标准化 test_x 并添加偏置项，生成 FeatureOfInputDataWithBiasTest
    初始化 OutputOfFeatureMappingLayerTest

    记录开始时间 time_start

    对于 i 从 0 到 N2-1:
        计算每个窗口的测试输出 outputOfEachWindowTest 并缩放，保存到 OutputOfFeatureMappingLayerTest

    添加偏置项到 OutputOfFeatureMappingLayerTest，生成 InputOfEnhanceLayerWithBiasTest
    计算增强层测试输出 OutputOfEnhanceLayerTest

    拼接生成 InputOfOutputLayerTest，计算测试集上的输出 OutputOfTest

    记录结束时间 time_end，计算测试时间 testTime 和测试集上的准确率 testAcc

    返回 testAcc 和 trainAcc

这段代码的功能是实现数据预处理、生成拉普拉斯矩阵并训练和测试GBLS模型。首先，通过定义 preprocess_data 函数加载并返回训练和测试数据，从 ./ORL/ORL7.mat 文件中加载训练数据 train_x、测试数据 test_x、训练标签 train_y 和测试标签 test_y，然后调用 check_inf_nan 函数检查数据中是否有无穷大或 NaN 值。接着，调用 generateLmatrix 函数，基于训练数据和标签生成拉普拉斯矩阵 L，并打印生成的拉普拉斯矩阵的形状。之后，定义模型的超参数，包括正则化参数 C、收缩参数 s 以及其他参数 par，NumWin 表示窗口数量，NumWinNode 表示每个窗口的节点数量，NumHid 表示隐藏层节点数量。最后，调用 bls2deep_graph 函数，传入训练和测试数据、拉普拉斯矩阵和其他超参数，训练并测试基于 BLS 的模型，最终输出训练准确率 trAcc 和测试准确率 ttAcc。总结来说，这段代码的主要功能是加载和预处理数据，生成拉普拉斯矩阵，并使用深度广度学习系统（BLS）进行模型训练和测试，最终输出训练和测试的准确率。

函数 preprocess_data():
    加载并预处理数据
    返回 train_x, test_x, train_y, test_y

#加载数据:
    调用 preprocess_data 函数，获取 train_x, test_x, train_y, test_y
    检查 train_x 中是否有无穷大或 NaN 值

#处理测试集:
    随机排列 test_x 的行顺序
    设置 opt 字典，NORMALIZE 为 1
    打印 train_x, train_y, test_x, test_y 的形状

#生成拉普拉斯矩阵:
    调用 generateLmatrix 函数，传入 train_x, train_y, opt，得到 L
    打印 L 的形状

#设置参数:
    C = 2 ** -30
    s = 0.8
    par 字典，包含 lambdaG, C, s, NumLayer, range, randstate, ActFun

#设置模型参数:
    NumWin = 10
    NumWinNode = 20
    NumHid = 100

#训练和测试模型:
    调用 bls2deep_graph 函数，传入 train_x, train_y, test_x, test_y, NumWin, NumWinNode, NumHid, L, s, C
    获取并返回训练和测试准确率 trAcc, ttAcc

接下来运行代码便可以进行模型的训练和测试，最后我们需要输出对模型预测的评价指标，常见的对分类任务的评价指标有准确度，F1分数和查准率等，在这里我已经在bls2deep_graph.py的show_accuracy函数中为大家实现了一些通用的评价指标，大家也可以根据自己的需要编写更对的评价指标计算方法对模型进行更多方面的评估，得到输出结果，这里以ORL6数据集为例，调整模型节点数为10，200，100：

在原论文中，作者将GBLS模型在多个图像识别数据集上进行了实验以验证了他们算法的有效性，因此，我在同样的的三种经典图像识别数据集上进行了多次实验，一是向大家介绍该如何使用这份代码，二是验证了这份代码的可靠性。实验结果如下图所示：

可以看到搭建的模型在三份数据集上都能取得不错而且稳定的效果，在粗略的手调情况下，在三份数据集上的各项指标都能达到90%以上，在UMIST数据集上的效果甚至已经达到原论文数值。同时，可以看到我们在一定范围内调节网络的节点数模型的分类效果保持稳定，在网络结构拓宽时分类性能稳步提升，这说明了搭建的模型学习能力不会出现剧烈抖动，我们可以通过网格搜索来进一步寻找到能让模型收敛的最优参数。

写在最后

经过对判别图正则化技术的深入探讨，我们可以看到，这一创新方法不仅为图像识别领域带来了新的突破，也揭示了计算机视觉中的复杂动态和潜力。通过在图像识别模型中引入判别图正则化，我们不仅优化了模型的分类性能，更提升了其在复杂环境中的鲁棒性。它巧妙地利用了数据的结构信息，使得模型能够在面对噪声和变异时仍保持高效准确的表现。

但这仅仅是开始。随着技术的不断进步和应用领域的不断扩展，判别图正则化技术可能会在未来发挥更大的作用。从医疗影像分析到自动驾驶，甚至到我们日常生活中的智能设备，这项技术的潜力几乎是无限的。它不仅推动了图像识别技术的前沿发展，也为我们揭示了智能系统如何以更精细、更智能的方式理解和解释世界。

在展望未来时，我们不禁要思考：随着算法的不断优化和计算能力的提升，判别图正则化技术将如何进一步演变？它会如何影响我们生活的各个方面，并为未来的技术创新提供新的动力？这些问题值得我们每一个研究者、工程师以及技术爱好者继续探索和思考。

详细复现过程的项目源码、数据和预训练好的模型可从地址获取。