什么是回溯法?
回溯法(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
用回溯算法解决问题的一般步骤:
1、 针对所给问题,定义问题的解空间,它至少包含问题的一个(最优)解。
2 、确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间 。
3 、以深度优先的方式搜索解空间,并且在搜索过程中用剪枝函数避免无效搜索。
基本思想
从一条路往前走,能进则进,不能进则退回来,换一条路再试。
能解决哪些问题?
- 排列、组合(子集、幂集、字符全排列)。
-
二维数组下的DFS搜索(黄金矿工、数独、装载问题、0-1背包问题、旅行售货员问题、八皇后问题、迷宫问题、图的m着色问题)
- 数组、字符串,给定一个特定的规则,尝试搜索迭代找到某个解。
回溯的解空间
回溯算法有两种常见的解空间模型,分别对应数学中的两种暴力思想,组合以及排列。其中子集问题,对应数学中的组合问题。排列问题对应数学中的排列问题。
解数独
数独,是源自18世纪瑞士的一种数学游戏。是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫(3*3)内的数字均含1-9,不重复。
数独盘面是个九宫,每一宫又分为九个小格。在这八十一格中给出一定的已知数字和解题条件,利用逻辑和推理,在其他的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次,所以又称“九宫格”

利用回溯算法解数独。思路如下:
1,从0行0列开始,依次往里面填入1-9的数字;
2,然后判断填入这个数字后,该数字对应的行,列和九宫格是否满足不重复的条件;
3,如果当前填入的数字满足,就继续填入下一个数字,下一个数字又从1-9中尝试,如果有满足的数字就说明该数字可用,如果没有,则将该数字又重新置为空格,如此循环往复;
4,如果将所有的数字都尝试了还是没有合适的额,那说明本问题无解,返回false;
/*
*java 递归
*/
public class ShuduPro {
private int[][] sudoku;
public ShuduPro(int[][] sudoku) {
this.sudoku = sudoku;
}
public static void main(String[] args) {
int[][] sudoku={
{7, 0, 0, 0, 0, 0, 0, 0, 9},
{1, 4, 0, 3, 0, 9, 0, 0, 6},
{0, 0, 0, 0, 0, 0, 5, 1, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 2, 0, 8, 1, 0, 0, 0},
{0, 0, 9, 0, 2, 0, 8, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 2, 8, 5, 0, 6, 9, 0, 0},
{0, 0, 0, 1, 0, 0, 3, 0, 2}
};
ShuduPro sudu = new ShuduPro(sudoku);
sudu.backTrace(0,0);
}
private void backTrace(int i, int j) {
//完成,打印数组
if(i==8 && j==9){
print_sudoku();
return;
}
//判断是否到列尾,到列尾没到行尾,就换行
if(j == 9){
i++;
j=0;
}
//如果是空格就填值
if (sudoku[i][j] == 0){
for (int n = 1; n <=9; n++){
//判断空格中填任一个数是否符合规则
if(check_repeat(i,j,n)){
/*
*赋值
* 进入下一个空格
* 初始化该空格
*/
sudoku[i][j] = n;
backTrace(i,j+1);
sudoku[i][j]=0;
}
}
}else{
backTrace(i,j+1);
}
}
/**
*
* @param row 行号
* @param col 列号
* @param temp 赋的值
* @return
*/
private boolean check_repeat(int row, int col, int temp) {
//判断所在行和列是否有重复数字
for (int i=0; i < 9; i++){
if(sudoku[row][i] == temp || sudoku[i][col] == temp){
return false;
}
}
//判断所在小九宫格中是否有重复
int tempRow = (row / 3) * 3;
int tempCol = (col / 3) * 3;
for (int i = 0; i < 3; i++){
for (int j = 0; j < 3; j++){
if(sudoku[tempRow + i][tempCol + j] == temp){
return false;
}
}
}
return true;
}
//打印矩阵
private void print_sudoku() {
for (int i = 0; i < 9; i++){
for (int j = 0; j < 9; j++){
System.out.print(sudoku[i][j]+" ");
}
System.out.println(" ");
}
System.out.println(" ");
}
}
数独结果:
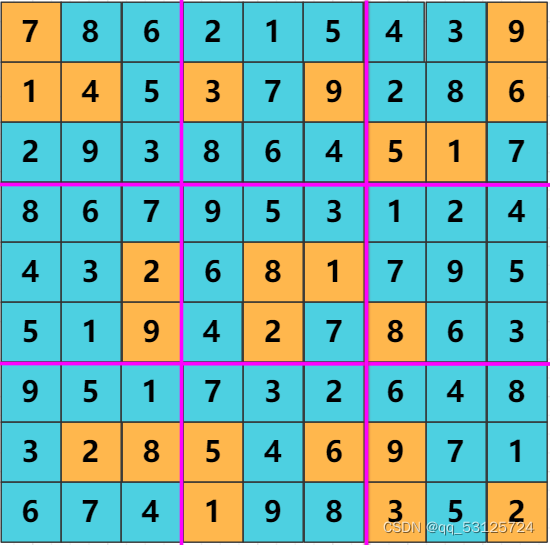
























 3619
3619

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








