CVPR2022暗光增强算法SCI理解＋复现-CSDN博客

本文链接：https://blog.csdn.net/qq_53388162/article/details/147747852

一.相关资料

论文地址：[2204.10137] Toward Fast, Flexible, and Robust Low-Light Image Enhancement
SCI源码：https://github.com/vis-opt-group/SCI

二.sci简介

现有的弱光图像增强技术不仅难以兼顾视觉质量和计算效率，而且在未知的复杂场景下往往失效。本文提出了一种新的自校准光照（SCI）学习框架，用于在真实的弱光环境中快速、灵活、鲁棒地对图像进行增亮处理.具体地说，我们建立了一个具有权重共享的级联光照学习过程来处理这个任务。考虑到级联模式的计算量，我们构造了自校准模块，实现了各级结果的收敛，产生了仅使用单个基本块进行推理的增益（在以前的工作中还没有开发过），从而大大降低了计算量。然后定义了无监督训练损失，以提高模型适应一般场景的能力。在此基础上，对SCI的内在特性（现有研究中所缺乏的），包括操作不敏感的

适应性（在不同通讯作者的背景下获得稳定的表现）进行了全面的探索。很少的简单操作）和与模型无关的通用性（可应用于基于照明的现有工作以提高性能）。最后，大量的实验和烧蚀研究充分表明了我们在质量和效率上的优越性。在微光人脸检测和夜间语义分割等方面的应用充分展示了SCI潜在的实用价值。

上面是论文中的摘要，总结一下特点：1.无监督学习（不需要成对的图片训练） 2.轻量级（速度很快）

三.主要贡献

1.考虑到级联模式的计算量，我们构造了自校准模块，实现了各级结果的收敛，产生了仅使用单个基本块进行推理的增益。（结构新，后面结合代码解释）

2.定义了无监督训练损失，以提高模型适应一般场景的能力。

四.SCI网络结构

整个网络由校准网络和增强网络构成

1.权重共享照明学习（代码中EhanceNetwork）

看看代码：

class EnhanceNetwork(nn.Module):
    def __init__(self, layers, channels):
        super(EnhanceNetwork, self).__init__()
 
        kernel_size = 3
        dilation = 1
        padding = int((kernel_size - 1) / 2) * dilation
 
        self.in_conv = nn.Sequential(
            nn.Conv2d(in_channels=3, out_channels=channels, kernel_size=kernel_size, stride=1, padding=padding),
            nn.ReLU()
        )
 
        self.conv = nn.Sequential(
            nn.Conv2d(in_channels=channels, out_channels=channels, kernel_size=kernel_size, stride=1, padding=padding),
            nn.BatchNorm2d(channels),
            nn.ReLU()
        )
 
        self.blocks = nn.ModuleList()
        for i in range(layers):
            self.blocks.append(self.conv)
 
        self.out_conv = nn.Sequential(
            nn.Conv2d(in_channels=channels, out_channels=3, kernel_size=3, stride=1, padding=1),
            nn.Sigmoid()
        )
 
    def forward(self, input):
        fea = self.in_conv(input)
        for conv in self.blocks:
            fea = fea + conv(fea)
        fea = self.out_conv(fea)
 
        illu = fea + input
        illu = torch.clamp(illu, 0.0001, 1)
 
        return illu

这个网络很精炼，简单的残差结构，普通的卷积操作，以最精炼的结构提取更多的特征，Sigmoid()限制输出范围（0-1），看完代码大家可能有一个疑问，并没有体现它的阶段性，公式中的t阶段在哪里呢？别急，我们继续往下看。

2.自校准模块（代码中CalibrateNetwork）

同样也是看看代码：

class CalibrateNetwork(nn.Module):
    def __init__(self, layers, channels):
        super(CalibrateNetwork, self).__init__()
        kernel_size = 3
        dilation = 1
        padding = int((kernel_size - 1) / 2) * dilation
        self.layers = layers
 
        self.in_conv = nn.Sequential(
            nn.Conv2d(in_channels=3, out_channels=channels, kernel_size=kernel_size, stride=1, padding=padding),
            nn.BatchNorm2d(channels),
            nn.ReLU()
        )
 
        self.convs = nn.Sequential(
            nn.Conv2d(in_channels=channels, out_channels=channels, kernel_size=kernel_size, stride=1, padding=padding),
            nn.BatchNorm2d(channels),
            nn.ReLU(),
            nn.Conv2d(in_channels=channels, out_channels=channels, kernel_size=kernel_size, stride=1, padding=padding),
            nn.BatchNorm2d(channels),
            nn.ReLU()
        )
        self.blocks = nn.ModuleList()
        for i in range(layers):
            self.blocks.append(self.convs)
 
        self.out_conv = nn.Sequential(
            nn.Conv2d(in_channels=channels, out_channels=3, kernel_size=3, stride=1, padding=1),
            nn.Sigmoid()
        )
 
    def forward(self, input):
        fea = self.in_conv(input)
        for conv in self.blocks:
            fea = fea + conv(fea)
 
        fea = self.out_conv(fea)
        delta = input - fea
 
        return delta

网络同样很精炼，简单的残差结构，普通的卷积操作，比上个模块多一层卷积和归一化，

nn.Conv2d(in_channels=channels, out_channels=channels, kernel_size=kernel_size, stride=1, padding=padding),
nn.BatchNorm2d(channels),

以最精炼的结构提取更多的特征，Sigmoid()限制输出范围（0-1），同样公式中的t阶段在哪里呢？别急，我们继续往下看。

3.总体网络

class Network(nn.Module):
 
    def __init__(self, stage=3):
        super(Network, self).__init__()
        self.stage = stage
        self.enhance = EnhanceNetwork(layers=1, channels=3)
        self.calibrate = CalibrateNetwork(layers=3, channels=16)
        self._criterion = LossFunction()
 
    def weights_init(self, m):
        if isinstance(m, nn.Conv2d):
            m.weight.data.normal_(0, 0.02)
            m.bias.data.zero_()
 
        if isinstance(m, nn.BatchNorm2d):
            m.weight.data.normal_(1., 0.02)
 
    def forward(self, input):
 
        ilist, rlist, inlist, attlist = [], [], [], []
        input_op = input
        for i in range(self.stage):
            inlist.append(input_op)
            i = self.enhance(input_op)
            r = input / i
            r = torch.clamp(r, 0, 1)
            att = self.calibrate(r)
            input_op = input + att
            ilist.append(i)
            rlist.append(r)
            attlist.append(torch.abs(att))
 
        return ilist, rlist, inlist, attlist
 
    def _loss(self, input):
        i_list, en_list, in_list, _ = self(input)
        loss = 0
        for i in range(self.stage):
            loss += self._criterion(in_list[i], i_list[i])
        return loss

这里我们注意stage=3，这里就是对应的阶段，源代码中为3，也就是将网络重复三次。这里还可以发现上一阶段的EhanceNetwork的结果与当前阶段的结果的比值为CalibrateNetwork的输入，用比值去校准。

4.损失函数（无监督损失训练）

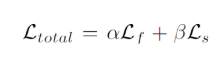
Lf ：表示保真度；Ls ：表示平滑损失

（1）保真度

上程序：

Fidelity_Loss = self.l2_loss(illu, input)

就是MSE损失目的每个阶段输入之间的像素级一致性，防止图片失去原有纹理。

（2）平滑损失

上代码：


class SmoothLoss(nn.Module):
    def __init__(self):
        super(SmoothLoss, self).__init__()
        self.sigma = 10
 
    def rgb2yCbCr(self, input_im):
        im_flat = input_im.contiguous().view(-1, 3).float()
        mat = torch.Tensor([[0.257, -0.148, 0.439], [0.564, -0.291, -0.368], [0.098, 0.439, -0.071]]).cuda()
        bias = torch.Tensor([16.0 / 255.0, 128.0 / 255.0, 128.0 / 255.0]).cuda()
        temp = im_flat.mm(mat) + bias
        out = temp.view(input_im.shape[0], 3, input_im.shape[2], input_im.shape[3])
        return out
 
    # output: output      input:input
    def forward(self, input, output):
        self.output = output
        self.input = self.rgb2yCbCr(input)
        sigma_color = -1.0 / (2 * self.sigma * self.sigma)
        w1 = torch.exp(torch.sum(torch.pow(self.input[:, :, 1:, :] - self.input[:, :, :-1, :], 2), dim=1,
                                 keepdim=True) * sigma_color)
        w2 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-1, :] - self.input[:, :, 1:, :], 2), dim=1,
                                 keepdim=True) * sigma_color)
        w3 = torch.exp(torch.sum(torch.pow(self.input[:, :, :, 1:] - self.input[:, :, :, :-1], 2), dim=1,
                                 keepdim=True) * sigma_color)
        w4 = torch.exp(torch.sum(torch.pow(self.input[:, :, :, :-1] - self.input[:, :, :, 1:], 2), dim=1,
                                 keepdim=True) * sigma_color)
        w5 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-1, :-1] - self.input[:, :, 1:, 1:], 2), dim=1,
                                 keepdim=True) * sigma_color)
        w6 = torch.exp(torch.sum(torch.pow(self.input[:, :, 1:, 1:] - self.input[:, :, :-1, :-1], 2), dim=1,
                                 keepdim=True) * sigma_color)
        w7 = torch.exp(torch.sum(torch.pow(self.input[:, :, 1:, :-1] - self.input[:, :, :-1, 1:], 2), dim=1,
                                 keepdim=True) * sigma_color)
        w8 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-1, 1:] - self.input[:, :, 1:, :-1], 2), dim=1,
                                 keepdim=True) * sigma_color)
        w9 = torch.exp(torch.sum(torch.pow(self.input[:, :, 2:, :] - self.input[:, :, :-2, :], 2), dim=1,
                                 keepdim=True) * sigma_color)
        w10 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-2, :] - self.input[:, :, 2:, :], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w11 = torch.exp(torch.sum(torch.pow(self.input[:, :, :, 2:] - self.input[:, :, :, :-2], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w12 = torch.exp(torch.sum(torch.pow(self.input[:, :, :, :-2] - self.input[:, :, :, 2:], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w13 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-2, :-1] - self.input[:, :, 2:, 1:], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w14 = torch.exp(torch.sum(torch.pow(self.input[:, :, 2:, 1:] - self.input[:, :, :-2, :-1], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w15 = torch.exp(torch.sum(torch.pow(self.input[:, :, 2:, :-1] - self.input[:, :, :-2, 1:], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w16 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-2, 1:] - self.input[:, :, 2:, :-1], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w17 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-1, :-2] - self.input[:, :, 1:, 2:], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w18 = torch.exp(torch.sum(torch.pow(self.input[:, :, 1:, 2:] - self.input[:, :, :-1, :-2], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w19 = torch.exp(torch.sum(torch.pow(self.input[:, :, 1:, :-2] - self.input[:, :, :-1, 2:], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w20 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-1, 2:] - self.input[:, :, 1:, :-2], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w21 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-2, :-2] - self.input[:, :, 2:, 2:], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w22 = torch.exp(torch.sum(torch.pow(self.input[:, :, 2:, 2:] - self.input[:, :, :-2, :-2], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w23 = torch.exp(torch.sum(torch.pow(self.input[:, :, 2:, :-2] - self.input[:, :, :-2, 2:], 2), dim=1,
                                  keepdim=True) * sigma_color)
        w24 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-2, 2:] - self.input[:, :, 2:, :-2], 2), dim=1,
                                  keepdim=True) * sigma_color)
        p = 1.0
 
        pixel_grad1 = w1 * torch.norm((self.output[:, :, 1:, :] - self.output[:, :, :-1, :]), p, dim=1, keepdim=True)
        pixel_grad2 = w2 * torch.norm((self.output[:, :, :-1, :] - self.output[:, :, 1:, :]), p, dim=1, keepdim=True)
        pixel_grad3 = w3 * torch.norm((self.output[:, :, :, 1:] - self.output[:, :, :, :-1]), p, dim=1, keepdim=True)
        pixel_grad4 = w4 * torch.norm((self.output[:, :, :, :-1] - self.output[:, :, :, 1:]), p, dim=1, keepdim=True)
        pixel_grad5 = w5 * torch.norm((self.output[:, :, :-1, :-1] - self.output[:, :, 1:, 1:]), p, dim=1, keepdim=True)
        pixel_grad6 = w6 * torch.norm((self.output[:, :, 1:, 1:] - self.output[:, :, :-1, :-1]), p, dim=1, keepdim=True)
        pixel_grad7 = w7 * torch.norm((self.output[:, :, 1:, :-1] - self.output[:, :, :-1, 1:]), p, dim=1, keepdim=True)
        pixel_grad8 = w8 * torch.norm((self.output[:, :, :-1, 1:] - self.output[:, :, 1:, :-1]), p, dim=1, keepdim=True)
        pixel_grad9 = w9 * torch.norm((self.output[:, :, 2:, :] - self.output[:, :, :-2, :]), p, dim=1, keepdim=True)
        pixel_grad10 = w10 * torch.norm((self.output[:, :, :-2, :] - self.output[:, :, 2:, :]), p, dim=1, keepdim=True)
        pixel_grad11 = w11 * torch.norm((self.output[:, :, :, 2:] - self.output[:, :, :, :-2]), p, dim=1, keepdim=True)
        pixel_grad12 = w12 * torch.norm((self.output[:, :, :, :-2] - self.output[:, :, :, 2:]), p, dim=1, keepdim=True)
        pixel_grad13 = w13 * torch.norm((self.output[:, :, :-2, :-1] - self.output[:, :, 2:, 1:]), p, dim=1, keepdim=True)
        pixel_grad14 = w14 * torch.norm((self.output[:, :, 2:, 1:] - self.output[:, :, :-2, :-1]), p, dim=1, keepdim=True)
        pixel_grad15 = w15 * torch.norm((self.output[:, :, 2:, :-1] - self.output[:, :, :-2, 1:]), p, dim=1, keepdim=True)
        pixel_grad16 = w16 * torch.norm((self.output[:, :, :-2, 1:] - self.output[:, :, 2:, :-1]), p, dim=1, keepdim=True)
        pixel_grad17 = w17 * torch.norm((self.output[:, :, :-1, :-2] - self.output[:, :, 1:, 2:]), p, dim=1, keepdim=True)
        pixel_grad18 = w18 * torch.norm((self.output[:, :, 1:, 2:] - self.output[:, :, :-1, :-2]), p, dim=1, keepdim=True)
        pixel_grad19 = w19 * torch.norm((self.output[:, :, 1:, :-2] - self.output[:, :, :-1, 2:]), p, dim=1, keepdim=True)
        pixel_grad20 = w20 * torch.norm((self.output[:, :, :-1, 2:] - self.output[:, :, 1:, :-2]), p, dim=1, keepdim=True)
        pixel_grad21 = w21 * torch.norm((self.output[:, :, :-2, :-2] - self.output[:, :, 2:, 2:]), p, dim=1, keepdim=True)
        pixel_grad22 = w22 * torch.norm((self.output[:, :, 2:, 2:] - self.output[:, :, :-2, :-2]), p, dim=1, keepdim=True)
        pixel_grad23 = w23 * torch.norm((self.output[:, :, 2:, :-2] - self.output[:, :, :-2, 2:]), p, dim=1, keepdim=True)
        pixel_grad24 = w24 * torch.norm((self.output[:, :, :-2, 2:] - self.output[:, :, 2:, :-2]), p, dim=1, keepdim=True)
 
        ReguTerm1 = torch.mean(pixel_grad1) \
                    + torch.mean(pixel_grad2) \
                    + torch.mean(pixel_grad3) \
                    + torch.mean(pixel_grad4) \
                    + torch.mean(pixel_grad5) \
                    + torch.mean(pixel_grad6) \
                    + torch.mean(pixel_grad7) \
                    + torch.mean(pixel_grad8) \
                    + torch.mean(pixel_grad9) \
                    + torch.mean(pixel_grad10) \
                    + torch.mean(pixel_grad11) \
                    + torch.mean(pixel_grad12) \
                    + torch.mean(pixel_grad13) \
                    + torch.mean(pixel_grad14) \
                    + torch.mean(pixel_grad15) \
                    + torch.mean(pixel_grad16) \
                    + torch.mean(pixel_grad17) \
                    + torch.mean(pixel_grad18) \
                    + torch.mean(pixel_grad19) \
                    + torch.mean(pixel_grad20) \
                    + torch.mean(pixel_grad21) \
                    + torch.mean(pixel_grad22) \
                    + torch.mean(pixel_grad23) \
                    + torch.mean(pixel_grad24)
        total_term = ReguTerm1
        return total_term

有点长，但是基本都在重发一个事，那就是算相邻点的梯度，它先将输入图像从 RGB 色彩空间转换为 YCbCr 色彩空间，接着计算输出图像在不同方向（水平、垂直、对角线等）上的像素梯度，并利用输入图像的颜色差异生成权重，将这些加权后的梯度进行求和，得到正则化项，以此作为损失值，用于引导模型输出更平滑的图像。也就是说图像变化大的区域给予更小的权重从而调节尺度越大，变化小就很平滑了权重小就不怎么去调整。