【DDPM】

背景

单层VAE的原理和公式

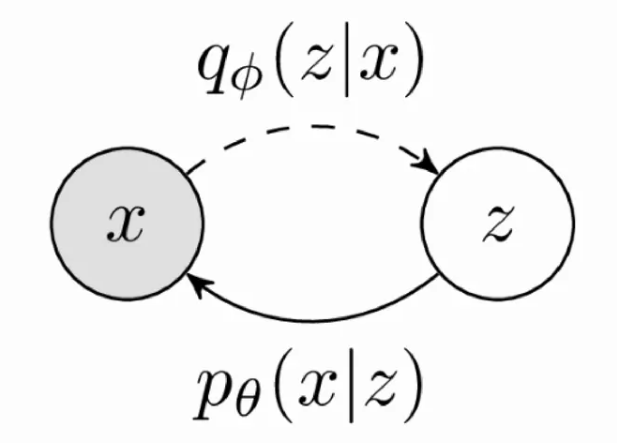
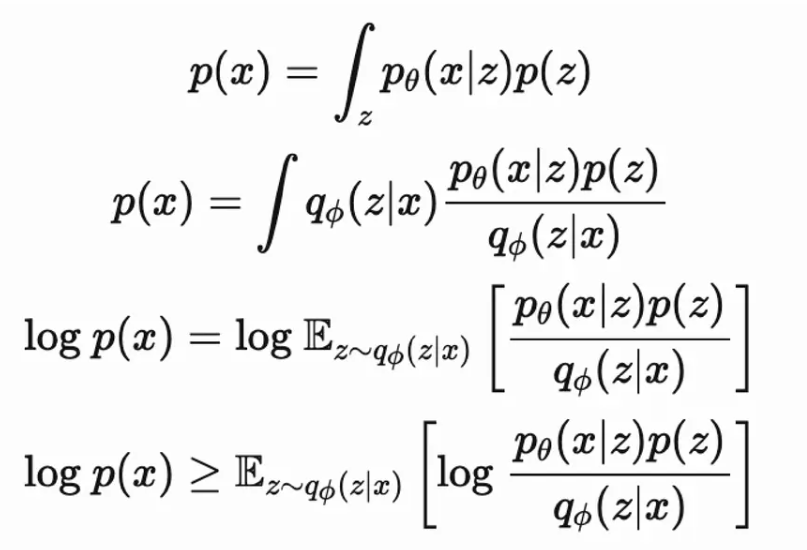
对于给定的公式，我们要理解如何应用Jensen’s不等式来从积分形式得到期望形式，特别是在变分自编码器（VAE）和变分推断中。这里的关键步骤是应用Jensen’s不等式来处理对数和期望。
第一个公式定义了边缘概率 $p(x)$：
$$p(x)={\int }_z{q}_{\varphi }(z|x)\frac{p_{\theta }(x|z)p(z)}{q_{\varphi }(z|x)}dz$$
可以看到，这个表达式是隐变量 $z$的积分，其中 $q_{\varphi }(z|x)$是对真实后验分布 $p_{\theta }(z|x)$的一个近似。
现在，我们想要计算 $p(x)$的对数 $\log p(x)$：
$$\log p(x)=\log {\int }_z{q}_{\varphi }(z|x)\frac{p_{\theta }(x|z)p(z)}{q_{\varphi }(z|x)}dz$$
直接对这个积分取对数是不可行的，因为对数运算不能简单地穿透积分符号。为了解决这个问题，我们使用Jensen’s不等式，该不等式允许我们将对数函数的期望与期望的对数进行比较。由于对数是一个凹函数（即它的二阶导数为负），我们可以将不等式应用于期望的内部：
$$\log p(x)\ge {\mathbb{E}}_{z\sim q_{\varphi }(z|x)}\left[\log \frac{p_{\theta }(x|z)p(z)}{q_{\varphi }(z|x)}\right]$$
这里，我们把 $\frac{p_{\theta }(x|z)p(z)}{q_{\varphi }(z|x)}$视为一个关于 $z$的函数，然后计算这个函数在变分分布 $q_{\varphi }(z|x)$下的期望。根据Jensen’s不等式，我们知道对于凹函数（如对数函数），期望的对数小于等于对数的期望：

$\log \mathbb{E}[X]\le \mathbb{E}[\log X]$

但在我们的情况中，$X$是 $\frac{p_{\theta }(x|z)p(z)}{q_{\varphi }(z|x)}$，并且我们对这个比率的对数取期望，这是因为对数是凹的，我们得到了一个不等式，它给出了 $\log p(x)$的一个下界。

这个下界，也就是ELBO，可以用来近似最大化 $\log p(x)$，它是变分自编码器优化目标的核心。在实践中，我们调整 $q_{\varphi }(z|x)$来最大化这个下界，这样可以使 $q_{\varphi }(z|x)$尽可能地接近真实的后验分布 $p_{\theta }(z|x)$，并提升模型的整体性能。

一. 正向传播

(一)正向传播过程

给定初始数据分布$x_0\sim q\left(x\right)$，可以不断地向分布中添加高斯噪声，该噪声的标准差是以固定值${\beta }_t$而且是确定的，均值是以固定值${\beta }_t$和当前t时刻的数据$x_t$决定的。正向过程是一个固定的马尔可夫链，它按照一个方差调度表${\beta }_1,...,{\beta }_T$ 逐步地向数据添加高斯噪声。
$$p_{\theta }\left({\mathbf{x}}_{0:T}\right)=p\left({\mathbf{x}}_T\right)\prod _{t=1}^T{p}_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)$$

• 其中，$q(x_{1:T}|x_0)$：这是在给定初始数据点 $x_0$的条件下，随着时间推进，数据点经历的扩散过程的概率分布。它定义为一系列条件分布的乘积${\prod }_{t=1}^{T}q(x_t|x_{t-1})$，这表示每一步$t$的数据 $x_t$只依赖于前一步$t-1$的数据 $x_{t-1}$。
  $$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right)=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I}\right)$$
• 每一步的条件分布 $q(x_t|x_{t-1})$ 是高斯分布$\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$ ，其中$\mathcal{N}$ 表示正态分布，$\sqrt{1-{\beta }_t}{x}_{t-1}$是均值，表示 $x_t$ ) 在$x_{t-1}$的基础上加入了缩放的噪声，而 ${\beta }_{t}I$ 是协方差矩阵，表示添加的噪声的大小。

简单来说，这个过程模拟了如何将一个干净的数据点 $x_0$逐步转化为更加随机的形式 $x_T$。通过多个步骤逐渐增加噪声，每一步都按照一个预设的方差调度表来确定噪声的量。这个正向过程为生成模型提供了一种方式来逆向生成干净的数据点，从而可以使用模型来生成新的数据点。最后随着t的不断增大，最终的数据分布$x_T$变成了一个各向独立的高斯分布，也就是说无限接近于高斯白噪声。

(二)任意时刻$q\left(x_t\right)$的表达 （*）

现在我们想象一下抛骰子，我需要两个骰子的点数之和，每次投掷骰子的概率近似为一个正态分布。那么，一次投掷两个骰子的概率分布应该等同于每次独立投掷一个骰子的概率叠加（类似于卷积）
$$N\left({\mu }_1,{{\sigma }_1}^2\right)+N\left({\mu }_2,{{\sigma }_2}^2\right)=N\left({\mu }_1+{\mu }_2,{{\sigma }_1}^2+{{\sigma }_2^2}^2\right)$$
有了这个公式之后，我们先计算两次传播过程

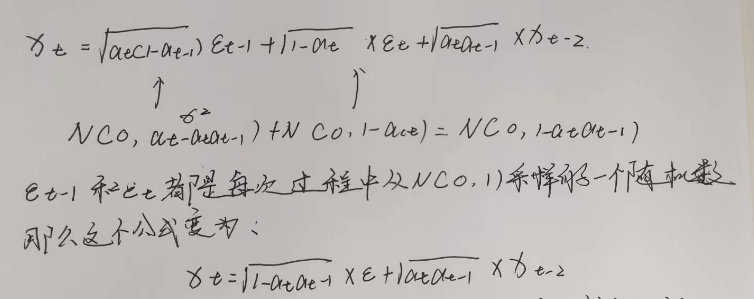
最后，我们可以直接从原始数据点$x_0$出发，通过应用一系列的缩放因$\sqrt{{\bar{\alpha }}_t}$和噪声级别$1-{\bar{\alpha }}_t$来得到任意时间步$t$的数据点$x_t$的分布。这是因为正向过程中每一步的噪声加入是累积的，可以通过${\bar{\alpha }}_t$这个累积噪声水平来直接计算。这种性质使得扩散模型在理论上和实践上都很有吸引力，因为它允许跳过时间步骤之间的顺序依赖，直接进行采样。我们就可以由$x_0$和当前时刻的噪声直接推断出$x_t$。

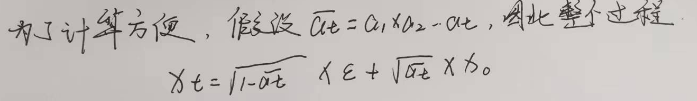
二. 逆扩散过程（Reverse Process）

这个过程包括了从一个简单的分布开始，逐步逆向去噪声，恢复出原始的数据点。从高斯分布中回复原始数据，也就是从$x_T$恢复出$x_0$。但是无法逐步的去拟合分布，所以需要构建一个参数分布去估计。整个过程仍然是一个马尔可夫链。
$$q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right):=\prod _{t=1}^{T}q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right)$$
$$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right):=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I}\right)$$
其中，

• $p_{\theta }(x_0)$：这是模型对原始数据点$x_0$ 的概率估计。

• $\int p_{\theta }(x_{0:T})d{x}_{1:T}$：这是一个积分，表示对所有潜变量$x_1$ 到$x_T$ 的积分，这些潜变量构成了从$x_0$ 到$x_T$ 的过渡路径。

• $x_0\sim q(x_0)$：表示数据点$x_0$ 是从实际数据分布$q(x_0)$ 中采样的。

• $p_{\theta }(x_{0:T})$：这是$x_0$ 到$x_T$ 的联合分布，它通过潜变量序列$x_1$ 到$x_T$ 定义。

• $p_{\theta }(x_T)=\mathcal{N}(x_T;0,I)$：这是初始条件，表示最终的潜变量$x_T$ 是从标准正态分布中采样的。

• $p_{\theta }(x_{0:T})$ 的定义：公式中的乘积${\prod }_{t=1}^T{p}_{\theta }(x_{t-1}|x_t)$ 表示从$x_T$ 开始，通过一系列条件分布$p_{\theta }(x_{t-1}|x_t)$ 逆向生成$x_0$ 的过程。

• 每个条件分布$p_{\theta }(x_{t-1}|x_t)$ 定义为一个高斯分布$\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\Sigma }_{\theta }(x_t,t))$，其中${\mu }_{\theta }(x_t,t)$ 和${\Sigma }_{\theta }(x_t,t)$ 是由模型学习的，它们定义了如何从$x_t$ 转换到$x_{t-1}$。

总的来说，这段文本和公式详细描述了如何通过一个由数据生成过程反向构建的马尔可夫链来估计原始数据点的概率。这个过程包括了从一个简单的分布开始，逐步逆向去噪声，恢复出原始的数据点。这种方法在生成模型中特别有用，例如在图像和音频生成任务中。

三. 求解后验扩散条件概率过程（Reverse Process）（*）

三. 目标数据分布的似然函数

如何训练 Diffusion Models 以求得公式 (3) 中的均值 μθ(xt，t) 和方差 Σθ (xt，t) 呢？ 在 VAE 中我们学过极大似然估计的作用：对于真实的训练样本数据已知，要求模型的参数，可以使用极大似然估计。

如何训练 Diffusion Models 以求得公式 (3) 中的均值 μθ(xt，t) 和方差 Σθ (xt，t) 呢？ 在 VAE 中我们学过极大似然估计的作用：对于真实的训练样本数据已知，要求模型的参数，可以使用极大似然估计。(参考)

我们可以在负对数似然函数的基础上加上一个KL散度，于是就构成了负对数似然的上界了，上界越小，负对数似然自然也就越小那么对数似然就越大了：

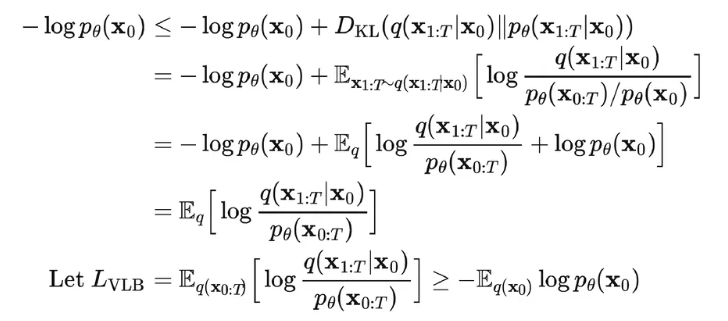
进一步可以写出交叉熵的上界，接下来，我们可以对交叉熵的上界进行化简

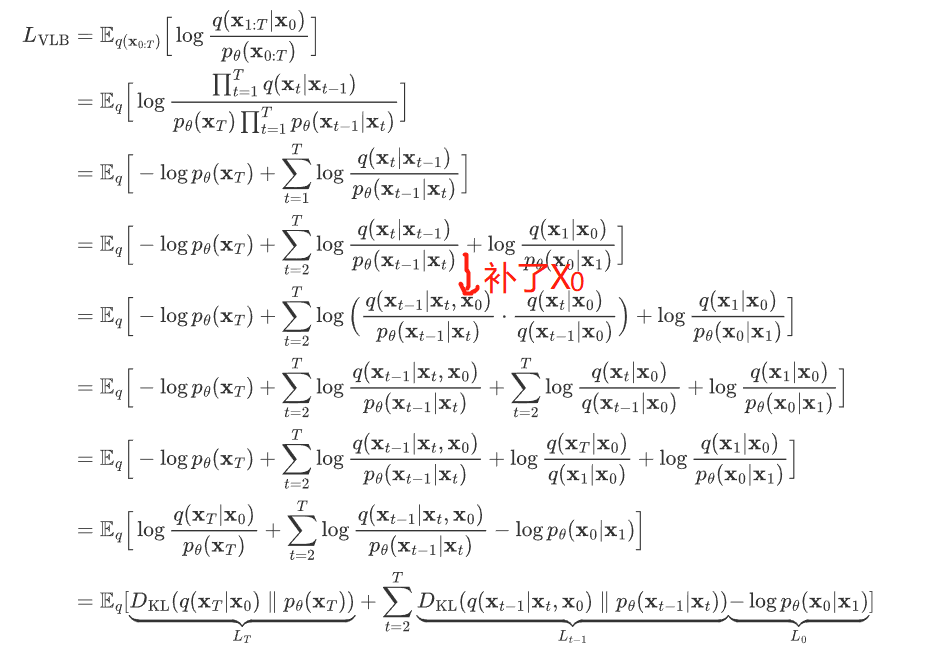
四. 总结

1. Diffusion Model 通过参数化的方式表示为马尔科夫链，这意味着隐变量 x1,…xT 都满足当前时间步 t 只依赖于上一个时间步 t-1，这样对后续计算很有帮助。
2. 马尔科夫链中的转变概率分布 pθ(xt-1|xt) 服从高斯分布，在正向扩散过程当中高斯分布的参数是直接设定的，而逆向过程中的高斯分布参数是通过学习得到的。
3. Diffusion Model 网络模型扩展性和鲁棒性比较强，可以选择输入和输出维度相同的网络模型，例如类似于UNet的架构，保持网络模型的输入和输出 Tensor dims 相等。
4. Diffusion Model 的目的是对输入数据求极大似然函数，实际表现为通过训练来调整模型参数以最小化数据的负对数似然的变分上限
5. 在概率分布转换过程中，因为通过马尔科夫假设，目标函数第4点中的变分上限都可以转变为利用 KL 散度来计算，因此避免了采用蒙特卡洛采样的方式。