【Python】递推——（yacs）切蛋糕问题

【题目】一个圆型的蛋糕，切 nn 刀后，最多能将蛋糕分成多少块？当 n=3n=3 时，最多可以分成 77 块，如下图：

输入格式

• 单个整数：表示切割的次数 n。

输出格式

• 单个整数：表示最多能将蛋糕切成多少份。

数据范围

• 1≤n≤50001≤n≤5000。

---

【分析】我们可以列出不同刀数下，蛋糕最多可以被分为多少块

n=0时，蛋糕一整块，蛋糕最多1块

n=1时，蛋糕最多被切分为2块

n=2时，蛋糕最多被切分为4块

n=3时，蛋糕最多被切分为7块

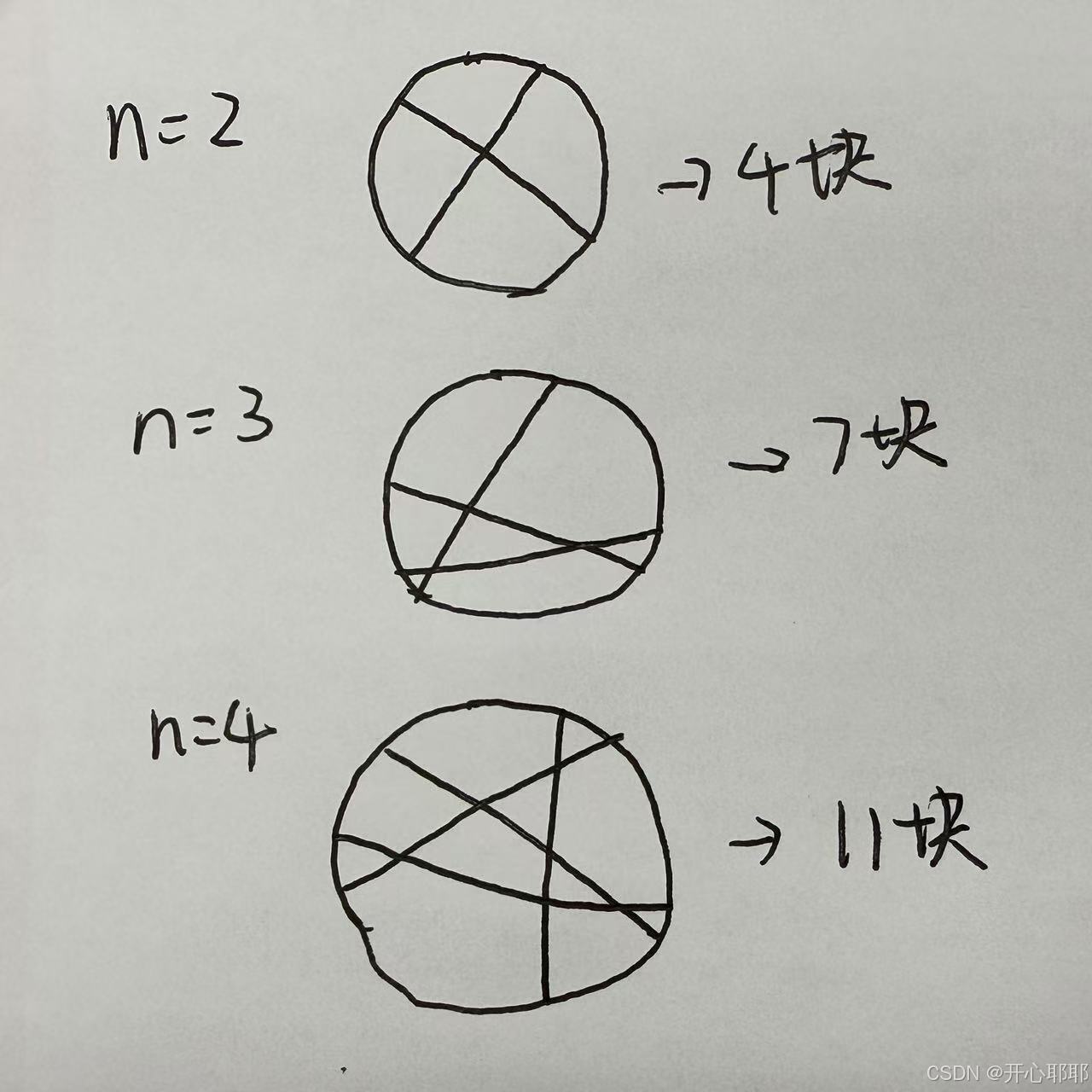
以此类推，切割的关键就在于新的每一刀都尽可能跟之前的所有刀痕相交

故我们可以得出刀数和蛋糕块数的关系，例如n=3时，是在n=2刀的基础上加上了3块，也就是在上一刀的基础上加上n

即可根据已知推出未知，也是【递推】的思想，递推的关键就是得出递推表达式和确定边界条件。

若定义一个函数，那表示第n刀切的块数，那么递推表达式即为：

n>=1时，

边界条件为n=0时，

---

为了模拟递推，我们可以利用Python中的列表，通过下标来存储每一刀对应的最大块数

# 读取输入
n = int(input())

# 初始化结果数组（其实不需要数组，只需要一个变量来存储结果）
# 但为了模拟过程，我们还是用一个列表来存储每一步的结果（可选）
a = [0] * (n + 1)  # 初始化一个长度为 n+1 的列表，因为 f(n) 需要用到 f(0) 到 f(n)

# 基础条件：没有切割时，蛋糕为一块
a[0] = 1

# 根据公式 f(n) = f(n-1) + n 计算切割后的块数
for i in range(1, n + 1):
    a[i] = a[i - 1] + i

# 输出结果，即切 n 刀后的最大块数
print(a[n])