pymc3学生成绩分析和预测（补充+翻译）_机器学习预测葡萄牙语学生成绩代码-CSDN博客

“age” 学生年龄从 15 到 22
“internet” 学生在家可以上网（二进制：是或否）
“failures” 是过去失败的次数（类别: n if 1<=n<3, else 4）
“higher” 想要接受高等教育（二进制：是或否）
“Medu” 母亲教育（类别：0-无，1-小学教育（四年级），2个五至九年级，3个中学教育或4个高等教育）
“”Fedu" 父亲的教育（类别：0-无，1-小学教育（四年级），2个五至九年级，3个中学教育或4个高等教育）
“studytime” 每周学习时间（类别：1 - <2 小时，2 - 2 到 5 小时，3 - 5 到 10 小时，或 4 - >10 小时）
“absences” 缺课次数（数值：从 0 到 93）

最后的数据集是这样的，这是葡萄牙语学生的成绩分布。

import seaborn as sns
sns.displot(data=df,x='G3',kde=True);

png

GLM:频率模型

首先，我将构建一个常规的 GLM statsmodels来说明频率论方法。

Internet 使用和Higher有两个二元分类特征。age是一个数字特征。其余的特征是数值，这些数值被划分为有序类别。从业者可能会根据模型目标和特征的性质对这些进行不同的处理。在这里，我将它们视为范围0到max(feature)内的数字。在 statsmodels 中，我们可以使用 patsy 设计矩阵和公式来指定我们希望如何处理每个变量。例如，对于分类，我们可以使用C(Internet, Treatment(0))将Internet编码为一个分类变量，参考水平设置为(0)。

import statsmodels.formula.api as smf

# model grade data
formula = [f"{f}" if f not in categoricals else f"C({f})" for f in features]
formula = f'{target[0]} ~ ' + ' + '.join(formula)
glm_ = smf.glm(formula=formula,
              data=df,
              family=sm.families.Gaussian())
glm = glm_.fit()
glm.summary()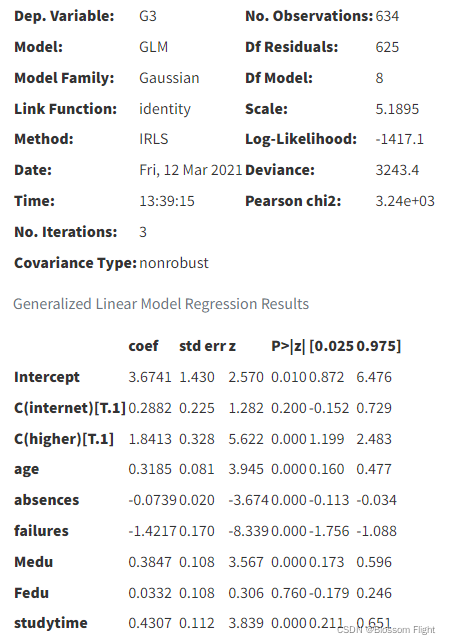

以上是一些快速的观察。除父亲教育程度外，大多数特征与成绩呈显著的线性关系。回归系数的符号也符合我们的逻辑。结果表明，更多的缺勤和不及格对预测成绩有负面影响。而学习时间和继续接受高等教育的愿望对预期成绩有积极的影响。

下面我们看到数据中有一个异常值。（最左侧）

png

PyMC3 GLM:贝叶斯模型

现在让我们使用 PyMC3 重新构建我们的模型。正如这篇博文中所述，PyMC3 有自己的glm.from_formula()功能，其行为类似于 statsmodels。它甚至接受相同的 patsy 公式。

NOTE 在pymc3中可以进行多种先验分布设定，如下：

Continuous — PyMC3 3.11.4 documentation

import pymc3 as pm
import arviz as avz

# note we can re-use our formula 
print(formula)

bglm = pm.Model()
with bglm:
    # Normally distributed priors
    family = pm.glm.families.Normal()
    # create the model 
    pm.GLM.from_formula(formula,data=df,family=family)
    # sample
    trace = pm.sample(1000,return_inferencedata=True)

以下为输出：
G3 ~ C(internet) + C(higher) + age + absences + failures + Medu + Fedu + studytime

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sd, studytime, Fedu, Medu, failures, absences, age, C(higher)[T.1], C(internet)[T.1], Intercept]

模型运行后，我们可以检查模型后验分布样本。这类似于如上所示查看常规 GLM 的model.summary()。在这个贝叶斯模型汇总表中，平均值是后验分布的系数估计值。这里我们看到模型截距的后验概率大约是4.9。不管我们对学生的了解如何，这表明学生至少应该得到4.9分。

summary = avz.summary(trace)
summary[:5]

NOTE:原文认为后验截距是4.9，但是表上是3.724，这里是不是有问题？对于arviz汇总表说明可以参考如下文档：

arviz.summary — ArviZ dev documentation

我们具有最高的后密度“HPD”而不是P值。3-97％的HPD字段和值范围表示我们参数真实值的可信间隔。如果这个范围超过0，从负面影响到正面影响，那么也许数据信号太弱，无法得出这个变量的结论。正如互联网使用的情况——可恶的新冠！

后验分布也可以看作是轨迹图。

avz.plot_trace(trace)

png

解释变量对预测成绩的影响

采样完成。我们可以探索每个特征如何影响和影响预测成绩。我在PyMC3 的Gist 中找到了函数model_affect()。

同样，缺勤次数对预期成绩有负面影响，年龄增长有积极的影响。

X = pd.DataFrame(data=glm_.data.exog,columns=glm_.data.param_names) # dmatrix
model_affect('absences',trace,X)
model_affect('age',trace,X)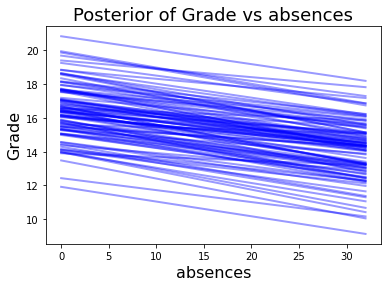

png

后验预测检查

进行后验预测检查 (PPC)以验证贝叶斯模型是否已捕获基础数据的真实分布。或者，PPC 用于评估真实数据分布与贝叶斯模型生成的数据分布的比较情况。根据 PyMC3 文档，PPC 也是贝叶斯建模工作流程的关键部分。PPC 有两个主要好处：

它们允许您检查您是否确实将科学知识融入了您的模型中——简而言之，它们可以帮助您在查看数据之前检查您的假设的可信度。
它们可以极大地帮助采样，特别是对于广义线性模型，其中结果空间和参数空间由于链接函数而发散。

下面，PPC 用于对我们模型的 Y 结果进行 200 次采样（左）。与上述跟踪图类似，PPC 还可以提供模型参数的采样，例如年龄（右）。

PNG

对样本外数据（测试集）的预测

既然模型已经过训练并适合数据，并且我们已经检查了变量影响，我们可以使用模型对样本外观察和测试用例进行预测。与其他建模方法和包（例如 statsmodels 和 scikit-learn）相比，它不像简单地调用model.predict(Xdata). 在 PyMC3 中，我发现了几种将模型应用于样本外数据的策略。

方法一：平均系数模型

我们可以使用 MCMC 轨迹来获得每个模型系数的样本平均值，并将其应用于重建典型的 GLM 公式。记住我们用statsmodels-patsy公式来编码我们的分类变量，我们也可以用patsy来构造一个助手。

这种方法的好处是它的易用性和简单性。不利的一面是，我们现在忽略并错过了 MCMC 抽样的一部分，因为我们首先采用贝叶斯方法获得了数据的置信度和不确定性。

# mean model coefficients
mean_model = summary[['mean']].T.reset_index(drop=True)

# create a  design matrix of exog data values
# same as for GLM's
X = pd.DataFrame(data=glm_.data.exog,columns=glm_.data.param_names)

# add columns for the standard deviations output from the bayesian fit
for x in mean_model.columns:
    if x not in X.columns:
        X[x] = 1
        
# multiply and work out mu predictions
coefs = X * mean_model.values
pred_mu = coefs.iloc[:,:-1].sum(axis=1)[:]
pred_sd = coefs['sd']
print('Predictions:')
n = 5
for m,s in zip(pred_mu[:n],pred_sd[:n]): print(f"\tMu:{m:.2f} Sd:{s:.2f}")

Predictions:
	Mu:13.47 Sd:2.29
	Mu:12.34 Sd:2.29
	Mu:11.41 Sd:2.29
	Mu:13.48 Sd:2.29
	Mu:12.72 Sd:2.29

注意：使用 Jupyter、pymc3.GLM 和 Theano 时存在问题。在撰写本文时，这就是pm.GLM.from_formula()使用 Jupyter 开始崩溃的地方。PyMC3 文档中推荐了以下两种方法。但是，当与GLM.from_formula()Jupyter结合使用时，两者都会产生以下 Theano 错误。ERROR! Session/line number was not unique in database. History logging moved to new session 11这似乎是 GLM.from_formula() 在 Jupyter Notebooks 中使用 patsy 并与 Theano 交互的方式的问题。

source code
question on SO
我尚未测试使用 .py 脚本运行以下任一方法，但以下方法在 Jupyter 之外工作似乎是合理的。

方法二：使用Theano共享变量

鉴于上述情况，现在我们将丢失GLM.from_formula()和重建标准 PyMC3 形式的模型，并使用两者：patsy 生成设计矩阵，和 Theano 创建共享 X 变量。为了简短起见，我使用shape(n). 这将降低模型调整性能，因为所有先验都设置为统一的初始值，并且可能导致一些零错误，例如参见此处。在实践中，您应该使用信息先验单独设置 Beta。

import patsy
from theano import shared

design = patsy.dmatrices(formula_like=formula,data=df,return_type='dataframe')
# design[1].design_info

train,test = df[:500],df[500:]
trainx = patsy.build_design_matrices([design[1].design_info],train,return_type="dataframe")[0]
testx = patsy.build_design_matrices([design[1].design_info],test,return_type="dataframe")[0]

# Shared theano variable for modeling
# must be np.array()
modelx = shared(np.array(trainx))

bglm = pm.Model()
with bglm:
    alpha = pm.Normal('alpha', mu=4, sd=10)
    betas = pm.Normal('beta', mu=1, sd=6, shape=8)
    sigma = pm.HalfNormal('sigma', sd=1)a)
    mu = alpha + pm.math.dot(betas, modelx.T)
    likelihood = pm.Normal('y', mu=mu, sd=sigma, observed=trainy)  
    trace = pm.sample(1000,init="adapt_diag",return_inferencedata=True)

现在我们可以用测试集更新我们共享的 X 变量并使用模型进行预测。这里的预测实际上意味着对测试集观测值的每个系数的后验分布进行采样。

我们可以指定采样轮数来执行和可视化单个样本和样本聚合。

samples = 50

# Update model X and make Prediction
modelx.set_value(np.array(testx)) # update X data
ppc = pm.sample_posterior_predictive(trace, model=bglm, samples=samples,random_seed=6)
print(ppc['y'].shape)

n = 5
plt.figure(figsize=(15,3))
plt.title('Observed & Predicted Grades')
plt.plot(test.reset_index()['G3'],'k-',label='Y observed')
plt.plot(ppc['y'][0,:],lw=1,linestyle=':',c='grey',label='Y 1st trace')
plt.plot(ppc['y'][:n,:].mean(axis=0),lw=1,linestyle='--',c='grey',label=f'Y trace [0:{n}]th mean')
plt.legend(bbox_to_anchor=(1,1));

PNG

方法三：共享X变量

这种方法与上面的非常相似，但pm.Data()在训练和测试轮次中使用来保存我们的 X 数据。从功能上讲，这更干净，因为我们不需要shared()明确导入和使用 Theano 。

bglm = pm.Model()
with bglm:
    alpha = pm.Normal('alpha', mu=4, sd=10)
    betas = pm.Normal('beta', mu=1, sd=6, shape=8)
    sigma = pm.HalfNormal('sigma', sd=1)
    xdata = pm.Data("pred", trainx.T)
    mu = alpha + pm.math.dot(betas, xdata)
    likelihood = pm.Normal('y', mu=mu, sd=sigma, observed=trainy)
    trace = pm.sample(1000,init="adapt_diag",return_inferencedata=True)

# Update X values and predict outcomes and probabilities
with bglm:
    pm.set_data({"pred": testx.T})
    posterior_predictive = pm.sample_posterior_predictive(trace, var_names=["y"], samples=600)
    model_preds = posterior_predictive["y"]

再次，让我们增加样本数量，将以下内容可视化：

OOS 测试数据中每次观测值的后验分布（左）
以及使用 arviz 的 Observed、Mean、Credible-Interval 或“Highest Density Interval” hdi()。

from matplotlib.gridspec import GridSpec

fig=plt.figure(figsize=(15,5))
gs=GridSpec(nrows=1,ncols=2,width_ratios=[1,2]) # 2 rows, 3 columns

ax0 = fig.add_subplot(gs[0])
ax0.set_title("Yi kde")
sns.kdeplot(data=pd.DataFrame(model_preds[:,:5]),ax=ax0)

ax1 = fig.add_subplot(gs[1])
ax1.set_title("test predictions")
ax1.plot(test.reset_index(drop=True)['G3'],'k-',lw=1,label='obs')
ax1.plot(model_preds.mean(0),c='orange',label='mean pred')

alpha = 1-0.5
ax1.plot(avz.hdi(model_preds,alpha)[:,0],ls='--',lw=1,c='red',label=f'CI lower {alpha}')
ax1.plot(avz.hdi(model_preds,alpha)[:,1],ls='--',lw=1,c='red',label=f'CI upper {alpha}')

ax1.legend(bbox_to_anchor=(1,1));

png