目录
提要
计算几何精度很重要,eps处理精度要到位!不要畏惧代码的长度,难度并不高,重点还是精度
叉乘 a×b=absinα α为由a逆时针转向b的夹角
可能的坑:多边形不能是一条线! 如果题目可能有这种坑,请提前判断多边形的所有点是否共线
参考文献
特别鸣谢张姐和袁姐的精彩讲解
总模板
#include<cstdio> //计算几何基础 代码 https://blog.csdn.net/qq_44691917/article/details/104686146
#include<iostream>//理论https://www.luogu.com.cn/blog/wjyyy/geometry1
#include<cmath>//自己写的总结 https://mp.csdn.net/mp_blog/creation/editor/120031148
#include<vector>//可能的坑:多边形不能是一条线! 如果题目可能有这种坑,请提前判断多边形的所有点是否共线
#include<algorithm>
using namespace std;
#define Vector Point//向量在数学意义上是矢量,但是计算机并不能存储方向,因此还是要用坐标表示,但是因为一些函数是基于向量计算的,与点没有关系,为了区别开我们重定义向量名Vector
#define Segment Line//可以用两个点表示线段,起点是p1,终点是p2。直接用直线的数据结构定义线段
//typedef vector<Point> Polygon;//用点集描绘多边形 在134行定义,现在头文件标注一下
const double PI=acos(-1.0);
const double eps=1e-8;
/* 目录 10~88行为点和向量专题 90-144行后为点和线专题 146-173为多边专题 175后为凸包-旋转卡壳专题*/
inline int sgn(double d) { //判断浮点数符号 正数返回1 0返回0 负数返回-1
if(fabs(d)<eps) return 0;
return d>0?1:-1;
}
inline int cmp(double x,double y) { //浮点数比较大小 x>y返回1,x=y返回0,x<y返回-1
return sgn(x-y);
}
struct Point {//点Point 向量Vector共用同一个数据结构
double x,y;
Point(double a=0.0,double b=0.0):x(a),y(b) {}//结构体初始化 https://blog.csdn.net/qq_54886579/article/details/120024152
Vector operator + (Vector B) {//重载运算符
return Vector(x+B.x,y+B.y);
}
Vector operator - (Point B) {//两个点作差将得到一个向量。向量之间的减法“共起点,指被减”,这里的起点在二维坐标系中指原点。向量A-B得到BA
return Vector(x-B.x,y-B.y);
}
Vector operator * (double d) { //数乘 注意double要放在*后面 不然报错
return Vector(x*d,y*d);
}
double operator * (Vector B) { //数量积
return x*B.x+y*B.y;
}
Vector operator / (double d) {//向量与实数相除得到等比例缩放的向量
return Vector(x/d,y/d);
}
double operator ^ (Vector B) { //叉乘 用^表示 等价于空间坐标系z轴为0的叉乘
return x*B.y-y*B.x;
}
bool operator < (const Point &b) const {//用于对点集排序 先比x再比y
if(sgn(x-b.x)==0) return y<b.y;
return x<b.x;
}
bool operator == (const Point& b) const {
if(sgn(x-b.x)==0 && sgn(y-b.y)==0)
return true;
return false;
}
};
double norm(Vector A) { //模长
return sqrt(A*A);
}
double sqrnorm(Vector A) { //模长平方
return A*A;
}
double angle(Vector A,Vector B) { //向量夹角
return acos(A*B/norm(A)/norm(B));
}
Vector rotate(Vector A,double rad) { //逆时针旋转 x'=xcosα-ysinα y'=xsinα+ycosα
return Vector(A.x*cos(rad)-A.y*sin(rad), A.x*sin(rad)+A.y*cos(rad));
}
Vector normal(Vector A) { //计算向量逆时针旋转九十度(即单位法向量) x'=-y y'=x 然后再除以模长即可
double L=norm(A);
return Vector(-A.y/L, A.x/L);
}
bool ToLeftTest(Point c, Point a, Point b) { //逆时针方向的边 a为起点 b为终点 c为边外一点 判断c是否在ab的左边 ab^ac
return ((b-a)^(c-a))>0;
}
double Distance(Point a,Point b) { //两点之间的距离 点a到点b的距离
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
struct Line { //直线的表示:线上两个点 Segment线段和直线Line通过typedef共用同一个数据结构
Point p1,p2;
Line(Point a,Point b):p1(a),p2(b) {}
};
//点和直线的位置关系 点在直线左边返回1 右边返回2 在直线上返回0
int PointLineRelation(Point p,Line v) { //在二维平面上有3种,即点在直线左侧,在右侧,在直线上。用直线上两点p1,p2与点p构成两个向量,用叉积的正负判断方向,就能得到位置关系。
int c=sgn((p-v.p1)^(v.p2-v.p1));//向量p1p 叉乘 p1p2
if(c<0) return 1;
if(c>0) return 2;
return 0;
}
//点和线段的位置关系 0为不在线段上,1为在线段上
bool PointOnSeg(Point p,Segment v) { //判断点p是否在线段v上,先用叉积判断是否共线,然后用点积看p和v的两个端点产生的角是否为钝角。
return sgn((p-v.p1)^(v.p2-v.p1)) ==0 && sgn((p-v.p1)*(p-v.p2))<=0;
}
//点到直线的距离 已知点p和直线v(p1,p2),求p到v的距离。首先用叉积求p、p1、p2构成的平行四边形的面积 然后用面积除以平行四边形的底边长,也就是线段(p1,p2)的长度,就得到了平行四边形的高,即p点到直线的距离。
double DisPointLine(Point p,Line v) {
return fabs((p-v.p1)^(v.p2-v.p1))/Distance(v.p1,v.p2);
}
int LineRelation(Line v1,Line v2) { //两条直线的位置关系 用两条直线方向向量叉乘来判断 等于0则判断平行还是重合 否则相交 0 平行 1 重合 2 相交
if(sgn((v1.p2-v1.p1)^(v2.p2-v2.p1))==0) {
if(PointLineRelation(v1.p1,v2)==0) return 1;//1 重合
else return 0;//0 平行
} else return 2; //2 相交
}
bool CrossSegment(Line l1,Line l2) { //判断两直线是否相交
Point a=l1.p1,b=l1.p2,c=l2.p1,d=l2.p2;//如果一条线段的两端在另一条线段的两侧,那么两个端点与另一线段产生的两个叉积正负相反
double c1=(b-a)^(c-a),c2=(b-a)^(d-a);//也就是说两个叉积相乘为负。如果两条线段互相满足这一点,那么就是相交的
double d1=(d-c)^(a-c),d2=(d-c)^(b-c);//c1=AB^AC c2=AB^AD d1=CD^CA d2=CD^CB
return sgn(c1)*sgn(c2)<0 && sgn(d1)*sgn(d2)<0;
}
Point CrossPoint(Line l1,Line l2) { //两直线交点(叉乘公式) 解释见代码下方注释区 注意两直线不能重合,否则会输出nan,可以用isnan来进行判断和维护鲁棒性
Point a=l1.p1,b=l1.p2,c=l2.p1,d=l2.p2;
double s1=(d-a)^(c-a),s2=(c-b)^(d-b),s=s1/(s1+s2);
Point t=b-a;
return a+t*s;
}
Point project(Point p, Segment s) {//求点p在直线s上的投影
Vector base = s.p2 - s.p1;
double r = ( (p - s.p1)* base) / sqrnorm(base);
base = base * r;
return Point(s.p1 + base);
}
inline double DisPointSeg(Point C,Point A, Point B) {//点到线段的距离 计算C点到线段AB的最短距离
if (Distance(A, B) < eps) return Distance(B, C);//AB是同一点
if ((B-A)*(C-A)<-eps) return Distance(A,C);//AB*AC<0 点的投影落在线段之外且与A同侧 支点A离C最近
if ((A-B)*(C-B)<-eps) return Distance(B,C);//BA*BC<0 点的投影落在线段之外且与B同侧 支点B离C最近
Line l=Line(A,B);//点的投影落在线段内,直接计算点线距
return DisPointLine(C,l);
}
inline double DislineLine(Point A, Point B, Point C, Point D) {//求线段AB与CD之间的距离(一条线段的两端点到另外一条线段的最小距离),反过来一样,共4种情况
return min( min(DisPointSeg(C,A,B),DisPointSeg(D,A,B)) , min(DisPointSeg(A,C,D),DisPointSeg(B,C,D)) );
}
typedef vector<Point> Polygon;
int PointInPolygon(Point pt,Polygon p) { //判断点Pt与多边形的位置关系 0外部 1内部 2边上 3顶点上
int n=p.size();
for(int i=0; i<n; i++) if(p[i]==pt) return 3; //点在顶点上
for(int i=0; i<n; i++) {
Line v=Line(p[i],p[(i+1)%n]);
if(PointOnSeg(pt,v)) return 2;//点在边上
}
int cnt=0;
for(int i=0; i<n; i++) {
int j=(i+1)%n;//i为起点 j为终点
bool c=ToLeftTest(pt,p[i],p[j]);
int u=sgn(p[i].y-pt.y),v=sgn(p[j].y-pt.y);
if(c && u<0 && v>=0) cnt++;
if(!c && u>=0 && v<0) cnt--;
}
return cnt!=0;//1 内部 0 外部
}
double Polygon_Area(Polygon p) { //求多边形面积,n为多边形顶点数
double area=0;
int n=p.size();
for(int i=0; i<n; i++) area+=(p[i]^p[(i+1)%n]);
return fabs(area/2);
}
Polygon Andrew(Polygon p) {//返回凸包 时间复杂度O(nlogn) 多边形不能是一条线!
int n=p.size();
sort(p.begin(),p.end());
Polygon ch;//凸包结果
for(int i=0; i<n; i++) { //起点不能出队 所以size>1
while(ch.size()>1 && !ToLeftTest(p[i],ch[ch.size()-2],ch[ch.size()-1])) { //下凸包 如果上一条边到这一条边不符合左旋要求,上一个点出队
// printf("update: segment %d TO %d destination: %d\n",ch.size()-2,ch.size()-1,i);
ch.pop_back();
}
ch.push_back(p[i]);//这一个点入队
// printf("ch[ %d ]= %d\n",ch.size()-1,i);
}
int k=ch.size();
for(int i=n-2; i>=0; i--) { //从p的倒数第二个点开始,因为下凸包终点是倒数第一个点,倒数第一个点就是上凸包的起点
while(ch.size()>k && !ToLeftTest(p[i],ch[ch.size()-2],ch[ch.size()-1])) { //上凸包 如果不符合左旋要求,上一个点出队
// printf("update: segment %d TO %d destination: %d\n",ch.size()-2,ch.size()-1,i);
ch.pop_back();
}
ch.push_back(p[i]);
// printf("ch[ %d ]= %d\n",ch.size()-1,i);
}
if(n>1) ch.pop_back();//起点被重复加入,删去
return ch;
}
//旋转卡壳专题 多边形不能是一条线!
double diameter(Polygon p) { //求凸多边形p的直径(多边形上任意两点间的距离的最大值) 时间复杂度O(n) 注意,p是凸多边形,所以要先求出凸包
int n=p.size(),t=2%n;//易错 n不要设为size-1,否则取模后会漏掉0 比如size=2 n=2 那么t=0 1 2 1 2 漏掉了0
double ans=0.0;
for(int i=0; i<n; i++) {
Line l=Line(p[i],p[(i+1)%n]);//当前边
while(DisPointLine(p[t],l)<=DisPointLine(p[(t+1)%n],l)) { //求使当前边到某点的距离最大的点
t=(t+1)%n;
}
ans=max(ans,max(Distance(p[i],p[t]),Distance(p[(i+1)%n],p[t])));
}
return ans;
}
double convexwidth(Polygon p) { //求凸多边形p的宽度(平行切线间的最小距离) 时间复杂度O(n)
int n=p.size(),t=2%n;//平行线间距可以转化为平行线上一点到线的距离,即点线距
double ans=0.0;//由凸包的性质(没有凹边),我们可以以某边为基础遍历点,距离最大的点一定为凸包的切线,这个点到边的距离即为平行切线间距
for(int i=0; i<n; i++) {
Line l=Line(p[i],p[(i+1)%n]);//当前边
while(DisPointLine(p[t],l)<=DisPointLine(p[(t+1)%n],l)) { //求使当前边到某点的距离最大的点
t=(t+1)%n;
}
ans=max(ans,DisPointLine(p[t],l));
}
return ans;
}
double recArea(Polygon ch) {//最小外接矩形面积 时间复杂度O(N)
int r=2,q=1,p,num=ch.size();//r为底边的对边切点,q为垂直于底边方向最远点,表现为正投影,p为另一侧最远点,表现为负投影
double res=1e10;//易错:q从1开始,因为类似三角形,最大投影就在底边!如果q=2,由于单峰,不可能再取到最大正投影了,同理r不能取0,因为是>而不是>=,r=0或1高为0
for(int i=0; i<num; i++) {
Line l=Line(ch[i],ch[(i+1)%num]);
while(sgn(DisPointLine(ch[(r+1)%num],l)-DisPointLine(ch[r],l))>0) r=(r+1)%num;//寻找最大的高
//i->i+1 点乘 i->q 求投影*底边长 求最大正投影 * 底边长
while(sgn( ((ch[(i+1)%num]-ch[i]) *(ch[(q+1)%num]-ch[i])) - ((ch[(i+1)%num]-ch[i])*(ch[q]-ch[i])) )>0 ) q=(q+1)%num;//寻找投影极值,卡矩形的宽
if(i==0) p=q+1;//凸包投影是单峰函数,递增后必递减或相等(连续等值点最长为2),所以从此开始搜索 +1是为了防止垂直于l的边的两个点
//i->i+1 点乘 i->p 求投影*底边长 求最大负投影 * 底边长
while(sgn( ((ch[(i+1)%num]-ch[i]) *(ch[(p+1)%num]-ch[i])) - ((ch[(i+1)%num]-ch[i])*(ch[p]-ch[i])) )<=0 ) {
p=(p+1)%num;//小于等于为了防止垂直线的两个点
}
double h=DisPointLine(ch[r],l);//以当前边为矩形的高
double w=( ((ch[(i+1)%num]-ch[i])*(ch[q]-ch[i])) - ((ch[(i+1)%num]-ch[i])*(ch[p]-ch[i])) )/Distance(ch[i],ch[(i+1)%num]);//正投影减负投影 得到宽
res=min(res,h*w);
}
return res;
}
double recMeter(Polygon ch) {//最小外接矩形周长 时间复杂度O(N)
int r=2,q=1,p,num=ch.size();//r为底边的对边切点,q为垂直于底边方向最远点,表现为正投影,p为另一侧最远点,表现为负投影
double res=1e10;//易错:q从1开始,因为类似三角形,最大投影就在底边!如果q=2,由于单峰,不可能再取到最大正投影了,同理r不能取0,因为是>而不是>=,r=0或1高为0
for(int i=0; i<num; i++) {
Line l=Line(ch[i],ch[(i+1)%num]);
while(sgn(DisPointLine(ch[(r+1)%num],l)-DisPointLine(ch[r],l))>0) r=(r+1)%num;//寻找最大的高
//i->i+1 点乘 i->q 求投影*底边长 求最大正投影 * 底边长
while(sgn( ((ch[(i+1)%num]-ch[i]) *(ch[(q+1)%num]-ch[i])) - ((ch[(i+1)%num]-ch[i])*(ch[q]-ch[i])) )>0 ) q=(q+1)%num;//寻找投影极值,卡矩形的宽
if(i==0) p=q+1;//凸包投影是单峰函数,递增后必递减或相等(连续等值点最长为2),所以从此开始搜索 +1是为了防止垂直于l的边的两个点
//i->i+1 点乘 i->p 求投影*底边长 求最大负投影 * 底边长
while(sgn( ((ch[(i+1)%num]-ch[i]) *(ch[(p+1)%num]-ch[i])) - ((ch[(i+1)%num]-ch[i])*(ch[p]-ch[i])) )<=0 ) {
p=(p+1)%num;//小于等于为了防止垂直线的两个点
}
double h=DisPointLine(ch[r],l);//以当前边为矩形的高
double w=( ((ch[(i+1)%num]-ch[i])*(ch[q]-ch[i])) - ((ch[(i+1)%num]-ch[i])*(ch[p]-ch[i])) )/Distance(ch[i],ch[(i+1)%num]);//正投影减负投影 得到宽
res=min(res,(h+w)*2);
}
return res;
}
double minspace(Polygon P,Polygon Q) { //凸包最短间距
int yminP=0,ymaxQ=0,n=P.size(),m=Q.size();
for (int i = 0; i < n; i++) if (P[i].y < P[yminP].y) yminP = i; // P上y坐标最小的顶点
for (int i = 0; i < m; i++) if (Q[i].y > Q[ymaxQ].y) ymaxQ = i; // Q上y坐标最大的顶点
P.push_back(P[0]); // 为了方便,避免求余
Q.push_back(Q[0]);
double ans = 0x3f3f3f3f;
for (int i = 0; i < n; i++) {
while( ( (Q[ymaxQ + 1]-P[yminP + 1])^(P[yminP]-P[yminP + 1]) )-( (Q[ymaxQ]-P[yminP + 1])^(P[yminP]-P[yminP + 1]) )>eps ) ymaxQ=(ymaxQ+1)%m;
ans = min(ans, DislineLine(P[yminP], P[yminP + 1], Q[ymaxQ], Q[ymaxQ + 1]));
cout<<"ymin="<< yminP<<" ymax="<<ymaxQ<<" Dis="<<DislineLine(P[yminP], P[yminP + 1], Q[ymaxQ], Q[ymaxQ + 1])<<" ans="<<ans<<endl;
yminP = (yminP + 1) % n;
}
P.pop_back(),Q.pop_back();//多加的起点退掉
return ans;
}
int main() {
return 0;
}
/*
119行求交点的正式代码的解释
S△ACD=(d-a)^(c-a)/2 S△BCD=(c-b)^(d-b)/2
设s1=(d-a)^(c-a) s2=(c-b)^(d-b)
则|AE|/|BF|=s1/s2
由相似得|AO|/|BO|=|AE|/|BF|=s1/s2
|AO|=(s1/s2)|BO|
|AO|/(|AO|+|BO|)=(s1/s2)/[(s1/s2)+1]=s1/s1+s2
则AO=[s1/s1+s2]AB=[s1/(s1+s2)](b-a)
令原点为 O',O'O=O'A+AO
也就是说O的坐标为A的坐标+AO
O=a+(s1/s1+s2)(b-a)
*/
/*
int n;//多边形点的个数
cout<<"请输入多边形1的信息(点数,坐标)"<<endl;
scanf("%d",&n);
Polygon p,ch;//p为多边形,ch为凸包
Point pt;
for(int i=0; i<n; i++) scanf("%lf%lf",&pt.x,&pt.y),p.push_back(pt);
ch=Andrew(p);
printf("凸包的点坐标依次为:\n");//输出凸包
for(int i=0; i<ch.size()-1; i++) printf("(%.0lf,%.0lf) ",ch[i].x,ch[i].y);
printf("(%.0lf,%.0lf)\n",ch[ch.size()-1].x,ch[ch.size()-1].y);
double diam=diameter(ch);
cout<<"凸包直径为"<<diam<<endl;
double width=convexwidth(ch);
cout<<"凸包宽度为"<<width<<endl;
double recarea=recArea(ch);
cout<<"最小包围矩形面积为"<<recarea<<endl;
double recM=recMeter(ch);
cout<<"最小包围矩形周长为"<<recM<<endl;
*/点和向量部分
点和线部分
1.直线的表示
用直线上的两个点表示
struct Line{//直线的表示:线上两个点 Segment线段和直线Line通过typedef共用同一个数据结构
Point p1,p2;
Line(Point a,Point b):p1(a),p2(b){}//不能再写Line(){},因为二义性
};2.线段的表示
#define Segment Line//可以用两个点表示线段,起点是p1,终点是p2。直接用直线的数据结构定义线段3.点和直线的位置关系
在二维平面上点与直线有3种位置关系,即点在直线左侧,在右侧,在直线上。用直线上两点p1,p2与点p构成两个向量,用叉积的正负判断方向,就能得到位置关系。
//点和直线的位置关系 点在直线左边返回1 右边返回2 在直线上返回0
int PointLineRelation(Point p,Line v){//在二维平面上有3种,即点在直线左侧,在右侧,在直线上。用直线上两点p1,p2与点p构成两个向量,用叉积的正负判断方向,就能得到位置关系。
int c=sgn((p-v.p1)^(v.p2-v.p1));//向量p1p 叉乘 p1p2
if(c<0) return 1;
if(c>0) return 2;
return 0;
} 4.点和线段的位置关系
判断点p是否在线段v上,先用叉积判断是否共线,然后用点积看p和v的两个端点产生的角是否为钝角。
//点和线段的位置关系 0为不在线段上,1为在线段上
bool PointOnSeg(Point p,Segment v){//判断点p是否在线段v上,先用叉积判断是否共线,然后用点积看p和v的两个端点产生的角是否为钝角。
return sgn((p-v.p1)^(v.p2-v.p1)) ==0 && sgn((p-v.p1)*(p-v.p2))<=0;
}5.点到直线的距离
已知点p和直线v(p1,p2),求p到v的距离。首先用叉积求p、p1、p2构成的平行四边形的面积,然后用面积除以平行四边形的底边长,也就是线段(p1,p2)的长度,就得到了平行四边形的高,即p点到直线的距离。
//点到直线的距离 已知点p和直线v(p1,p2),求p到v的距离。首先用叉积求p、p1、p2构成的平行四边形的面积 然后用面积除以平行四边形的底边长,也就是线段(p1,p2)的长度,就得到了平行四边形的高,即p点到直线的距离。
double DisPointLine(Point p,Line v){
return fabs((p-v.p1)^(v.p2-v.p1))/Distance(v.p1,v.p2);
}6.两条直线的位置关系
int LineRelation(Line v1,Line v2){//两条直线的位置关系 用两条直线方向向量叉乘来判断 等于0则判断平行还是重合 否则相交 0 平行 1 重合 2 相交
if(sgn((v1.p2-v1.p1)^(v2.p2-v2.p1))==0){
if(PointLineRelation(v1.p1,v2)==0) return 1;//1 重合
else return 0;//0 平行
}
else return 2;//2 相交
}7.求两直线的交点 (叉积公式)

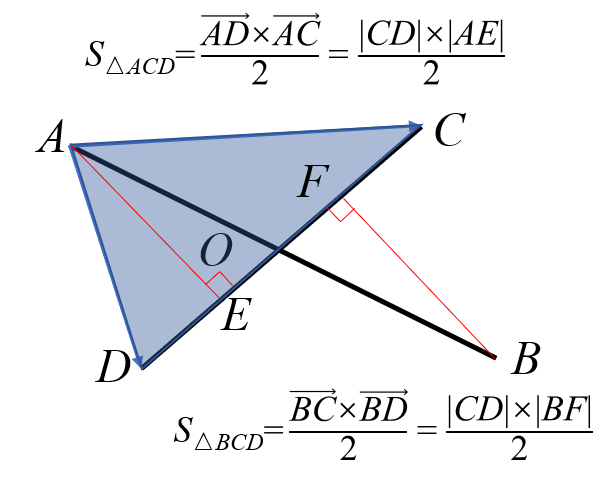

转化为代码思路
S△ACD=(d-a)^(c-a)/2 S△BCD=(c-b)^(d-b)/2
设s1=(d-a)^(c-a) s2=(c-b)^(d-b)
则|AE|/|BF|=s1/s2
由相似得|AO|/|BO|=|AE|/|BF|=s1/s2
|AO|=(s1/s2)|BO|
|AO|/(|AO|+|BO|)=(s1/s2)/[(s1/s2)+1]=s1/s1+s2
则AO=[s1/s1+s2]AB=[s1/(s1+s2)](b-a)
令原点为 O',O'O=O'A+AO
也就是说O的坐标为A的坐标+AO
O=a+(s1/s1+s2)(b-a)
注意两直线不能重合,否则会输出nan,可以用isnan来进行判断和维护鲁棒性
判断是否相交也需要计算,所以我不建议先判断是否相交,这样需要的时间会翻倍,直接判断nan跑得快一些,但是要记得写!
Point CrossPoint(Line l1,Line l2){//两直线交点(叉乘公式) 解释见代码下方注释区 注意两直线不能重合,否则会输出nan,可以用isnan来进行判断和维护鲁棒性
Point a=l1.p1,b=l1.p2,c=l2.p1,d=l2.p2;
double s1=(d-a)^(c-a),s2=(c-b)^(d-b),s=s1/(s1+s2);
Point t=b-a;
return a+t*s;
}8.判断两条线段是否相交
这里仍然利用叉积有正有负的特点。如果一条线段的两端在另一条线段的两侧,那么两个端点与另一线段产生的两个叉积正负相反,也就是说两个叉积相乘为负。如果两条线段互相满足这一点,那么就是相交的。
bool CrossSegment(Line l1,Line l2){//判断两直线是否相交
Point a=l1.p1,b=l1.p2,c=l2.p1,d=l2.p2;//如果一条线段的两端在另一条线段的两侧,那么两个端点与另一线段产生的两个叉积正负相反
double c1=(b-a)^(c-a),c2=(b-a)^(d-a);//也就是说两个叉积相乘为负。如果两条线段互相满足这一点,那么就是相交的
double d1=(d-c)^(a-c),d2=(d-c)^(b-c);//c1=AB^AC c2=AB^AD d1=CD^CA d2=CD^CB
return sgn(c1)*sgn(c2)<0 && sgn(d1)*sgn(d2)<0;
}9.点到直线的投影
Point project(Point p, Segment s) {//求点p在直线s上的投影
Vector base = s.p2 - s.p1;
double r = ( (p - s.p1)* base) / sqrnorm(base);
base = base * r;
return Point(s.p1 + base);
}10.点到线段的距离
inline double DisPointSeg(Point C,Point A, Point B) {//点到线段的距离 计算C点到线段AB的最短距离
if (Distance(A, B) < eps) return Distance(B, C);//AB是同一点
if ((B-A)*(C-A)<-eps) return Distance(A,C);//AB*AC<0 点的投影落在线段之外且与A同侧 支点A离C最近
if ((A-B)*(C-B)<-eps) return Distance(B,C);//BA*BC<0 点的投影落在线段之外且与B同侧 支点B离C最近
Line l=Line(A,B);//点的投影落在线段内,直接计算点线距
return DisPointLine(C,l);
}11.线段间的距离
inline double DislineLine(Point A, Point B, Point C, Point D) {//求线段AB与CD之间的距离(一条线段的两端点到另外一条线段的最小距离),反过来一样,共4种情况
return min( min(DisPointSeg(C,A,B),DisPointSeg(D,A,B)) , min(DisPointSeg(A,C,D),DisPointSeg(B,C,D)) );
}多边形
1.判断点在多边形内部
给定一个点P和一个多边形,判断P是否在多边形内部,有射线法和转角法两种方法。 射线法:从P引一条射线,穿过多边形,如果和多边形的边相交奇数次,说明P在内部;如果是偶数次,说明在外部。
但是射线法有一个限定条件,即多边形必须是一个简单多边形,这个多边形必须是一个简单的闭合曲线所构成的,在多边形所在的平面中只有两个相互分离的部分,即多边形的外部与多边形的内部;且多边形没有自相交与自重叠;
如果出现了复杂的自重叠多边形,在某些多边形二次重叠的部分,射线法并不能很好的判断点是否在多边形内部,此时,就提出了另一种判断方法,转角法。
转角法:把点P和多边形的每个点连接,逐个计算角度,绕多边形一周,看多边形相对于这个点总共转了多少度。如果是360度,说明点在多边形内部,如果是0度,说明点在多边形外;如果是180度说明点在多边形边界上。

但是如果直接计算角度,需要计算反三角函数,不仅速度慢,而且有精度问题。
接下来介绍转角法思想的另一种实现方式:简单来说就是判断,多边形是否对点产生了环绕,累计在计算过程中的环绕数,如果环绕数为0,则在多边形外部,否则在多边形内部;
依然从点引出一条向右的射线,但此时与射线法的区别在于,不再是对与多边形相交数的叠加,而是有加有减的计算;
当射线与方向向上的边相交时,环绕数加一;当射线与方向向下的边相交时,环绕数减一,如图所示,即可更好的判断点是否位于多边形内部。


以点P为起点引一条水平线,检查与多边形每条边的相交情况,例如沿着逆时针,检查P和每个边的相交情况,统计P穿过这些边的次数。c=(P-j)^(i-j) u=i.y-P.y v=j.y-P.y 叉积c用来检查P点在线段ij的左侧还是右侧,u,v用来检查经过P点的水平线是否穿过线段,用num计数。当num>0时,P在多边形内部。其他情况也符合该规律。
i为起点 j为终点 方向逆时针,u为起点与P的纵坐标差值,v为终点与P的纵坐标差值
JP^JI的符号判断左右关系,也可以PJ^IJ,但我们习惯共起点

如果P在ji左边,那么C>0,可能有以下五种情况:

上面是j下面是i,P在ji左边, 则c>0,u<0,j<0,此时环绕数cnt不应该发生变化
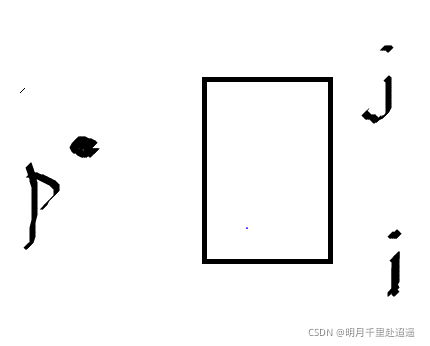
C>0, V>0,U<0,cnt++

P与j所在边平行 C>0 V=0 U<0 cnt++
剩下两种一种是P与i平行,一种是P在下面,就不画了
下面画一幅U或V其中一个等于0仍要计入的原因图
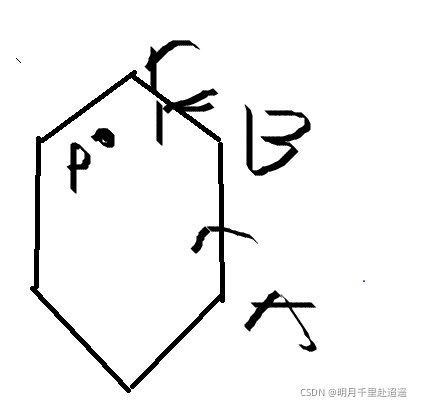
遇到这种情况,我们要让U或V其中一个等于0的也被正确计数,但不能都等于0也计数,否则可能遇到这种情况

很好,思路已经很清晰了

P在IJ右边的情况,C<0,U>0,V<0,cnt++
现在问题是设置U和V哪一个可以小于0?考虑到如果P与端点平行,那么这个端点分列于两条边,一个是起点,一个是终点,也就是说我们设置哪一个都行,但是要考虑到两条边方向相反的情况,那么我们要设置的变量在C的符号不同时也要不同,我们可以这么设置
C>0 U<0 V>=0 cnt++
C<0 U>=0 V<0 cnt--
代码实现
ToLeftTest 判断c是否在ab左边,a->b逆时针方向
bool ToLeftTest(Point c, Point a, Point b) { //逆时针方向的边 a为起点 b为终点 c为边外一点 判断c是否在ab的左边 ab^ac
return ((b-a)^(c-a))>0;
}那么转化为
C==1 U<0 V>=0 cnt++
C==0 U>=0 V<0 cnt--
typedef vector<Point> Polygon;
Polygon Andrew(Polygon p) {//返回凸包
int n=p.size();
sort(p.begin(),p.end());
Polygon ch;//凸包结果
for(int i=0;i<n;i++){ //起点不能出队 所以size>1
while(ch.size()>1 && !ToLeftTest(p[i],ch[ch.size()-2],ch[ch.size()-1])){//下凸包 如果上一条边到这一条边不符合左旋要求,上一个点出队
// printf("update: segment %d TO %d destination: %d\n",ch.size()-2,ch.size()-1,i);
ch.pop_back();
}
ch.push_back(p[i]);//这一个点入队
// printf("ch[ %d ]= %d\n",ch.size()-1,i);
}
int k=ch.size();
for(int i=n-2;i>=0;i--){//从p的倒数第二个点开始,因为下凸包终点是倒数第一个点,倒数第一个点就是上凸包的起点
while(ch.size()>k && !ToLeftTest(p[i],ch[ch.size()-2],ch[ch.size()-1])){ //上凸包 如果不符合左旋要求,上一个点出队
// printf("update: segment %d TO %d destination: %d\n",ch.size()-2,ch.size()-1,i);
ch.pop_back();
}
ch.push_back(p[i]);
// printf("ch[ %d ]= %d\n",ch.size()-1,i);
}
if(n>1) ch.pop_back();//起点被重复加入,删去
return ch;
}2.求多边形的面积


然后依次进行下去

 如果不是按逆时针存储的话,会算出负值,取反就行了
如果不是按逆时针存储的话,会算出负值,取反就行了
一般都是按逆时针存储的
//typedef vector<Point> Polygon;
double Polygon_Area(Polygon p){//求多边形面积,n为多边形顶点数
double area=0;int n=p.size();
for(int i=0;i<n;i++) area+=(p[i]^p[(i+1)%n]);
return fabs(area/2);
}凸包
定义一 (较直观)

定义二
性质
Andrew扫描求凸包
凸包问题是计算几何中的著名问题,有非常广泛的应用。
凸包问题:给定一些点,求能把所有这些点包含在内的面积最小的多边形。
求凸包的算法有两种,一是Graham扫描法,其复杂度是O(nlogn);
二是jarvis步进法,其时间复杂度是O(nh),h是凸包上的顶点数。
这两种算法的基本思路是“旋转扫除”,设定一个参照顶点,逐个旋转到其他所有顶点,并判断这些顶点是否在凸包上。
这里介绍Graham扫描法的变种-Andrew算法,更快更稳定。算法做两次扫描,先从最左边的点沿“下凸包”扫描到最右边,在从最右边的点沿“上凸包”扫描到最左边,“上凸包”和“下凸包”合起来就是完整的凸包。
具体步骤
(1)把所有的点都按照横坐标x从小到大进行排序,如果x相同,按照y从小到大排序,并删除重复的点,得到序列{p0,p1,p2...pm}。
(2)从左到右扫描所有点,求“下凸包”。p0一定在凸包上,它是凸包最左边的顶点,从p0开始,依次检查{p1,p2,...pm},扩展出“下凸包”。判断凸包上点的依据:如果新点在凸包“前进”方向的左边,说明在“下凸包”上,把它加入到凸包,如果在右边,说明拐弯了,删除最近加入的下凸包的点。继续这个过程,直到检查完所有点。拐弯方向用叉积判断即可。






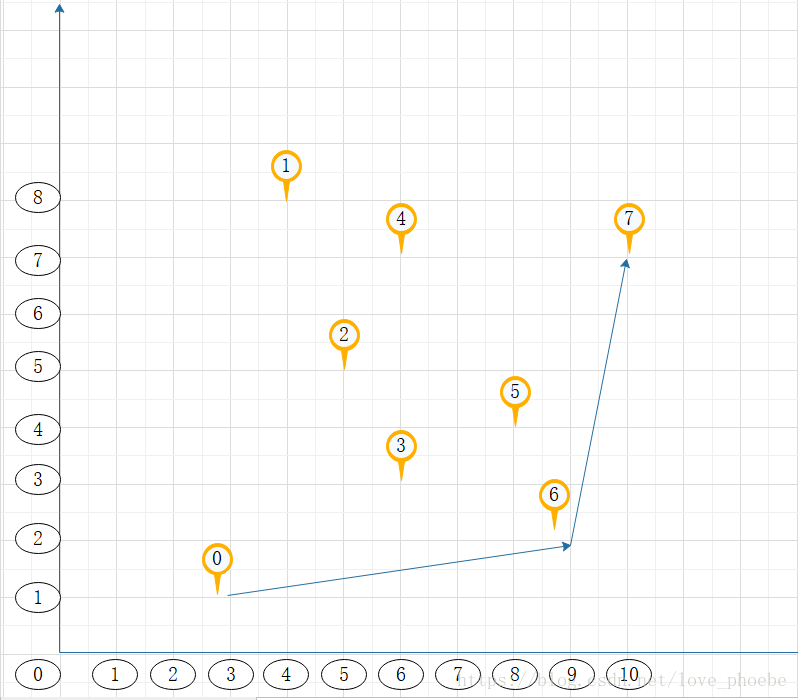






注意上图本身是不符合左旋要求的,4-1这条边就不该出现,1-0是应该出现的,为了过渡原作者还是画上了,不要误解

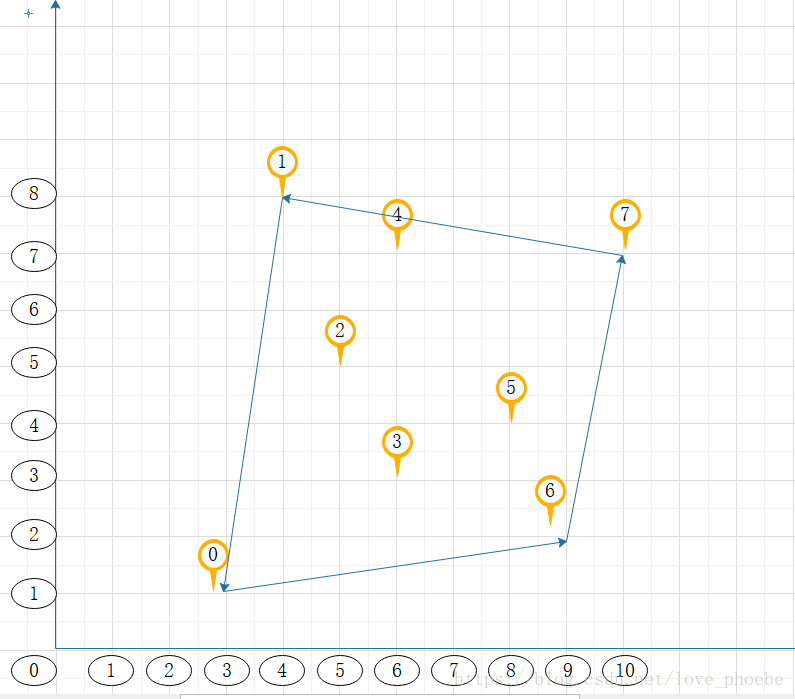
测试数据为图片的数据
测试部分已被注释
Polygon Andrew(Polygon p) {//返回凸包 时间复杂度O(nlogn)
int n=p.size();
sort(p.begin(),p.end());
Polygon ch;//凸包结果
for(int i=0; i<n; i++) { //起点不能出队 所以size>1
while(ch.size()>1 && !ToLeftTest(p[i],ch[ch.size()-2],ch[ch.size()-1])) { //下凸包 如果上一条边到这一条边不符合左旋要求,上一个点出队
// printf("update: segment %d TO %d destination: %d\n",ch.size()-2,ch.size()-1,i);
ch.pop_back();
}
ch.push_back(p[i]);//这一个点入队
// printf("ch[ %d ]= %d\n",ch.size()-1,i);
}
int k=ch.size();
for(int i=n-2; i>=0; i--) { //从p的倒数第二个点开始,因为下凸包终点是倒数第一个点,倒数第一个点就是上凸包的起点
while(ch.size()>k && !ToLeftTest(p[i],ch[ch.size()-2],ch[ch.size()-1])) { //上凸包 如果不符合左旋要求,上一个点出队
// printf("update: segment %d TO %d destination: %d\n",ch.size()-2,ch.size()-1,i);
ch.pop_back();
}
ch.push_back(p[i]);
// printf("ch[ %d ]= %d\n",ch.size()-1,i);
}
if(n>1) ch.pop_back();//起点被重复加入,删去
return ch;
}
int main() {
int n;//多边形点的个数
scanf("%d",&n);
Polygon p,ch;//p为多边形,ch为凸包
Point pt;
for(int i=0; i<n; i++) scanf("%lf%lf",&pt.x,&pt.y),p.push_back(pt);
ch=Andrew(p);
printf("凸包的点坐标依次为:\n");//输出凸包
for(int i=0; i<ch.size()-1; i++) printf("(%.0lf,%.0lf) ",ch[i].x,ch[i].y);
printf("(%.0lf,%.0lf)\n",ch[ch.size()-1].x,ch[ch.size()-1].y);
return 0;
}测试数据
8
3 1
4 8
5 5
6 3
6 7
8 4
9 2
10 7输出结果
ch[ 0 ]= 0
ch[ 1 ]= 1
update: segment 0 TO 1 destination: 2
ch[ 1 ]= 2
update: segment 0 TO 1 destination: 3
ch[ 1 ]= 3
ch[ 2 ]= 4
update: segment 1 TO 2 destination: 5
update: segment 0 TO 1 destination: 5
ch[ 1 ]= 5
update: segment 0 TO 1 destination: 6
ch[ 1 ]= 6
ch[ 2 ]= 7
ch[ 3 ]= 6
update: segment 2 TO 3 destination: 5
ch[ 3 ]= 5
update: segment 2 TO 3 destination: 4
ch[ 3 ]= 4
ch[ 4 ]= 3
update: segment 3 TO 4 destination: 2
ch[ 4 ]= 2
update: segment 3 TO 4 destination: 1
update: segment 2 TO 3 destination: 1
ch[ 3 ]= 1
ch[ 4 ]= 0
凸包的点坐标依次为:
(3,1) (9,2) (10,7) (4,8)旋转卡壳法
凸多边形直径
以下理论知识摘自上面的文章,推荐过去阅读,我截一些关键步骤
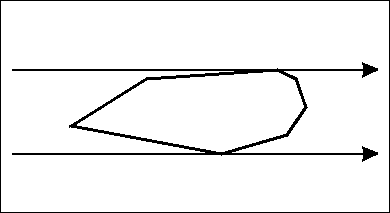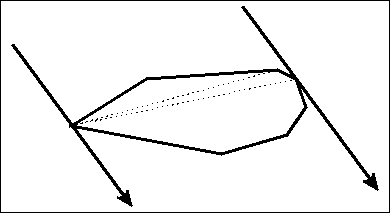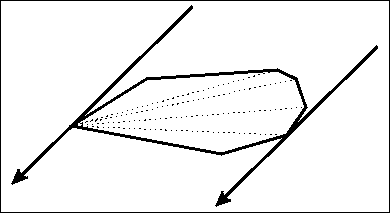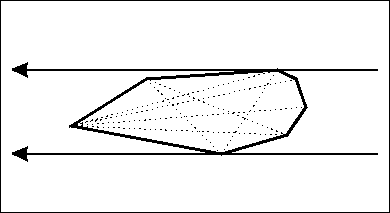
凸多边形的直径即凸多边形上任意两个点之间距离的最大值。直径一定会在对踵点中产生,如果两个点不是对踵点,那么两个点中一定可以让一个点向另一个点的对踵点方向移动使得距离更大。并且点与点之间的距离可以体现为线与线之间的距离,在非对踵点之间构造平行线,一定没有在对踵点构造平行线优,这一点可以通过平移看出。
为了减小误差并方便计算,我们求出每一条边的对踵点。通过上面的图可以看出,边的对踵点同时是这两个点的对踵点,因此并没有遗漏。
同时,通过边来求,可以很好地运用叉积的计算,减小了误差。

对于最下面这条边来说,对于上面四个顶点,他们分别与这条边构成了四个同底不同高的三角形,而三角形面积可以用叉积算出来,三角形的面积此时也就反映了点到直线的距离了。由于面积是单峰的,那么对单独一条边的对踵点,我们可以用三分来求,对于所有边,我们可以用two-pointer来 O(n)求出。因为随着边在逆时针枚举,它的对踵点T也在逆时针移动。
步骤
首先求出凸包,目的是把所有点按逆时针排序。然后枚举逆时针边,定义 T 为当前的对踵点,若 T 逆时针变动能增大到当前边的距离则改变 T,直到继续改变会导致距离减小为止。每次求出边(设为 AB)的对踵点 Ti后,分别用 ∣ATi∣,∣BTi∣ 来更新答案,即凸多边形的直径。
时间复杂度 O(n)。
点到直线的距离
//点到直线的距离 已知点p和直线v(p1,p2),求p到v的距离。首先用叉积求p、p1、p2构成的平行四边形的面积 然后用面积除以平行四边形的底边长,也就是线段(p1,p2)的长度,就得到了平行四边形的高,即p点到直线的距离。
double DisPointLine(Point p,Line v) {
return fabs((p-v.p1)^(v.p2-v.p1))/Distance(v.p1,v.p2);
}代码
double diameter(Polygon p){//求凸多边形p的直径(多边形上任意两点间的距离的最大值) 时间复杂度O(n) 注意,p是凸多边形,所以要先求出凸包
int n=p.size(),t=2%n;//易错 n不要设为size-1,否则取模后会漏掉0 比如size=2 n=2 那么t=0 1 2 1 2 漏掉了0
double ans=0.0;
for(int i=0;i<n;i++){
Line l=Line(p[i],p[(i+1)%n]);//当前边
while(DisPointLine(p[t],l)<=DisPointLine(p[(t+1)%n],l)){
t=(t+1)%n;
}
ans=max(ans,max(Distance(p[i],p[t]),Distance(p[(i+1)%n],p[t])));
}
return ans;
}int main() {
int n;//多边形点的个数
scanf("%d",&n);
Polygon p,ch;//p为多边形,ch为凸包
Point pt;
for(int i=0; i<n; i++) scanf("%lf%lf",&pt.x,&pt.y),p.push_back(pt);
ch=Andrew(p);
printf("凸包的点坐标依次为:\n");//输出凸包
for(int i=0; i<ch.size()-1; i++) printf("(%.0lf,%.0lf) ",ch[i].x,ch[i].y);
printf("(%.0lf,%.0lf)\n",ch[ch.size()-1].x,ch[ch.size()-1].y);
double diam=diameter(ch);
cout<<diam<<endl;
return 0;
}测试数据
8
3 1
4 8
5 5
6 3
6 7
8 4
9 2
10 7测试结果
凸包的点坐标依次为:
(3,1) (9,2) (10,7) (4,8)
9.21954

显然是0-7的距离,根号85=9.21954,验算正确
注意:多边形不能是一条线 如有需要,请提前判断多边形各顶点是否共线,否则会死循环,上面求凸包会从头到尾再到头
凸多边形宽度
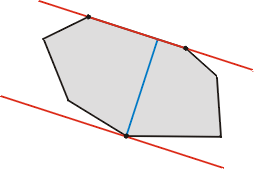
凸多边形的宽度定义为平行切线间的最小距离。
平行线间距可以转化为平行线上一点到线的距离,即点线距
由凸包的性质(没有凹边),我们可以以某边为基础遍历点,距离最大的点一定为凸包的切线,这个点到边的距离即为平行切线间距
相当于上面求直径的求两点间的距离去掉
double convexwidth(Polygon p){//求凸多边形p的宽度(平行切线间的最小距离) 时间复杂度O(n)
int n=p.size(),t=2%n;//平行线间距可以转化为平行线上一点到线的距离,即点线距
double ans=0.0;//由凸包的性质(没有凹边),我们可以以某边为基础遍历点,距离最大的点一定为凸包的切线,这个点到边的距离即为平行切线间距
for(int i=0;i<n;i++){
Line l=Line(p[i],p[(i+1)%n]);//当前边
while(DisPointLine(p[t],l)<=DisPointLine(p[(t+1)%n],l)){//求使当前边到某点的距离最大的点
t=(t+1)%n;
}
ans=max(ans,DisPointLine(p[t],l));
}
return ans;
}
int main() {
int n;//多边形点的个数
scanf("%d",&n);
Polygon p,ch;//p为多边形,ch为凸包
Point pt;
for(int i=0; i<n; i++) scanf("%lf%lf",&pt.x,&pt.y),p.push_back(pt);
ch=Andrew(p);
printf("凸包的点坐标依次为:\n");//输出凸包
for(int i=0; i<ch.size()-1; i++) printf("(%.0lf,%.0lf) ",ch[i].x,ch[i].y);
printf("(%.0lf,%.0lf)\n",ch[ch.size()-1].x,ch[ch.size()-1].y);
double diam=diameter(ch);
cout<<"凸包直径为"<<diam<<endl;
double width=convexwidth(ch);
cout<<"凸包宽度为"<<width<<endl;
return 0;
}测试数据同上
测试结果
凸包的点坐标依次为:
(3,1) (9,2) (10,7) (4,8)
凸包直径为9.21954
凸包宽度为7.06916
最小包围矩形面积和周长
算法思路参考
但是他的代码我看不懂,思考了几天自己写出来了,下面贴一下他的算法思路,代码我就不贴了,有兴趣自己前去阅读

注释比较详细,基本依据上面的代码,关键是求高和宽,高由点到直线距离旋转卡壳求出,宽由投影除以边长旋转卡壳求出,i==0 p=q是因为单峰函数,递增之后必递减,所以省去一些遍历,注释也解释了p=0的后果
所谓旋转卡壳转化为代码就是逆时针遍历,遍历后保留变量,这样就不用每次枚举边就重新遍历n次了。由于凸包的叉乘和点乘是单峰函数,可以预料到对踵点一共遍历n次即可,那么时间复杂度就是O(n)。
double recArea(Polygon ch) {//最小外接矩形面积 时间复杂度O(N)
int r=2,q=1,p,num=ch.size();//r为底边的对边切点,q为垂直于底边方向最远点,表现为正投影,p为另一侧最远点,表现为负投影
double res=1e10;//易错:q从1开始,因为类似三角形,最大投影就在底边!如果q=2,由于单峰,不可能再取到最大正投影了,同理r不能取0,因为是>而不是>=,r=0或1高为0
for(int i=0; i<num; i++) {
Line l=Line(ch[i],ch[(i+1)%num]);
while(sgn(DisPointLine(ch[(r+1)%num],l)-DisPointLine(ch[r],l))>0) r=(r+1)%num;//寻找最大的高
//i->i+1 点乘 i->q 求投影*底边长 求最大正投影 * 底边长
while(sgn( ((ch[(i+1)%num]-ch[i]) *(ch[(q+1)%num]-ch[i])) - ((ch[(i+1)%num]-ch[i])*(ch[q]-ch[i])) )>0 ) q=(q+1)%num;//寻找投影极值,卡矩形的宽
if(i==0) p=q+1;//凸包投影是单峰函数,递增后必递减或相等(连续等值点最长为2),所以从此开始搜索 +1是为了防止垂直于l的边的两个点
//i->i+1 点乘 i->p 求投影*底边长 求最大负投影 * 底边长
while(sgn( ((ch[(i+1)%num]-ch[i]) *(ch[(p+1)%num]-ch[i])) - ((ch[(i+1)%num]-ch[i])*(ch[p]-ch[i])) )<=0 ) {
p=(p+1)%num;//小于等于为了防止垂直线的两个点
}
double h=DisPointLine(ch[r],l);//以当前边为矩形的高
double w=( ((ch[(i+1)%num]-ch[i])*(ch[q]-ch[i])) - ((ch[(i+1)%num]-ch[i])*(ch[p]-ch[i])) )/Distance(ch[i],ch[(i+1)%num]);//正投影减负投影 得到宽
res=min(res,h*w);
}
return res;
}例题HDU 5251 解析https://blog.csdn.net/qq_54886579/article/details/120094083
周长就是(h+w)*2
测试数据同上,输出结果
8
3 1
4 8
5 5
6 3
6 7
8 4
9 2
10 7
凸包的点坐标依次为:
(3,1) (9,2) (10,7) (4,8)
凸包直径为9.21954
凸包宽度为7.06916
最小包围矩形面积为43
最小包围矩形周长为26.3038
多边形间最小距离
例题 POJ3608 传送门
下面适合于凸包彼此不相交不相容的情况
如果遇到相容的题直接求点到边距离最小值就可以了
算法思想参考https://blog.csdn.net/qq_34921856/article/details/80690822


第七点他打错了,应该是最小距离
参考2http://www.hankcs.com/program/algorithm/poj-3608-bridge-across-islands.html
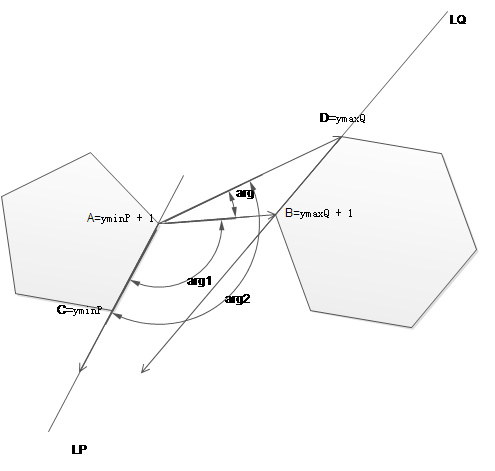
如图所示,AB叉乘AC>AD叉乘AC就把Q上的点后移,也就是
while( ( (Q[ymaxQ + 1]-P[yminP + 1])^(P[yminP]-P[yminP + 1]) )-( (Q[ymaxQ]-P[yminP + 1])^(P[yminP]-P[yminP + 1]) )>eps ) ymaxQ=(ymaxQ+1)%m;
数学意义就是如果AB比AD更近,就把点从D移向B。
举个例子,如图,叉乘是顺时针,得到的值为负值,离得越远绝对值越大,假设AB×AC=-5,AD×AC=-10,-5-(-10)=5>0,Q上的对踵点下移
如果是P下Q上的位置关系的话,双方都是逆时针排列,P向后一位就是往上走,Q向后一位就是往下走,双方会越来越靠近。
如果反过来,P上Q下会怎样?
我们知道,P求的是ymin,Q求的是ymax,如果反过来,那不正好ymin遇到ymax么?然后根据代码,这时候叉乘还是顺时针,还是负值,离得越远绝对值越大,所以循环会让他离的越来越近
inline double DisPointSeg(Point C,Point A, Point B) {//点到线段的距离 计算C点到线段AB的最短距离
if (Distance(A, B) < eps) return Distance(B, C);//AB是同一点
if ((B-A)*(C-A)<-eps) return Distance(A,C);//AB*AC<0 点的投影落在线段之外且与A同侧 支点A离C最近
if ((A-B)*(C-B)<-eps) return Distance(B,C);//BA*BC<0 点的投影落在线段之外且与B同侧 支点B离C最近
Line l=Line(A,B);//点的投影落在线段内,直接计算点线距
return DisPointLine(C,l);
}
inline double DislineLine(Point A, Point B, Point C, Point D) {//求线段AB与CD之间的距离(一条线段的两端点到另外一条线段的最小距离),反过来一样,共4种情况
return min( min(DisPointSeg(C,A,B),DisPointSeg(D,A,B)) , min(DisPointSeg(A,C,D),DisPointSeg(B,C,D)) );
}
typedef vector<Point> Polygon;
double minspace(Polygon P,Polygon Q) { //凸包最短间距
int yminP=0,ymaxQ=0,n=P.size(),m=Q.size();
for (int i = 0; i < n; i++) if (P[i].y < P[yminP].y) yminP = i; // P上y坐标最小的顶点
for (int i = 0; i < m; i++) if (Q[i].y > Q[ymaxQ].y) ymaxQ = i; // Q上y坐标最大的顶点
P.push_back(P[0]); // 为了方便,避免求余
Q.push_back(Q[0]);
double ans = 0x3f3f3f3f;
for (int i = 0; i < n; i++) {
while( ( (Q[ymaxQ + 1]-P[yminP + 1])^(P[yminP]-P[yminP + 1]) )-( (Q[ymaxQ]-P[yminP + 1])^(P[yminP]-P[yminP + 1]) )>eps ) ymaxQ=(ymaxQ+1)%m;
ans = min(ans, DislineLine(P[yminP], P[yminP + 1], Q[ymaxQ], Q[ymaxQ + 1]));
cout<<"ymin="<< yminP<<" ymax="<<ymaxQ<<" Dis="<<DislineLine(P[yminP], P[yminP + 1], Q[ymaxQ], Q[ymaxQ + 1])<<" ans="<<ans<<endl;
yminP = (yminP + 1) % n;
}
P.pop_back(),Q.pop_back();//多加的起点退掉
return ans;
}





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








