0526.优美的排列I

最新推荐文章于 2024-11-04 19:24:37 发布

茶代咖啡

最新推荐文章于 2024-11-04 19:24:37 发布

阅读量168

点赞数

分类专栏： # 算法文章标签：算法 leetcode c++

本文链接：https://blog.csdn.net/qq_55185342/article/details/126782257

版权

算法专栏收录该内容

13 篇文章 1 订阅

订阅专栏

本文探讨了两种方法来解决优美排列问题，即回溯法和动态规划。回溯法通过递归尝试所有可能的数字组合，空间复杂度为O(n^2)，时间复杂度同样为O(n^2)。而动态规划利用状态压缩，以O(2^n)的时间复杂度和O(n)的空间复杂度求解。两种方法均关注于找出能够被索引整除或整除索引的数字的排列组合。

摘要由CSDN通过智能技术生成

1. 题目

2. 解法

2.1 解法一(回溯法)

时间复杂度 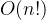$O(n!)$ ,n为排列的长度
空间复杂度 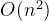$O(n^2)$ ,使用了二维数组
图形化理解:优美的排列
代码

class Solution{
public:
        vector<vector<int>> match;  // 二维数组
        vector<int> vis;    // 标记哪些数被使用过
        int num;    // 最终需要返回的统计结果

        void backtrack(int index, int n) {
            if (index == n+1){  // 如果,数组的空位都被数字填满
                num ++; // 统计结果加一
            }

            for (auto &x: match[index]) {   // 开始对index位置的符合条件的取值进行尝试
                if (!vis[x]) {  // x没有被使用过(vis数组在初始化的时候应该默认为0)
                    vis[x] = true;  // 使用过(表示index防止数x)
                    backtrack(index + 1, n);    // 开始考虑index + 1位置能够进行存储的数据
                    vis[x] = false; // 将该取值恢复至未使用,尝试在index位置进行下一符合条件的取值
                }
            }
        }

        int countArrangement(int n) {
            vis.resize(n + 1);  // 直接进行空间的分配, 避免了索引和i之间需要加一的关系
            match.resize(n + 1);

            for (int i=1; i<=n; i++) {  // 用i表示一维数组的索引

                for (int j=1; j<=n; j++) {  
                    if (i % j == 0 || j % i == 0) { // 将能够被索引整除,或者能够整数索引的数存入索引i对应的行
                        match[i].push_back(j);  
                    }
                }

            }

            backtrack(1, n);    // backtrack(index, n), 表示尝试向位置index放入数, n表示排列的长度
            return num;
        }
};

2.2 解法二(状态压缩动态规划)

时间复杂度 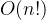$O(n!)$ ,n为排列的长度
空间复杂度 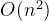$O(n^2)$ ,使用了二维数组
代码

class Solution{
public:
    int countArrangement(int n) {
        // 每个数的选与不选对应1和0两种状态,可以用n位的二进制表示
        // 最终,输出的所有符合情况的数组都对应状态1111

        vector<int> f(1 << n); // 使用一维数组(16个存储空间)作为表

        f[0] = 1;   // 任何一个数字都能单独放在第一位,只有一种放法

        for (int mask = 1; mask < (1 << n); mask++) {   // 对每一个状态都进行讨论

            int num = __builtin_popcount(mask); 
            // 该函数返回二进制状态中1的个数, 也表示当前数组中确定的元素的个数.(num=2, n个元素中,前两个元素在数组中被确定了)

            for (int i = 0; i < n; i++) {

                if (mask & (1 << i) && (num % (i + 1) == 0 || (i + 1) % num == 0)) {
                // 与运算 mask & (1 << i) 表示取mask二进制表示的第i位, 第i位索引位置对应的数字为(i+1)
                // 这个与操作相当于过滤
                // 在内循环中不断增加, 如果mask对应的第i位为0,程序执行就不会进入这个if语句
                // 第i位为0,在下面的转移方程中,执行异或的时候就是0和1异或,结果为1, 但是当前mask的结果f[mask]是不可能通过这样的状态转移过来的

                    f[mask] += f[mask ^ (1 << i)]; // 移位的所有可能情况(1000, 0100, 0010, 0001)
                // mask ^ (1 << i)是将mask的第i位进行取反,第i位为0
                // f(0111)可以从f(0011),f(0101),f(0110)这三个状态转移过来,将它们的方案数进行累加
                }
            
            }

        }
        return f[(1 << n) - 1];
    }
};